matlab内置随机数生成器及随机模拟举例
一、matlab内置的密度函数于随机数生成器
- 离散均匀分布
离散均匀分布用于描述等概率发生事件的状况,仅限于有限的事件数
matlab提供{1,2,…,N}上的均匀分布的概率密度函数黑累计分布函数,其相应的命令为:
unidpdf(X, N): 给出X各个点上的概率值;
unidcdf(X, N): 给出在X个点的累计概率值;
其中矩阵X用于存放各个指定的点。
unidrnd(N): 给出均匀分布于{1, 2, …, N}上的一个随机数;
unidrnd(N, M1, M2)或者unidrnd(N, [M1, M2]):给出由均匀分布于{1, 2, …, N}上的随机数生成的M1xM2矩阵;
如果我们需要每次运行能够产生相同的随机数序列,那么必须控制随机数发生器的种子数,相应的命令为:
s = rng: 获得随机数发生器的中子数,这个命令需要在随机数生成函数之前使用;
rng(s):将随机数发生器的种子数设置为上次使用的种子数s,这样随后的随机数生成函数会产生于前面相同的随机数序列;
rng(‘default’):每次重新运行程序时将获得与上次相同的结果。
rng(‘shuffle’):基于时钟事件来设置随机数发生器的种子数。
hist(data):绘制数据data的直方图;
hist(data, nbins):绘制数据data的直方图,其中nbins用于指定等间隔划分数据的间隔数,nbins默认是10;
hist(data, xcenters): 绘制data的直方图,其中xcenters用于指定划分数据间隔的中心坐标点;
dfittool(data):绘制数据data的pdf赫cdf等图形,这个函数极大地方便了我们识别调查数据所服从的分布类型,对于模拟研究实际系统时它非常有用
均匀分布随机数生成举例:
>> data = unidrnd(6, 1, 5000);
>> hist(data, [1, 2, 3, 4, 5, 6]);
对于一般的离散均匀分布: P ( X = x i ) = 1 / N , i = 1 , ⋯ , N P(X=x_i) = 1/N, i=1,\cdots,N P(X=xi)=1/N,i=1,⋯,N , 我们可以定义一个一一对应的变换函数: h ( i ) = x i , i = 1 , ⋯ , N h(i)=x_i,i=1,\cdots,N h(i)=xi,i=1,⋯,N来产生其随机变量:
X = h ( u n i d r n d ( N ) ) X = h(unidrnd(N)) X=h(unidrnd(N))
- 泊松分布
泊松分布常用来刻画某些随即到达的流量情况,其分布由参数(到达率) λ > 0 \lambda >0 λ>0 决定,其密度分布函数为
P ( k ) = e − λ λ k k ! P(k)=e^{-\lambda}\frac{\lambda^k}{k!} P(k)=e−λk!λk
matlab提供的泊松分布相关的函数为:
poisspdf(X, lambda): 给出变量X各个数时的概率值,其中lambda是泊松分布的参数;
poisscdf(X, lambda): 给出变量X各个数时的累计概率值;
poissrnd(a): 给出服从参数为a的泊松分布的一个随机数;
poissrnd(a, M, N)或者poissrnd(a, [M, N]):给出佛从参数为a的泊松分布的随机数组成的MxN矩阵
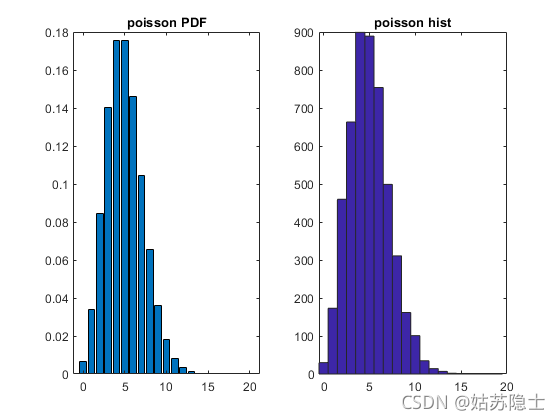
举例:考察 λ = 5 \lambda = 5 λ=5的泊松分布的概率密度,生成随机数统计样本规律
x = 0:20;
lambda = 5;
p = poisspdf(x, lambda);
plot(x, p)
bar(x, p)
subplot(121)
bar(x, p)
title('poisson PDF')
data = poissrnd(lambda, 1, 5000);
subplot(122)
hist(data, [0:19])
title('poisson hist')
- 正态分布
正态分布很常用,因为人们认为很多常见的现象,如误差、干扰或者波动等的变量都服从或者近似服从正态分布。它的分布由期望赫方差两个参数决定,其分布的概率密度函数为
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=σ2π1e−2σ2(x−μ)2
生成正态分布的密度函数以及随机数生成函数命令分别为:
normpdf(X, a, b):给出概率密度函数在X各个点上的值;
normcdf(X, a, b):给出累积分布函数在X各个点上的值;
normrnd(a, b):给出服从期望为a且标准差为b的正态分布的一个随机数;
normrnd(a, b, M, N)或者normrnd(a, b, [M, N]):给出由服从期望为a且标准差为b的正态分布的随机数组成的MxN矩阵
[ahat, bhat] = normfit(data): 给出拟合所估计的正态分布的期望ahat赫标准差bhat,其中data为存放数据的矩阵;
其中a和b分别时分布的期望和标准差,如果缺省这两个参数,则默认a=0,b=1,此时即为标准的正态分布。
举例:我们用300个均匀分布的随机变量之和来逼近正态分布,设 R i U ( − 0.5 , 0.5 ) , i = 1 , ⋯ , 300 R_i ~ U(-0.5, 0.5), i=1,\cdots,300 Ri U(−0.5,0.5),i=1,⋯,300其期望值为0,且方差为 σ 2 = 1 12 \sigma^2=\frac{1}{12} σ2=121
clear all
clf
m = 300;
n = 10000;
nbins = 100;
R = unifrnd(-0.5, 0.5, [m, n]);
Q = sum(R, 1) / 5;
w = (max(Q) - min(Q)) / nbins;
[Y, X] = hist(Q, nbins);
Y = Y / n / w;
t = -3.5:0.05:3.5;
Z = 1 / sqrt(2*pi) * exp(-(t.^2)/2);
hold on
bar(X, Y, 0.5)
plot(t, Z, 'r')
hold off
- 指数分布
当人们考察相继发生事件的时间间隔,或者事件的存续时间,往往发现这些事件的长度时随机的,指数分布常被用来刻画它们。指数概率密度函数为:
f ( x ) = 1 a e − x a , x ≥ 0 f(x)=\frac{1}{a}e^{-\frac{x}{a}},x \ge 0 f(x)=a1e−ax,x≥0
其中参数a>0是分布函数的期望或者标准差,而其倒数 a − 1 a^{-1} a−1则反映单位时间内发生事件的次数,即发生率;
matlab提供的指数分布相关的函数为:
exppdf(X, a): 给出概率密度函数在X各个点上的值;
expcdf(X, a): 给出累积分布函数在X各个点上的值;
exprnd(a):生成服从参数为a的指数分布的随机数;
exprnd(a, [M, N]): 生成由服从指数分布的随机数分布的随机数所生成的MxN矩阵
[ahat] = expfit(data):哟关于指数分布拟合数据data所给出的分布参数ahat
二、随机模拟举例
- 掷硬币
考虑将一枚硬币掷N次,单N很大时,正面出现的几率接近0.5,设计一个随机模拟实验模拟这一现象
% 掷硬币,正面为1, 反面为2,
% 掷N次,统计正面占所有硬币的占比
N = 1000000;
n = 2;
coins = unidrnd(2, N, 1); % 模拟掷硬币过程
pos_coins = sum(coins == 1); % 正面硬币求和
pos_p = pos_coins / N; % 计算正面硬币的占比
fprintf('p = %f\n', pos_p)
| 总掷硬币次数 | 正面次数 | 正面占比 |
|---|---|---|
| 10 | 3 | 0.3 |
| 100 | 41 | 0.41 |
| 1000 | 460 | 0.46 |
| 10000 | 5029 | 0.5029 |
| 100000 | 49950 | 0.499500 |
| 1000000 | 500764 | 0.500764 |
从模拟结果来看,随着N越来越大,正面出现的纪律越来越接近0.5
- 电池问题
我们考虑一个由充电电池构成的供电系统,它是某种便携电子设备的电源。假设共有两个电池和一个充电器,其中仅有一个电池被用来给设备供电,另一个电池备用。由于设备使用的频繁性和不确定性导致耗电量是随机的;设电池耗尽时间等可能是1,2,3,4,5或者6个小时这六种情况之一,即是随机的;而用完的电池从被换下来到充满需要2.5个小时。问该设备能够持续工作的时间?
% 该问题是一个随机模拟问题,随机性的引入过程
% 在于该设备的随机性使用里面,需要统计的使用
% 时长采用多次随机模拟取平均值的方法取得
N = 1000; % 做100次随机试验
t = 0;
for i = 1:N
is_charging = 0;
r = unidrnd(6);
battery_exhaust_time = 0 + r;
s = 2;
time = 0;
full_charge_time = 5000;
while s > 0
time = min(full_charge_time, battery_exhaust_time);
if full_charge_time < battery_exhaust_time
s = s + 1;
if s == 2
full_charge_time = 5000;
continue;
end
end
s = s - 1;
full_charge_time = time + 2.5;
r = unidrnd(6);
battery_exhaust_time = time + r;
end
t = t + time;
end
avg_t = t / N;
fprintf('avg_time = %f\n', avg_t);
平均时长为:avg_time = 13.740000
- 蒙提霍尔问题
这个游戏的玩法是:参赛者面前有三扇关闭的们,其中一扇们后面藏有一辆汽车,而另外两扇门后面则各藏有一只山羊。参赛者从三扇门中随机选取一扇,若选中后面有车的那扇门,可以赢得该汽车。当参赛者选定了一扇门,但尚未开启它的时候,主持人会从剩下两扇门中打开一扇灿友山羊的门,然后问参赛者要不要更换自己的选择,选取另一扇仍然关上的门。这个游戏涉及的问题是:参赛者更换自己的选择是否会降价赢得汽车的机会?
从理论层面分析:参赛者坚持不换,那么他选中汽车的机会为1/3;如果参赛者更换,那么存在两种情况,开始就选中汽车,更换后为汽车的机会为0,开始选中羊,那么更换后肯定是汽车,开始选中羊的机会为2/3,综合起来,参赛者更换赢得汽车的概率更大;接下来用随机模拟的方法来验证这个分析。
% 采用离散均匀分布来进行模拟,[1, 2, 3], 1/2为山羊,3为汽车
% 生成多组随机数,分析结果得出结论
% 1. 不更换的情形,随机数为3,则选中汽车;
N = 1000;
options_no_change = unidrnd(3, N, 1);
car = sum(options_no_change == 3);
p_car_no_change = car / N;
% 2. 更换的情形,随机数为1或者2时,更换后为汽车;
options_change = unidrnd(3, N, 1);
sheep = sum(options_change == 3);
car = N - sheep;
p_car_change = car / N;
fprintf('p_car_no_change = %f, p_car_change = %f\n', p_car_no_change, p_car_change);
采用更换的方式选中汽车的概率为:
| 试验次数 | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
|---|---|---|---|---|---|---|
| 几率 | 0.700000 | 0.720000 | 0.645000 | 0.666300 | 0.663580 | 0.666783 |
- 商品优惠券问题
我们在生活中常常会遇到某些食品商家采用一种游戏方式来提供商品的优惠券。商家在每件商品中附有一张优惠券,每张券上印有一个字,商家要求消费者筹齐所有的字即可享受优惠。现在我们以六个字为例,假如他们是“哥伦比亚咖啡”,并且这六个字的商品是相等数量的,那么,消费者享受到此优惠的可能性有多大呢?显然,买的越多获得优惠的机会越大。我们问:如果消费者购买了12件商品后,能获得优惠的可能性多大?
% 用[1, 2, 3, 4, 5, 6]分别代表“哥伦比亚咖啡”,做1000次独立重复实验,
% 每次独立重复试验为生成12各随机数,统计这12个随机数,若其中同时含有1到6,
% 那么便获得了优惠
N = 1000;
products = unidrnd(6, N, 12);
get_discount = 0;
for i = 1:N
contain_char = 0;
for j = 1:6
if sum(products(i, :) == j) > 0
contain_char = contain_char + 1;
end
end
if contain_char == 6
get_discount = get_discount + 1;
end
end
p_get_discount = get_discount / N;
fprintf('p_get_discount = %f\n', p_get_discount);
统计结果为:0.466000
- 课程选修问题模拟
从某大学今年所有选修过概率论课程的学生当中,随机选出一位。这位学生在该科目取得成绩的概率分布如下表所示:
| 成绩 | A | B | C | D或F |
|---|---|---|---|---|
| 概率 | 0.2 | 0.3 | 0.3 | 0.2 |
模拟该学生参与这门考试获得各个成绩的可能性
% 采用[1, 10]均匀分布来模拟该同学考试的得分,
% 随机数落在[1, 2]得分为A,
% 随机数落在[3, 5]: B
% 随机数落在[6, 8]: C
% 随机数落在[9, 10]: D 或者 E
N = 100000;
scores = unidrnd(10, N, 1);
scoreA = 0;
scoreB = 0;
scoreC = 0;
scoreDE = 0;
for i = 1:N
if scores(i) >= 1 && scores(i) <= 2
scoreA = scoreA + 1;
elseif scores(i) >= 3 && scores(i) <= 5
scoreB = scoreB + 1;
elseif scores(i) >= 6 && scores(i) <= 8
scoreC = scoreC + 1;
elseif scores(i) >= 9 && scores(i) <= 10
scoreDE = scoreDE + 1;
else
end
end
pA = scoreA / N;
pB = scoreB / N;
pC = scoreC / N;
pDE = scoreDE / N;
fprintf('pA = %f, pB = %f, pC = %f, pDE = %f\n', pA, pB, pC, pDE);
统计结果为:
pA = 0.199360, pB = 0.301820, pC = 0.300590, pDE = 0.198230
- 模拟意见调查
一项近期做的意见调查显示,已婚女性中约有70%认为,他们的先生做了至少分内该做的家务。假设这是完全正确的,则加入随机选择一位已婚女性,她认为她的老公有做足够家务的概率是0.7.如果我们个别访问一些女性,就可以假设他们的回答会是互相独立的。我们想要知道,一个100位女性的简单随机样本,会包含至少80位认为老公做了份内家务的女性的概率。通过随机模拟找到100为女性中几位说了老公做了份内的家务。
% 通过[1, 10]均匀分布来模拟女性的回答
% [1, 7]:则做了家务
% [7, 10]:家务不够
personNum = 100;
N = 1000000;
report = unidrnd(10, N, personNum);
doHoursework80 = 0;
doHourseworkHist = zeros(100, 1);
for i = 1:N
iReport = report(i, :);
doHoursework = sum(iReport <= 7);
doHourseworkHist(doHoursework, 1) = doHourseworkHist(doHoursework, 1) + 1;
notDoHousrwork = 100 - doHoursework;
if doHoursework >= 80
doHoursework80 = doHoursework80 + 1;
end
end
p_doHousrwork80 = doHoursework80 / N;
fprintf('p_doHousrwork80 = %f\n', p_doHousrwork80);
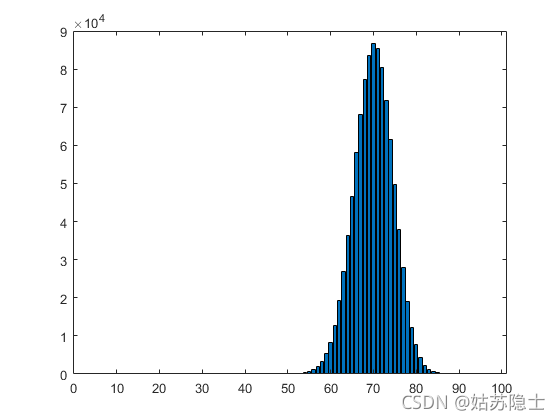
bar(1:100, doHourseworkHist);
统计结果为:p_doHousrwork80 = 0.016569
- 补胎模拟系统
卡车公司每年都要进行大量的轮胎修补工作。在即将到来的一年里,他们预计必须修补2000只瘪胎。瘪胎数随着业务的增长而增加,业务量每年增长20%,且具有标准差为4%的正态分布。目前,司机们都将瘪胎送往最近的服务站修补。今年每只轮胎的平均修补成本是200元,每年的通胀是8%。该公司正在考虑某些选择。一位轮胎商人已向他们提供每只轮胎220元的5年修补合同。而该公司的经理提出,投资500000元购买设备,他们就能在第一年以每只轮胎50元的成本和250000元的固定成本自己修补轮胎。预计公司的成本每年以3%的比率增长。5年后这台设备可以10000元的残值售出。建立模拟模型比较这三种系统,建立美中系统的成本净现值差异。
% 这个问题的随机性体现在瘪胎数量上,先通过随机数发生器模拟出未来五年
% 每年的瘪胎数量,然后对比三种方案的总成本
N = 10000;
cost_sln1 = 0;
cost_sln2 = 0;
cost_sln3 = 0;
% 进行N轮模拟,然后统计平均成本,得出统计规律
for i = 1:N
% 步骤一:未来的瘪胎数量
tyre_num0 = 2000;
tyre_num = zeros(1, 5);
for i_tyre = 1:5
tyre_sigma = 0.04;
tyre_mu = tyre_num0 * (1 + 0.2)^(i_tyre-1);
tyre_num(1, i_tyre) = normrnd(tyre_mu, tyre_sigma, 1, 1);
end
tyre_num = round(tyre_num);
% 方案一的成本
price0 = 200;
for i_year = 1:5
i_price = price0 * (1 + 0.08)^(i_year-1);
cost_sln1 = cost_sln1 + tyre_num(i_year) * i_price;
end
% 方案二的成本
price0 = 220;
for i_year = 1:5
cost_sln2 = cost_sln2 + tyre_num(i_year) * price0;
end
% 方案三的成本
cost_fix = 500000 - 10000;
for i_year = 1:5
i_cost = ( 250000 + 50 * tyre_num(i_year) ) * (1 + 0.03)^(i_year-1);
cost_sln3 = cost_sln3 + i_cost;
end
cost_sln3 = cost_sln3 + cost_fix;
end
% 计算三种方案的平均成本
cost_sln1 = cost_sln1 / N;
cost_sln2 = cost_sln2 / N;
cost_sln3 = cost_sln3 / N;
fprintf('cost_sln1 = %f\n', cost_sln1);
fprintf('cost_sln2 = %f\n', cost_sln2);
fprintf('cost_sln3 = %f\n', cost_sln3);
模拟结果为:
cost_sln1 = 3589348.877824
cost_sln2 = 3274260.000000
cost_sln3 = 2615851.029854
从模拟结果来看,方案三是最节省成本的方案
- 确定概率分布
从均匀分布 U ( 0 , 1 ) U(0, 1) U(0,1)随机地产生N个点,然后排序 X 1 ≤ X 2 ≤ ⋯ ≤ X n X_1 \le X_2 \le \cdots \le X_n X1≤X2≤⋯≤Xn. 设 p i = X i − X i − 1 , i = 2 , 3 , ⋯ , N p_i=X_i-X_{i-1},i=2,3,\cdots,N pi=Xi−Xi−1,i=2,3,⋯,N和 p 1 = 1 + X 1 − X N p_1=1+X_1-X_N p1=1+X1−XN.注意, p i ≥ 0 , p 1 + p 2 + ⋯ + p N = 1 p_i \ge 0, p_1+p_2+\cdots+p_N=1 pi≥0,p1+p2+⋯+pN=1.开始时,取N=4,模拟实验研究 p i p_i pi的分布以及向量 ( p 1 , p 2 , ⋯ , p N ) (p_1,p_2,\cdots,p_N) (p1,p2,⋯,pN)的联合分布。然后尝试考虑N>4的情形。是否所有的 p i p_i pi具有相同的分布?如果是这样,这是什么分布?试问这样的二维随机向量的分布是什么?并回执戚概率魔都函数曲面。
N = 100000;
n = 4; % 这里n为点数
n_points = zeros(N, n);
p_points = zeros(N, n);
for i = 1:N
n_points(i, :) = sort(unifrnd(0, 1, 1, n));
end
p_points(:,1) = 1 + n_points(:, 1) - n_points(:, n);
for i = 2:n
p_points(:, i) = n_points(:, i) - n_points(:, i-1);
end
figure
for i = 1:n
fig_num = sprintf('%d1%d',n,i);
subplot(fig_num);
hist(p_points(:, i));
end
从仿真结果来看,p2,p3,p4的分布近似相同,p1与其他三个相差较远