利用MATLAB可以方便地进行控制系统的时域分析。洋相判断系统的稳定性,只要求出系统的闭环极点,即闭环传递函数的分母多项式的根即可,而分析系统的动态特性,只要求出系统的阶跃响应即可。
利用MATLAB控制系统工具箱中所提供的求联系系统的单位阶跃响应函数step(),单位冲激响应函数impluse(),任意输入信号下的响应函数lsim()等函数可以方便的求出系统在该信号作用下的响应。
step函数(求阶跃响应)
step(num,den)
num表示分子各阶系数,den表示分母各阶系数
作用:已知闭环传递函数,求其阶跃响应
step(num,den)会输出图像;ct2=step(num,den)输出数值。
impulse函数(求脉冲响应)
impulse(num,den)
num表示分子各阶系数,den表示分母各阶系数
作用:已知闭环传递函数,求其脉冲响应
impulse(num,den)会输出图像;ct2=impulse(num,den)输出数值。
lsim函数(求输出)
lsim(sys,u,t)
sys传递函数,u 输入函数,t时域自变量
作用:已知输入函数和传递函数,用这个可以的到每次系统的输入对应的输出(输入函数u要是时域中的,可以输出图像也可以是对应的值)
1.求二阶系统不同阻尼比条件下的阶跃响应曲线
已知典型二阶系统的传递函数为
假设Wn=1,试在同一张图上绘制当阻尼比分别为0、0.1、0.3、0.5、0.7、1、2时系统的单位阶跃曲线
dum=[4]; den1=[1 0 4]; den2=[1 0.4 4]; den3=[1 1.2 4]; en4=[1 2 4]; den5=[1 2.8 4]; den6=[1 4 4]; den7=[1 8 4]; sys1=tf(dum, den1); sys2=tf(dum, den2); sys3=tf(dum, den3); sys4=tf(dum, den4); sys5=tf(dum, den5); sys6=tf(dum, den6); sys7=tf(dum, den7); step(sys1, sys2, sys3, sys4, sys5, sys6, sys7);
可以看到阻尼比为0时无法收敛,其他阻尼比均收敛
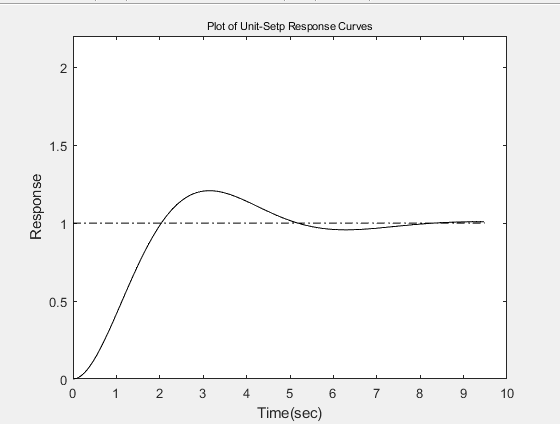
2.求二阶负反馈系统的动态性能指标
设单位负反馈二阶系统的开环传递函数为
G(s)=1.25/s²+s
试计算系统的动态性能指标:上升时间tr、峰值时间tp、超调量、调整时间ts
clear
num=1.25;
den=[1 1 0];
sys=tf(num,den);%建立系统开环传递函数模型
sys=feedback(sys,1);%建立系统闭环传递函数模型
[y,t]=step(sys);%求系统单位阶跃响应
ytr=find(y>=1);
rise_time=t(ytr(1))%计算上升时间
[ymax,tp]=max(y);
peak_time=t(tp)%计算峰值时间
max_overshoot=ymax-1%计算超调量
s=length(t);
while y(s)>0.98&y(s)<1.02
s=s-1;
end
settling_time=t(s+1)%计算调整时间
plot(t,y,'k',t,ones(length(t),1),'k-.')%绘制响应曲线
axis([0 10 0 2.2])
title('Plot of Unit-Setp Response Curves','Position',[5 2.22],'FontSize',8)
xlabel('Time(sec)')
ylabel('Response')
到此这篇关于利用Matlab实现时域分析功能的示例详解的文章就介绍到这了,更多相关Matlab时域分析内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!