数据结构算法之二叉树遍历
二叉树
二叉树是每个结点最多有两个子树的树形结构
通常称为 左子树(left subtree)和右子树(right subtree)
二叉树 通常被称为二叉查找树或二叉堆

一、二叉树遍历是什么?
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
二、为什么研究二叉树的遍历?
因为计算机只会处理线性序列,而我们研究遍历,就是把树中的结点变成某种意义的线性序列,这给程序的实现带来了好处。
三、二叉树的创建
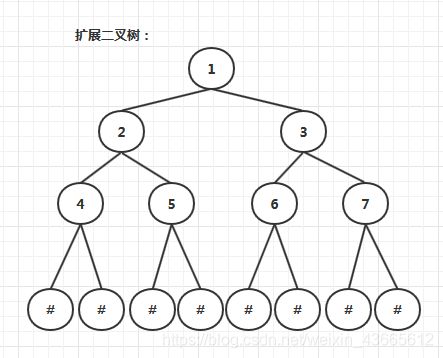
遍历二叉树之前,首先我们要有一个二叉树。要创建一个如下图的二叉树,就要先进行二叉树的扩展,也就是将二叉树每个结点的空指针引出一个虚结点,其值为一个特定值,比如’#’。处理后的二叉树称为原二叉树的扩展二叉树。扩展二叉树的每个遍历序列可以确定一个一颗二叉树,我们采用前序遍历创建二叉树。前序遍历序列:124##5##36##7##。
1.定义二叉链表结点:
// An highlighted block
///
/// 二叉链表结点类
///
///
{
///
/// 数据域
///
public T Data { get; set; }
///
/// 左孩子
///
public TreeNode LChild { get; set; }
///
/// 右孩子
///
public TreeNode RChild { get; set; }
public TreeNode(T val, TreeNode lp, TreeNode rp)
{
Data = val;
LChild = lp;
RChild = rp;
}
public TreeNode(TreeNode lp, TreeNode rp)
{
Data = default(T);
LChild = lp;
RChild = rp;
}
public TreeNode(T val)
{
Data = val;
LChild = null;
RChild = null;
}
public TreeNode()
{
Data = default(T);
LChild = null;
RChild = null;
}
}
2.先序递归创建二叉树:
// An highlighted block
/// 四.二叉树遍历方法
1.前序遍历
递归方式实现前序遍历
具体过程:
1.先访问根节点
2.再序遍历左子树
3.最后序遍历右子树
// An highlighted block
public static void PreOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Console.Write(treeNode.Data);
PreOrderRecur(treeNode.LChild);
PreOrderRecur(treeNode.RChild);
}
非递归方式实现前序遍历
具体过程:
1.首先申请一个新的栈,记为stack;
2.将头结点head压入stack中;
3.每次从stack中弹出栈顶节点,记为cur,然后打印cur值,如果cur右孩子不为空,则将右孩子压入栈中;如果cur的左孩子不为空,将其压入stack中;
4.重复步骤3,直到stack为空.
// An highlighted block
public static void PreOrder(TreeNode<char> head)
{
if (head == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(head);
while (!(stack.Count == 0))
{
TreeNode<char> cur = stack.Pop();
Console.Write(cur.Data);
if (cur.RChild != null)
{
stack.Push(cur.RChild);
}
if (cur.LChild != null)
{
stack.Push(cur.LChild);
}
}
}
模拟:
2.中序遍历
递归方式实现中序遍历
具体过程:
1.先中序遍历左子树
2.再访问根节点
3.最后中序遍历右子树
// An highlighted block
public static void InOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
InOrderRecur(treeNode.LChild);
Console.Write(treeNode.Data);
InOrderRecur(treeNode.RChild);
}
非递归方式实现中序遍历
具体过程:
1.申请一个新栈,记为stack,申请一个变量cur,初始时令cur为头节点;
2.先把cur节点压入栈中,对以cur节点为头的整棵子树来说,依次把整棵树的左子树压入栈中,即不断令cur=cur.left,然后重复步骤2;
3.不断重复步骤2,直到发现cur为空,此时从stack中弹出一个节点记为node,打印node的值,并让cur = node.right,然后继续重复步骤2;
4.当stack为空并且cur为空时结束。
// An highlighted block
public static void InOrder(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
TreeNode<char> cur = treeNode;
while (!(stack.Count == 0) || cur != null)
{
while (cur != null)
{
stack.Push(cur);
cur = cur.LChild;
}
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
cur = node.RChild;
}
}
模拟:
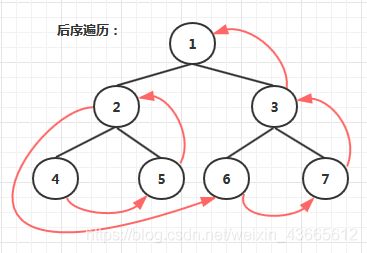
3.后序遍历
递归方式实现中序遍历
具体过程:
1.先后序遍历左子树
2.再后序遍历右子树
3.最后访问根节点
// An highlighted block
public static void PosOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
PosOrderRecur(treeNode.LChild);
PosOrderRecur(treeNode.RChild);
Console.Write(treeNode.Data);
}
非递归方式实现后序遍历一
具体过程:
1.使用两个栈实现
2.申请两个栈stack1,stack2,然后将头结点压入stack1中;
3.从stack1中弹出的节点记为cur,然后先把cur的左孩子压入stack1中,再把cur的右孩子压入stack1中;
4.在整个过程中,每一个从stack1中弹出的节点都放在第二个栈stack2中;
5.不断重复步骤2和步骤3,直到stack1为空,过程停止;
6.从stack2中依次弹出节点并打印,打印的顺序就是后序遍历的顺序;
// An highlighted block
public static void PosOrderOne(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack1 = new Stack<TreeNode<char>>();
Stack<TreeNode<char>> stack2 = new Stack<TreeNode<char>>();
stack1.Push(treeNode);
TreeNode<char> cur = treeNode;
while (!(stack1.Count == 0))
{
cur = stack1.Pop();
if (cur.LChild != null)
{
stack1.Push(cur.LChild);
}
if (cur.RChild != null)
{
stack1.Push(cur.RChild);
}
stack2.Push(cur);
}
while (!(stack2.Count == 0))
{
TreeNode<char> node = stack2.Pop();
Console.WriteLine(node.Data); ;
}
}
非递归方式实现后序遍历二
具体过程:
1.使用一个栈实现
2.申请一个栈stack,将头节点压入stack,同时设置两个变量 h 和 c,在整个流程中,h代表最近一次弹出并打印的节点,c代表当前stack的栈顶 节点,初始时令h为头节点,,c为null;
3.每次令c等于当前stack的栈顶节点,但是不从stack中弹出节点,此时分一下三种情况:
(1)如果c的左孩子不为空,并且h不等于c的左孩子,也不等于c的右孩子,则吧c的左孩子压入stack中
(2)如果情况1不成立,并且c的右孩子不为空,并且h不等于c的右孩子,则把c的右孩子压入stack中;
(3)如果情况1和2不成立,则从stack中弹出c并打印,然后令h等于c;
一直重复步骤2,直到stack为空.
// An highlighted block
public static void PosOrderTwo(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(treeNode);
TreeNode<char> h = treeNode;
TreeNode<char> c = null;
while (!(stack.Count == 0))
{
c = stack.Peek();
//c结点有左孩子 并且 左孩子没被遍历(输出)过 并且 右孩子没被遍历过
if (c.LChild != null && h != c.LChild && h != c.RChild)
stack.Push(c.LChild);
//c结点有右孩子 并且 右孩子没被遍历(输出)过
else if (c.RChild != null && h != c.RChild)
stack.Push(c.RChild);
//c结点没有孩子结点 或者孩子结点已经被遍历(输出)过
else
{
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
h = c;
}
}
}
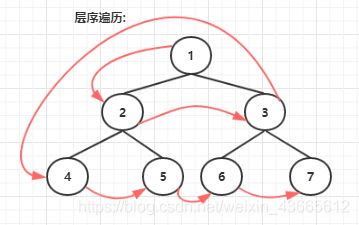
4.层序遍历
1.首先申请一个新的队列,记为queue;
2.将头结点head压入queue中;
3.每次从queue中出队,记为node,然后打印node值,如果node左孩子不为空,则将左孩子入队;如果node的右孩子不为空,则将右孩子入队;
4.重复步骤3,直到queue为空。
// An highlighted block
public static void LevelOrder(TreeNode<char> treeNode)
{
if(treeNode == null)
{
return;
}
Queue<TreeNode<char>> queue = new Queue<TreeNode<char>>();
queue.Enqueue(treeNode);
while (queue.Any())
{
TreeNode<char> node = queue.Dequeue();
Console.Write(node.Data);
if (node.Left != null)
{
queue.Enqueue(node.Left);
}
if (node.Right != null)
{
queue.Enqueue(node.Right);
}
}
}
总结(可以不看 个人理解)
所谓遍历简单的讲就好比在迷宫中寻宝,宝物就藏在某一个树节点当中,但我们并不知道具体在哪个节点上,因此要找到宝物就需要将全部的树节点系统性的搜索一遍。
那么该怎么系统性的搜索一遍二叉树呢?
给定一个单链表你几乎不需要思考就能知道该如何遍历,很简单,拿到头节点后处理当前节点,然后拿到头节点的下一个节点(next)重复上述过程直到节点为空。
你会看到遍历链表的规则很简单,原因就在于链表本身足够简单,就是一条线,但是二叉树不一样,二叉树不是一条简单的"线",而是一张三角形的"网"。
我们可以一层一层的搜索,依次从左到右遍历每一层节点,直到当前层没有节点为止,这是二叉树的一种遍历方法。树的这种层级遍历方法利用了树的深度这一信息(相对于根节点来说),同一层的节点其深度相同,那么我们是不是可以利用树有左右子树这一特点来进行遍历呢?答案是肯定的。
如上图所示1的左子树是2,2的左子树是3,2的右子树是4。。。
假设我们首先遍历根节点1,然后呢,你可能会想然后遍历2的左子树吧,也就是2,当我们到了2这个节点之后再怎么办呢?要遍历2的右子树吗?显然我们不应该去遍历2的右子树,为什么?原因很简单,因为从节点1到节点2我们是沿着左子树的方向来遍历的,我们没有理由到节点2的时候改变这一规则,接下来我们继续沿用这一规则,也就是首先遍历左子树。
我们来到了节点3,节点3的左子树为空,因此无需遍历,然后呢?显然我们应该遍历节点3的右子树,但是3的右子树也为空,这时以3为根节点的树全部遍历完毕。
当遍历完节点3后该怎么办呢?如果你在迷宫中位于节点3,此时节点3已经是死胡同了,因此你需要做的就是沿着来时的路原路返回,回退到上一个节点也就是3的父节点2,这在计算机算法中被称为回溯,这是系统性搜索过程中常见的操作,回到2后我们发现2的左子树已经搜索完毕,因此接下来需要搜索的就是2的右子树也就是节点4,因为节点4还没有被搜索过,当来到节点4后我们可以继续使用上述规则直到这颗树种所有的节点搜索完毕为止,为什么到节点4的时候可以继续沿用之前的规则,原因很简单,因为以4为根节点的子树本身也是一棵树,因此上述规则同样适用。