Pytorch : 自动求导

在训练神经网络时，最常用的算法是反向传播算法。在该算法中，参数(模型权重)根据损失函数相对于给定参数的梯度进行调整。损失函数计算神经网络产生的期望输出和实际输出之间的差值。目标是使损失函数的结果尽可能接近于零。该算法通过网络反向遍历来调整权重和偏差，以重新训练模型。这就是为什么它被称为反向传播。
为了计算这些梯度，PyTorch有一个内置的微分引擎torch.autograd。它支持任何计算图的梯度自动计算。

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

Tensors, Functions and Computational graph

上面的代码定义的计算图如下：

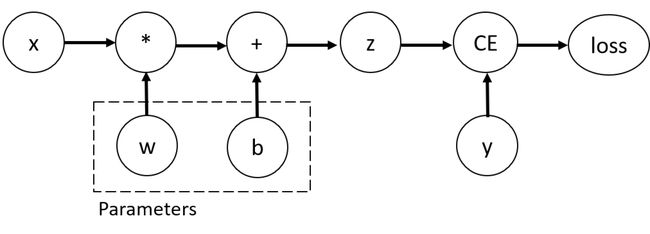
在这个网络中，w和b是我们需要优化的参数。因此，我们需要能够计算损失函数关于这些变量的的梯度。为了做到这一点，我们设置了这些张量的requires_grad性质。

Note: 你可以在创建一个张量时设置require_grad的值，或者稍后使用x.requires_grad_(True)方法

构造计算图的作用于tensors上的函数实际上是Function类的一个对象。该对象知道如何正向计算函数值，以及如何在反向传播步骤中计算其导数。对反向传播函数的引用存储在tensor的grad _fn属性中
为了优化神经网络中参数的权重，我们需要计算损失函数对参数的导数，在x和y的固定值下，我们需要计算$\frac{\partial \mathrm{loss}}{\partial \mathrm{w}},\frac{\partial \mathrm{loss}}{\partial \mathrm{b}}$。为了计算这些导数，我们调用loss.backward()，然后从w.grad和b.grad中获取。

我们只能获得计算图的叶节点的grad属性，这些叶节点需要设置requires_grad属性为true。对于我们图中的其他节点，梯度将不可获得。此外，出于性能原因，我们只能在给定图上使用一次backward()进行梯度计算。如果我们需要在同一图上进行几次反向传播，则需要在调用backward时设置retain_graph = True。

Disabling gradient tracking

当我们不需要反向传播计算梯度时，可以使用torch.no_grad()函数停止跟踪计算梯度。

# python代码
z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w)+b
print(z.requires_grad)

//等效的C++代码
z = torch::matmul(x, w) + b;
std::cout << z.requires_grad() << std::endl;

{
    torch::NoGradGuard no_grad;
    z = torch::matmul(x, w) + b;
}
std::cout << z.requires_grad() << std::endl;

对于PyTorch的C++库LibTorch，torch.no_grad在PyTorch的Python API中的等效物是torch::NoGradGuard no_grad。这是一个RAII线程本地守卫，用于在C++中禁用梯度计算。与Python的实现类似，通过实例化torch::NoGradGuard类的对象可以禁用LibTorch中的梯度计算。在此模式下，每个计算的结果都将具有requires_grad=false。

实现相同效果的另一种方法是在张量上使用detach()方法

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

从概念上讲，autograd用由Function对象组成的有向无环图(DAG)记录数据(张量)和所有执行的操作(以及由此产生的新张量)。在这个DAG中，叶是输入张量，根是输出张量。通过从根到叶跟踪这个图，您可以使用链式法则自动计算梯度。

使用backward()函数反向传播计算tensor的梯度时，并不计算所有tensor的梯度，而是只计算满足这几个条件的tensor的梯度：

1. 类型为叶子节点
2. requires_grad=True
3. 依赖该tensor的所有tensor的requires_grad=True

所有满足条件的变量梯度会自动保存到对应的grad属性里。

Tensor gradients and Jacobian products

Python API

torch.autograd.grad(outputs, inputs, 
					grad_outputs=None, 
					retain_graph=None, 
					create_graph=False, 
					allow_unused=False, 
					is_grads_batched=False)

C++API

using namespace torch::autograd;
using torch::autograd::variable_list = std::vector<Variable>;
using torch::autograd::Variable = at::Tensor;
//variable_list就是std::vector
variable_list torch::autograd::grad
(const variable_list &outputs, 
 const variable_list &inputs, 
 const variable_list &grad_outputs = {}, 
 c10::optional<bool> retain_graph = c10::nullopt, 
 bool create_graph = false, bool allow_unused = false)

计算并返回输出对输入的梯度。

• outputs: 可微函数的输出
• inputs: 输入，计算的输出相对于输入的梯度(不会积累到at::Tensor::grad).
• grad_outputs: Jacobian-vector乘积中的向量。通常是相对于每个输出的预先计算的梯度。标量Tensors 或者不需要计算梯度的张量可以设置为torch::Tensor().
• retain_graph: 如果为false，则用于计算grad的图形将被释放。请注意，在几乎所有情况下，将此选项设置为true是不必要的，而且通常可以以更高效的方式解决。默认值为create_graph的值。
• create_graph: 如果为真，则将构建导数图，从而允许计算更高阶导数乘积。默认值为：false。
• allow_unused: 如果设置为false，则在计算输出与输入无关（因此它们的梯度始终为零），则报错。默认为false。
• is_grads_batched: 目前为python特有参数。如果为True, grad_output的第一个维度将被解释为批处理维度。我们不再计算单个的向量-雅可比矩阵积，而是为批中的每个向量计算一批向量-雅可比矩阵积。我们使用vmap原型特性作为后端来向量化对autograd引擎的调用，这样计算就可以在单个调用中执行。与手动循环和多次向后执行相比，这应该会导致性能改进。

函数行为

输入$m$ 个输入向量$x_i$ , $n$ 个输出向量 $y_j$以及 以及 $n$ 个权重向量$v_j$（形状与对应 $y_j$一致），函数会输出 $m$ 个向量的元组 $(g_1,g_2,\cdots ,g_m)$，细节为 :
输入：$x_i,y_j,v_j;i=1,\cdots ,m,j=1,\cdots ,n;y_j,v_j$形状一致
令$$y=\sum _{j=1}^n{v}_j\cdot y_j$$
其中$(\cdot )$ 为向量内积运算
对任意$i\in \{1,2,\dots ,m\}$，记$x_i=(x_{i_1},x_{i_2},\dots ,x_{i_{k_i}})$，则$g_i=\left(\frac{\partial y}{\partial x_{i_1}},\dots ,\frac{\partial y}{\partial x_{i_{k_i}}}\right)$
输出元组$\mathbf{g}=(g_1,g_2,\dots ,g_m)$
文字描述一下，也就是说，首先程序会将 $v_j$ 与 $y_j$ 两两做内积然后相加，得到合并的标量输出 $y$，然后对每一个 $x_i$ 的每一个分量 $x_{i_s}$（$s=1,2,\cdots ,k_i$），计算 $y$对 $x_{i_s}$ 的偏导数，最后把 $\frac{\partial y}{\partial x_{i_s}}$ 组装成 $g_i$；最后 $m$ 个 输入向量 $x_i$ 对应 $m$ 个梯度$g_i$，合并成一个元组（C++中是一个vector）后返回。

注意： 再扩展一下，输入$x_i$和输出$y_j$及权重$v_j$可以不是向量，而是更高维度的张量，这时$v_j$与$y_j$之间就变成了张量点乘 （即对应元素相乘再求和得到一个标量），无论如何最终是将输出转化为一个标量再对输入求导，所以求导的结果与输入尺寸相同。

参数要求：

1. 任意 $x_i$， 都需要执行 xi.requires_grad_()
2. 任意 $x_i$，需存在 $y_j$，使得 $x_i$ 参与了 $y_j$ 的计算，否则需要设置 allow_unused=True 才不会报错，此时输出的对应 $g_i$ 为 None。
3. 任意 $y_i$，对应一个 $v_i$，两者形状需相同。当 $y_i$ 为标量时，$v_i$ 可以为 None（C++中为torch::Tensor()），此时 $v_i$ 自动取 1.0；当所有的 $y_i$ 均为标量时，grad_outputs 可以取 None（C++中为torch::Tensor()，这也是其默认值），此时 grad_outputs 自动取 n个1.0。 值得注意的是，实际测试下 grad_outputs 可以输入超过 n 个 v_i，但是多出来的会直接忽略。
4. 函数执行一遍后若再次对 $y_i$ 求偏导会报错，因为执行一遍后会删除计算图，除非设置 retain_graph=True。
5. 若之后想求 $g_i$ 对 $x_i$ 的偏导（也就是高阶导）会报错，因为 $g_i$ 没有 连接 $x_i$ 的计算图，除非设置 create_graph=True（此时 retain_graph=create_graph=True）
6. is_grads_batched 默认为 False，若设置为 True 则允许批操作（C++中无此参数，没有批模式），详解如下：
   输入：$y_j,x_i,{\mathbf{V}}_j;i=1,\dots ,m;j=1,\dots ,n;$ 此时${\mathbf{V}}_j$的首个维度代表批数量，$y_j$与${\mathbf{V}}_j$第一维的每个元素形状一致。
   记 y ⃗ i = ( y i 1 , y i 2 , … , y i p ) , V i = ( v i 11 ⋯ v i 1 p ⋮ ⋱ ⋮ v i N 1 … v i N p ) \vec{y}_i=(y_{i_1},y_{i_2},\dots,y_{i_p}),\textbf{V}_i=\begin{pmatrix}v_{i_{11}}&\cdots&v_{i_{1p}}\\ \vdots&\ddots&\vdots\\ v_{i_{N1}}&\dots&v_{i_{Np}}\end{pmatrix} y ​i​=(yi1​​,yi2​​,…,yip​​),Vi​= ​vi11​​⋮viN1​​​⋯⋱…​vi1p​​⋮viNp​​​ ​
   令 y ⃗ = ∑ i = 1 m ( V i [ 1 ] ⋅ y ⃗ i ⋮ V i [ j ] ⋅ y ⃗ i ⋮ V i [ n ] ⋅ y ⃗ i ) ,   ( ⋅ ) \vec{y}=\sum \limits_{i=1}^m \begin{pmatrix} \mathbf{V}_i[1]\cdot\vec{y}_i\\ \vdots\\ \mathbf{V}_i[j]\cdot\vec{y}_i\\ \vdots\\ \mathbf{V}_i[n]\cdot\vec{y}_i \end{pmatrix},\ (\cdot) y ​=i=1∑m​ ​Vi​[1]⋅y ​i​⋮Vi​[j]⋅y ​i​⋮Vi​[n]⋅y ​i​​ ​, (⋅)为点乘运算，同样适用于高维张量（张量点乘：对应元素相乘再求和）
   对任意$i\in \{1,2,\dots ,m\}$
   记$x_i=(x_{i_1},x_{i_2},\cdots ,x_{i_s})$
   则 g ⃗ i = ∇ x ⃗ i y ⃗ = ( ∂ y 1 ∂ x i 1 ⋯ ∂ y i ∂ x i s ⋮ ⋱ ⋮ ∂ y p ∂ x i 1 ⃗ ⋯ ∂ y p ∂ x i s ⃗ ) \vec{g}_i=\nabla_{\vec{x}_i}\vec{y}=\begin{pmatrix}\dfrac{\partial y_1}{\partial x_{i_1}}&\cdots&\dfrac{\partial y_i}{\partial x_{i_s}}\\ \vdots&\ddots&\vdots\\ \dfrac{\partial y_p}{\partial\vec{x_{i_1}}}&\cdots&\dfrac{\partial y_p}{\partial\vec{x_{i_s}}}\end{pmatrix} g ​i​=∇x i​​y ​= ​∂xi1​​∂y1​​⋮∂xi1​​ ​∂yp​​​⋯⋱⋯​∂xis​​∂yi​​⋮∂xis​​ ​∂yp​​​ ​
   输出$\mathbf{g}=(g_1,g_2,\dots ,g_m)$

注意： C++API没有批模式，但是权重可以是输出的倍数(grad_output shape compatible with output)
例如，output.shape = {2,3} , grad_output.shape = {4,3} 或 grad_output.shape = {2,2,3} 结果会按照output的尺寸分割grad_output，并分批进行张量点乘再求和得到一个标量，最终返回标量对于输入的导数。

pytorch允许计算 Jacobian product而非Jacobian矩阵

对于一个向量函数 $y=f(x)$， 其中$x=⟨x_1,\dots ,x_n⟩,y=⟨y_1,\dots ,y_m⟩$，$y$关于$x$ 的导数即Jacobianmatrix, $J_{ij}=\frac{\partial y_i}{\partial x_j}$.

不计算Jacobian matrix本身，Pytorch允许计算Jacobian matrix和一个给定的输入向量$v=(v_1\dots v_m)$的乘积$v^T\cdot J$.要实现这个功能只需在调用backward时将向量$v$作为参数传递即可。向量$v$的维度应该和原始张量相同。

inp = torch.eye(5, requires_grad=True)
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp), retain_graph=True)
print("First call\n", inp.grad)
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nSecond call\n", inp.grad)
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nCall after zeroing gradients\n", inp.grad)

注意，当我们用相同的参数第二次反向调用时，梯度的值是不同的。这是因为在进行反向传播时，PyTorch会累积梯度，即计算梯度的值被添加到计算图的所有叶节点的grad属性中。如果你想计算合适的梯度，你需要在之前将梯度属性归零。在现实训练中，优化器自动帮助我们做到这一点。