数字逻辑 02.逻辑代数基础
基础：
逻辑函数基本概念：
01.逻辑代数的定义：又叫做布尔代数，用一个L表示，是一个封闭的代数系统。由01.常量0和1，02.逻辑变量集k和03.**三种基本运算“与，或，非”**组成
02.逻辑公理：
03.逻辑变量：用字母表示其值可以变换的量，取值只有0或者1。
04.或运算：决定某一个事件是否发生的多个条件中，只要一个条件或者一个以上成立，事件就会成立。运算符号用“+”或者“v”表示
| 或运算 | 条件A | 条件B | 结果F |
|---|---|---|---|
| A+B | 0 | 0 | 0 |
| A+B | 1 | 0 | 1 |
| A+B | 0 | 1 | 1 |
| A+B | 1 | 1 | 1 |
实现或运算的逻辑电路叫做“或门”
05.与运算：决定一个事件发生的多个条件都成立，这个事件才会发生。运算符号用“^”表示
| 与运算 | 条件A | 条件B | 结果F |
|---|---|---|---|
| A^B | 0 | 0 | 0 |
| A^B | 1 | 0 | 0 |
| A^B | 0 | 1 | 0 |
| A^B | 1 | 1 | 1 |
数字电路中实现与运算功能的电路叫做“与门”
06.非运算：某一个事件的发生取决于条件的否定，只有条件不成立，事件才可以发生。运算符号是在逻辑变量上加一横线或者“┐”。
| 非运算 | 条件A | 结果F |
|---|---|---|
| ┐ A | 0 | 1 |
| ┐ A | 1 | 0 |
实现非运算的电路叫做非门或者叫做“反相器”：
函数：随着自变量变化的因变量
逻辑函数：跟一般的函数不一样的地方在于：01.跟逻辑变量一样，取值只有0或者1。随着逻辑变量的改变而改变。02.函数跟变量之间的关系由“与，或，非”三种基本运算决定。
电路表示的逻辑函数：
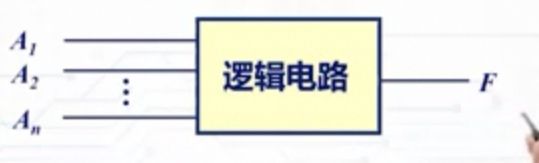
A1,A2,A3,An是逻辑变量，对于每一个确定的逻辑变量A1，A2,A3…An，都有唯一确定的F相对应，这个时候F就是逻辑函数。记为：F=f（A1，A2,A3…An）。
逻辑函数的基本定理和规则：
基本定理：
定理1：
0+1=1 1+1=0 0+0=0 1+0=1
0^0=0 0^1=0 1^0=0 1^1=1
定理2：
A+A=A A^A=A
定理3：
A+(A^B)=A
A^(A+B)=A
定理4：
A+(┐A^B)=A+B
A ^ (┐A+B)=A^B
定理5：
┐(┐A)=A
定理6：
┐(A+B)=┐A^┐B
┐(A^B)=┐A+┐B
定理7：
(A^ ┐ B)+(A^B)=A
(A+B)^(A+┐B)=A
一直到定理7
重要规则：
代入规则：
任意一个存在逻辑变量A的等式，把所有A出现过的位置换成一个相同的逻辑函数F，等式依旧成立。（这不就是黑盒试验吗）
反演规则：
在逻辑函数F中，怎么求┐F这个逻辑函数F的反函数呢？
运算：或运算（v、+）变成与运算（. 、^），与运算变成或运算。
变量：如果直接存在0，1变量，把0变成1，把1变成0。如果是逻辑变量A这种情况，A变成┐A。
运算顺序：先后保持不变。
对偶规则：
对偶式：在逻辑函数F中，如果
01.修改运算，将或运算改成与运算，将与运算变成或运算
02.修改01变量，如果直接存在这种0或者1的变量的话，0改成 1，1改成0
03.保持运算顺序不变
得到F‘逻辑函数，这个F‘函数就叫做逻辑函数F的对偶式。
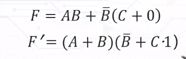
如果两个函数F和G相等，那么他们的对偶函数F‘和G‘也是相等的。
复合逻辑：
逻辑代数的基本运算是与或非三种情况。但是实际上，运算有时候会结合起来。通常有“与非”，“或非”，“与或非”，“异或”
与非逻辑：
是通过与和非两种逻辑形成的，用逻辑函数F表示：
性质：
01.只要其中一个逻辑变量取值是0，结果是1
02.只有逻辑变量全部为1的时候，结果是0
或非逻辑：
是由或和非两种逻辑组成的，用逻辑函数F表示为：
性质：
01.只要逻辑变量中存在一个取值为 1，结果取值是0
02.必须全体逻辑变量取值均是0，结果取值是1
与或非逻辑：
是 由与或非三种逻辑组成，逻辑函数F表示为：
性质：
每个与项，都是0的时候，才会是结果取1
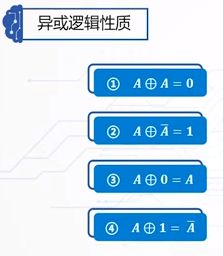
异或逻辑：
这个是一种特别的逻辑，现阶段用于奇偶校验。逻辑函数F的表示为：
性质：
01.当A与B取值相同的时候，F的值是0
02.当A与B取值不同（一个是0，一个是1），F的值是1
同或逻辑;
这个也是一个特殊的逻辑，用逻辑函数F表示：
性质;
01.A与B取值相同，结果是1
02.A与B取值相反，结果是0
逻辑函数的表达式的形式和变换：
- 基本形式：任何一个逻辑函数的形式都不是唯一的，但是我们可以把他们变成两种基本的表达式。一种是与-或表达式，另一种是或-与表达式。
与-或表达式：**由若干“与项”进行或运算得到的。**基本的与项可以是单一逻辑变量，或者是单一逻辑反变量，或者是多个逻辑变量（也包括反变量）进行与运算组成的项
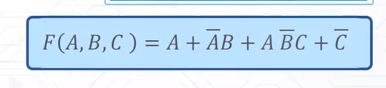
与项===积项，与-或表达式看上去就像是乘积求和
或-与表达式：跟上面的与-或表达式差不多，基本项是或项。或项可以是单一的逻辑变量，或者单一的反变量，或者是多个逻辑变量进行或运算组成的项。
或项==和项。或-与表达式看上去就像是一个因式分解完成的乘积
- 最小项和最大项
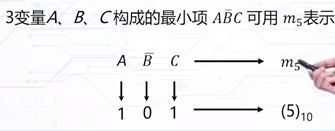
最小项（标准与项）：01.具有n个变量的函数的与项，包含全部的n变量。 02.每个变量以原变量或者反变量出现一次，就不会在出现了。
最小项的数目：
最小项的表示：mi，其中i代表着下标。
用最小项表示逻辑函数：
最大项：01.具有n个变量的函数的或项，包含全部的n变量。 02.每个变量以原变量或者反变量出现一次，就不会在出现了。
最大项数目：2^n
最大项表示形式：Mi。i的值是下标的，
标准形式：就是单纯由与-或表达式（与项都是最小项）或者是或-与表达式（或项都是最大项）。
3.如何从一般的形式变成标准形式
01.代数转换法：
转换成为与-或表达式:
第一步：将一般形式转换成为与-或表达式
第二步：在那些不是最小项 的与项中，反复使用X=X（Y+┐Y），将这些不是最小项的与项转换成为最小项
转换成为或-与表达式：
第一步：将一般形式转换成为或-与表达式
第二步：在那些不是最大项 的或项中，反复使用
公理7X=(X+Y)^(X+┐Y)，把那些不是最大项的项转换成为最大项。
02.真值表转换法：
与-或表达式转换成最小项：
标准是找到k组组合值是1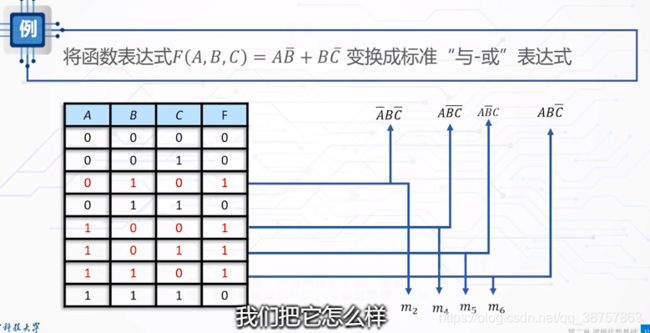
或-与表达式转换成为最大项：
找到k组组合值是0
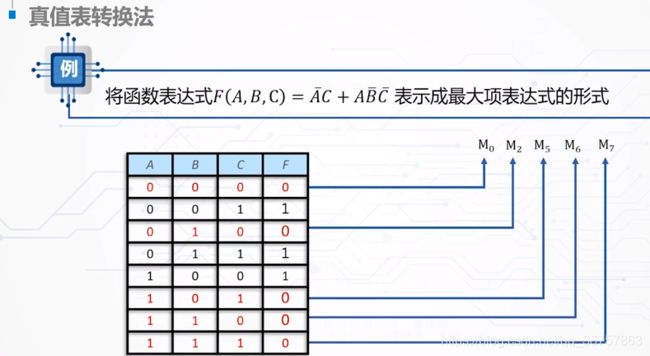
逻辑函数的化简（与 -或表达式，或-与表达式的化简）：
化简逻辑函数，是为了实现电路的更简化设计。化简的起点是：与-或表达式 或-与表达式 这两种。
化简的方法：01.代数化简法，利用逻辑代数中的公理和定理，规则化简逻辑函数
02.卡若图的化简法 03.列表化简法
01.代数化简法：
主要看与-或表达式化简，什么是最简表达式？
为什么要这样呢？
与-或表达式的化简：
01.并项法：利用定理7中(A^ ┐ B)+(A^B)=A，将两个与项合并成一个与项
02.吸收法：利用定理3中的A+AB=A，吸收一个与项。
03.消去法：利用定理4的A+(┐A^B)=A+B，消去与项的一个逻辑变量
04.配项法：利用公理4和公理5中的A^1=A A+（┐A）=1
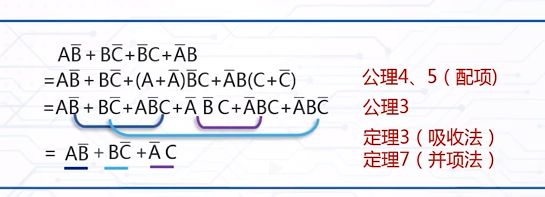
02.卡洛图化简法
什么是卡洛图？
逻辑设计中广泛使用的一种化简工具图（平面方格图 ）。其中每一个方格代表的是一个最小项。例子：两个逻辑变量的卡洛图。
三个逻辑变量的卡洛图：
四个逻辑变量的卡洛图：
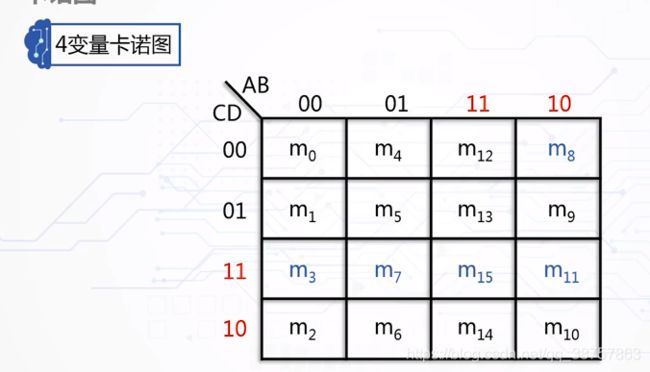
从三个开始，AB的顺序是00，01，11，10。为什么不是00，01，10，11呢？这个是因为在卡洛图中，每个相邻的项都是相邻最小项（只有一个逻辑变量不同，其他的都是相同的最小项叫做相邻最小项）。
由n个逻辑变量组成的一个最小项，会有n的相邻最小项。怎么在
卡洛图发现最小项的相邻问题呢？
01.几何上（4个逻辑变量）
如图，在m5（0101）的上下左右都是相邻最小项，分别是m1（0001），m4（0100），m13（1101），m7（0111）。这时候是几何意义上的相邻，但也是相邻最小项。
02.相关相邻
例如：m2（0010）的相邻最小项是什么？此时有几何上的m3（0011）和m6（0110），但是还缺少两个相邻的最小项。此时，把卡洛图卷起来，前后，左右卷，那么会有m0和m10出现几何意义上的相邻。
如图：
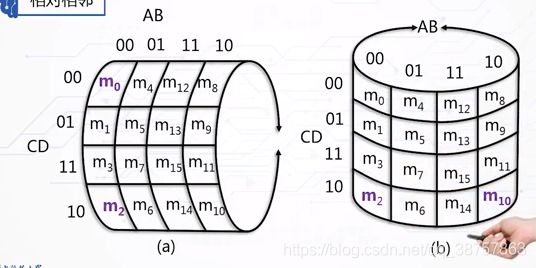
03.重叠相邻，这个出现在五个以上的逻辑变量卡洛图中。
例如：五个逻辑变量的卡洛图
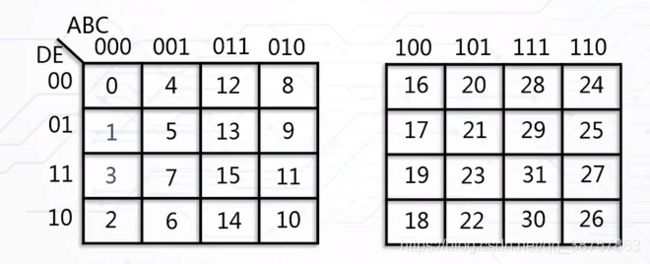
m3（00011），存在5个相邻最小项。图片几何相邻是m1（00001），m7（00111），m2（00010）。还有两个，使用左右卷，得到m11（01011），还少一个，这个时候，把两个图片进行重叠，发现m19（10011）。五个逻辑变量重叠只会出现一个相邻最小项。
逻辑函数怎么在卡洛图中进行表示？
先将一般的与-或表达式转换成标准的与-或表达式
标准的与-或表达式在卡洛图中进行表示：
01.在卡洛图中，把出现的与项，在卡洛图中标识1，其余剩下的标识0
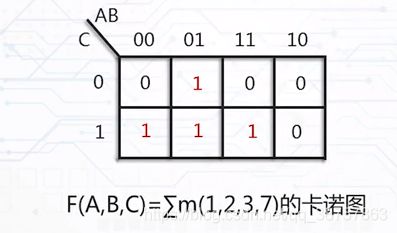
卡洛图上进行与-或表达式的化简：
化简的理由是定理7。相邻最小项的性质最重要的是两个相邻最小项是可以合并的。而卡洛图可以直观清晰的反映出相邻最小项。所以利用几何相邻，相关相邻，重叠相邻找出相邻最小项（可以化简的圈到一起，形成卡洛圈）。
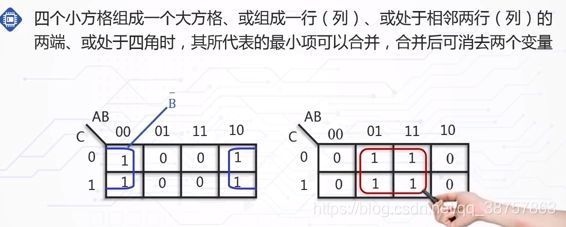
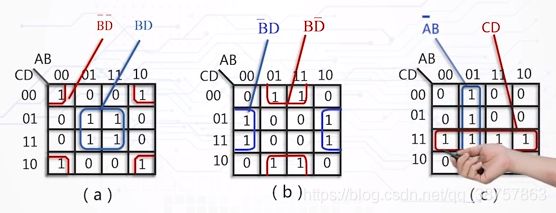
其他定义：
蕴涵项：在与-或表达式中每一个与项就是一个蕴涵式。在卡罗图中，任何一个1方格都是蕴含项。
质蕴涵项：简称为质项，所说的是与-或表达式中的这个蕴涵项，不是其他蕴含项的子集。在卡洛图中就是单个的圈1，没有被其他的大圈圈起来。
或-与表达式：
