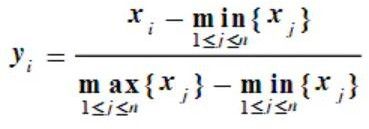基于Python实现LSTM对股票走势的预测【100010285】

摘要

为对股票价格的涨跌幅度进行预测，本文使用了基于长短期记忆网络(LSTM)的方法。根据股票涨跌幅问题， 通过对股票信息作多值量化分类，将股票预测转化成一个多维函数拟合问题。将股票的历史基本交易信息作为特征输入，利用神经网络对其训练，最后对股票的涨跌幅度做分类预测。数据集为代号 510050 的上证股票，实验结果表明该模型在单纯预测涨跌的情况下有比较好的预测效果。

一、问题描述

1.1绪论

随着我国经济的快速发展，政府、投资机构以及投资者们对股票预测的需求也越来越多。因此， 对股票价格走势的分析成为越来越多研究者关注的课题。但股票价格高度的波动性与不确定性，使其成 为计算机领域和金融领域的一大难题。

由于股票本身的波动性和不确定性，其价格是否可以被预测这一议题一直存在着不少争议。在 1956 年，Fama 提出了“有效市场假说”，指出股票的价格可以立即充分地反映市场上所有的已知信息，以及那些尚未发生但市场预期会发生的事件对股票价格的影响。这一假说为之后的股票预测工作提供了依据。

股票投资通常会选择某一类或某一只股票来作为投资对象，对这一类或一只股票进行预测，既可以将整体的股票交易信息作为训练数据，也可以只选择该类或该只股票的交易信息作为训练数据。模型有决策树、LR、支持向量机等传统机器学习的方法，也有深度学习的方法。一种最常见的股票预测方法是自回归模型，然而此类模型通常用于处理线性的稳定数据，用于处理股价存在着一定的局限性。因此也有人使用非线性模型如支持向量机、马尔可夫模型等，用以处理股票的非线性特征。

考虑到股票数据的时序性，本文选择用对时序序列有较好性能的 LSTM 网络分别对其训练，将训练好的模型用于预测次日收盘价的涨跌幅， 并对结果做对比分析。

1.2当前股票预测的方法概述

基于决策树的逐步回归算法。逐步回归算法是目前被广泛应用的一种回归算法。逐步回归算法的基本思想是：逐个引入自变量，每次引入的自变量对因变量 Y 影响最显著。每引入一个新自变量，都要对之前引入到回归方程中的旧自变量进行逐个检验，将当前方程中不显著的自 变量，从对因变量 Y 影响最小的自变量开始，进行逐个剔除，直到不能再引入新的 自变量为止。最终在回归方程中保留的自变量对因变量 Y 都是显著影响的，而不在 回归方程中的自变量对 Y 的作用都是不显著的，这样的回归方程称为最优回归方程。

SVM 方法，参考目前论文中出现频率最高的 SVM、BP 神经网 络和小波神经网络股票预测模型，分别构建了 3 个 6 输 入、1 输出的股票预测模型。输入分别为：某日上证 指数的开盘指数(价)、指数(股价)最高值、指数(股价) 最低值、收盘指数(价)、交易量和交易额；输出为输入次日的收盘指数(价)。

线性回归算法，在 CTR 预估问题的发展初期，使用最多的方法就是逻辑回归(LR)，LR 使用了 Sigmoid 变换将函数值映射到 0~1 区间，映射后的函数值就是 CTR 的预估值。LR 属于线性模型，容易并行化，可以轻松处理上亿条数据，但是学习能力十分有限，需要大量的特征工程来增加模型的学习能力。但大量的特征工程耗时耗力同时并不一定会带来效果提升。因此，如何自动发现有效的特征、特征组合，弥补人工经验不足，缩短 LR 特征实验周期，是亟需解决的问题。

深度学习算法。通过多种不同的向量表示学习方法，从不同角度抽取特征，并利用多路循环神经网络对每种特征进行单独处理，充分利用所获取的数据信息，最后再将特征进行拼接，共同对股票价格进行预测。神经网络分为多种，BP 神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，也是目前应用最广泛的神经网络；卷积神经网络(CNN)则是通过构造卷积层来提取输入特征，再利用前馈连接来完成特征的输出，它是深度学习的代表算法之一；循环神经网络(RNN)适用于输入是序列的数据，它是一种在序列的演进方向进行递归，循环单元按照链式连接的一种神经网络。

1.3本文所使用的模型

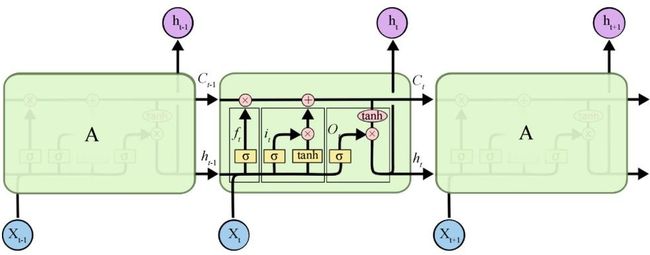
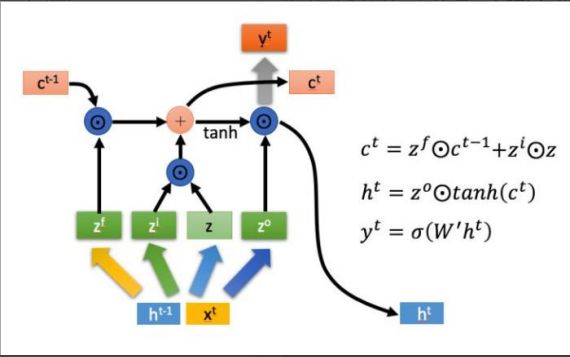
长短期记忆网络(LSTM)则是对 RNN 的一种改进，它通过引入门机制构建特殊的记忆神经单元，从而解决不能实现信息的长期依赖问题。LSTM 结构如图 1 所示，其包括输入门、输出门、遗忘门等门结构，这些门结构通过以下的递归方程来更新细胞状态，同时激活从输入到输出的映射。

图 1.3.1 LSTM 单元结构

本文主要针对预测股票涨跌幅度的目标，将其转换为一个多分类任务来进行处理。 影响股票涨跌的因素有很多，与股票本身信息相关的有其基本交易数据如开盘价、收盘价、最高价、最低价、交易量、涨跌幅等，还有交易数据衍生出的一些统计技术指标，如换手率等。 除了交易数据，股市波动还通常和舆论、政策等因素相关。但这些特征信息不能直观、即时的反映到后续的股票价格中去，同时这些信息是否与股票的基本信息耦合也尚未论证。因此本文只对股票的此类基本交易数据作为输入特征。具体细节将在第三部分阐述。

二、数据集说明

2.1tushare 库和 Talib 库概要

Tushare 是一个免费、开源的 python 财经数据接口包。主要实现对股票等金融数据从数据采集、清洗加工到数据存储的过程，能够为金融分析人员提供快速、整洁、和多样的便于分析的数据，为他们在数据获取方面极大地减轻工作量，使他们更加专注于策略和模型的研究与实现上。考虑到 Python pandas 包在金融量化分析中体现出的优势，Tushare 返回的绝大部分的数据格式都是 pandas DataFrame 类型，非常便于用 pandas/NumPy/Matplotlib进行数据分析和可视化。

TA-Lib 是一个多平台的市场分析工具，被需要对金融市场数据进行技术分析的交易软件开发人员广泛使用。它包含了 200 个指标的计算函数，如 ADX, MACD, RSI，随机指数，布林格带等。TA-Lib 为 C/ C++，Java, Perl, Python 和.NET 提供了开源的 API。TA-Lib 是在 BSD 许可下提供的，允许集成到开发者自己的开源或商业应用程序中。TA-Lib 也可以作为一个易于安装的 Excel 插件免费试用。

2.2获取历史行情数据

利用 tushare 包可以获取个股历史交易数据（包括均线数据），可以通过参数设置获取日 k 线、周 k 线、月 k 线，以及 5 分钟、15 分钟、30 分钟和 60 分钟 k 线数据。

参数说明：

• code：股票代码，即 6 位数字代码，或者指数代码（sh=上证指数 sz=深圳成指 hs300=沪深 300 指数 sz50=上证 50 zxb=中小板 cyb=创业板）
• start：开始日期，格式 YYYY-MM-DD
• end：结束日期，格式 YYYY-MM-DD
• ktype：数据类型，D=日 k 线 W=周 M=月 5=5 分钟 15=15 分钟 30=30 分

钟 60=60 分钟，默认为 D

返回值说明

• date：日期
• open：开盘价
• high：最高价
• close：收盘价
• low：最低价
• volume：成交量
• price_change：价格变动
• p_change：涨跌幅
• ma5：5 日均价
• ma10：10 日均价
• ma20:20 日均价
• v_ma5:5 日均量
• v_ma10:10 日均量
• v_ma20:20 日均量
• turnover:换手率[注：指数无此项]

在本次实验中，使用了开盘价，最高价，收盘价，最低价，成交量，价格变动，涨跌幅进行预测。

2.3实现代码：

• 设置查询股票代码，查询时间

code='510050'
date1='2000-12-01'
date2='2021-01-07'
filename='..\\data\\'
length=-1

• 调用库进行查询

df = ts.get_hist_data(code, start=date1, end=date2)
df1 = pd.DataFrame(df)

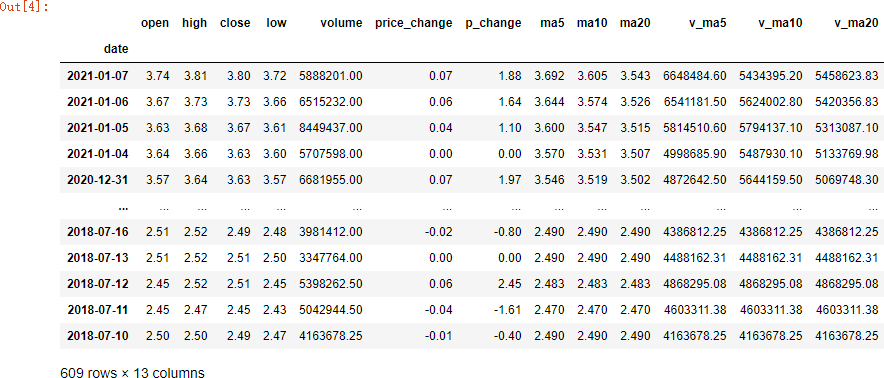
下面查看获得的数据如下：

图 2.3.1 获取历史行情数据情况

• 使用 Talib 库根据现有数据计算相应的行情指标

data['slowk'], data['slowd'] = \
talib.STOCH(df['high'].values, df['low'].values, df['close'].values,
fastk_period=9, slowk_period=3, slowk_matype=0, slowd_period=3, slowd_matyp
e=0)
data["BBANDS_upper"],data["BBANDS_middle"],data["BBANDS_lower"] =talib.BBANDS(df[
'close'].values, matype=talib.MA_Type.T3)
data["MACD"],data['MACDsignal'],data['MACDhist'] =talib.MACD(df['close'].values, fastper
iod=12, slowperiod=26, signalperiod=9)
data["ATR"] = talib.ATR(df['high'].values,df['low'].values, df['close'].values, timeperiod=14)
data["AD"] = talib.AD(df['high'].values,df['low'].values, df['close'].values, df['vol'].values)

• 最后，将得到的数据保存成 CSV 格式供进一步挖掘信息。

df1 = df1[['close','open', 'high', 'low', 'volume', 'price_change','p_change']]
df1 = df1.sort_values(by='date')
print('共有%s 天数据' % len(df1))
if length == -1:
 path = code + '.csv
 df1.to_csv(os.path.join(filename, path))
else:
 if len(df1) >= length:
 path = code + '.csv'
 df1.to_csv(os.path.join(filename, path))

2.4数据预处理

获得了以上的原生数据后，为了进行训练，还需要对原始数据进行数据预处理。为了方便训练，还是将数据分为训练集和测试集。但是需要注意的是，测试集并不是单纯用来测试，同样也可以用来训练 LSTM 模型，将数据分类的目的只是为了加速训练而已。

• 数据的归一化

在多指标评价体系中，由于个评价指标的性质，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱值水平低指标的作用，因此，为了保证结果的可靠性，需要对原始数据进行标准化处理。经验上来说，归一化就是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。

本次实验使用 Min-Max 归一化，Min-Max 标准化是指对原始数据进行线性变换，将值映射到[0，1]之间。归一化的表达式如下：

• 训练集-测试集的分割

本次实验按照时间序列，在进行中短期股票预测时将最近的百分之二的数据作为测试数据，其余的数据作为训练数据。在进行中长期股票预测时将最近的百分之十的数据作为测试数据，其余的数据作为训练数据。

2.5设计代码

stock_data = read_csv(corpusFile)
close_max = stock_data['close'].max() #收盘价的最大值
close_min = stock_data['close'].min() #收盘价的最小值
df = stock_data.apply(lambda x: (x - min(x)) / (max(x) - min(x))) 
# min-max 标准化
#根据前 n 天的数据，预测未来一天的收盘价(close)， 例如：根据 1 月 1 日、1 月 2
日、1 月 3 日、1 月 4 日、1 月 5 日的数据（每一天的数据包含 8 个特征），预测 1 月 6 日
的收盘价。
sequence = sequence_length
X = []
Y = []
for i in range(df.shape[0] - sequence):
 X.append(np.array(df.iloc[i:(i + sequence), ].values, 
dtype=np.float32))
 Y.append(np.array(df.iloc[(i + sequence), 0], 
dtype=np.float32))
# 构建 batch
total_len = len(Y)
trainx, trainy = X[:int(0.9 * total_len)], Y[:int(0.9 * total_len)]
testx, testy = X[int(0.9 * total_len):], Y[int(0.9 * total_len):]
train_loader = DataLoader(dataset=Mydataset(trainx, trainy, 
transform=transforms.ToTensor()), batch_size=batchSize,
 shuffle=True)
test_loader = DataLoader(dataset=Mydataset(testx, testy), 
batch_size=batchSize, shuffle=True)

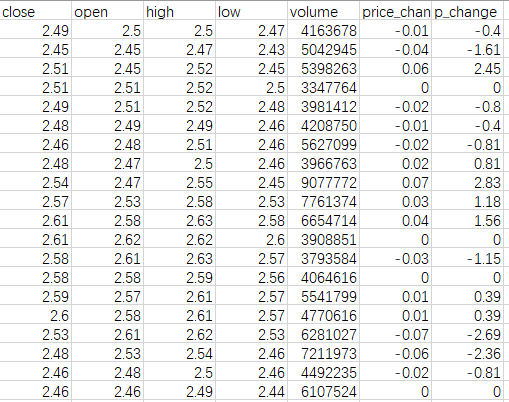
2.6股票预测使用数据说明

图 2.6.1 股票数据说明

如上图所示，本次实验主要考察 7 个指标，即：开盘价，最高价，收盘价，最低价，成交量，价格变动，涨跌幅。可以看到，对于以上的数据，量级上的差距非常大，因此需要使用 Min-Max 标准化进行预处理才能进行进一步的实验。下面对每一个特征进行分析：

• 开盘价。开盘价又称开市价，是指某种证券在证券交易所每个交易日开市后的第一笔每股买卖成交价格。世界上大多数证券交易所都采用成交额最大原则来确定开盘价。开盘价是一天起点，每一根 K 线的组成，是有开盘价、最高价、最低价和收盘价四个数据形成的在一般的情况下，开盘价没有太多的内涵，它只是昨天线的价格延续的一种反应。如果开盘价出现了非正常的现象，它就透露了一些重要的信息。
• 收盘价。收盘价指股市收盘价，为当日该证券最后一笔交易前一分钟所有交易的成交量加权平均价（含最后一笔交易）。当日无成交的，以前收盘价为当日收盘价。事实上，收盘价是市场参与者们所共同认可的价格，是一天中大家所接受的价格。而最高价是大多数人认为好的卖出价格，最低价是大多数人认为好的买进价格，而收盘价是不再进行交易的价格。因此研判收盘价有着重要意义，无论当天股价如何振荡，最终将定格在收盘价上。
• 最高价和最低价。指某种证券在每个交易日从开市到收市的交易过程中所产生的最高价格。如果当日该种证券成交价格没有发生变化，最高价就是即时价；若当日该种证券停牌，则最高价就是前收市价。最高价有时是一笔但有时会有几笔。最低价指某种证券在每个交易日从开市到收市的交易过程中所产生的最低价格。如果当日该种证券成交价格没有发生变化，最低价就是即时价；若当日该种证券停牌，则最低价就是前收市价。股票的最高价和最低价是交易当天所能达到的最高值或最低值,单从最高价和最低价是无法做出趋势判断的,最基本的方法是依据线图才有意义。
• 成交量。成交量是指在某一时段内具体的交易数。它可以在分时图中绘制，包括日线图、周线图、月线图甚至是 5 分钟、30 分钟、60 分钟图中绘制。市场成交量的变化反映了资金进出市场的情况，成交量是判断市场走势的重要指标。股票长期成交量减少，就是股票走势开始低迷的信号，如果在大盘缩量的状态下出现的话，这个信号就越强。股票上涨可以通过大的成交量或成交量逐渐放大来确认其走势；股票成交量情况是股票对大众的吸引程度真实反应，当大众看好某个股票时，股票就会有很多人买入，持有该股票的人会持股待涨，从而推动股票价格的上涨；同理，如果大众对该股票不看好，持股的人会卖出，空仓的人不会买入，从而导致股票价格的下跌。所以说成交量是股票价格的主宰。
• 价格变动。股票市场价格波动是股市运行的基础，也是股票投资者关注的焦点。股价的波动受各种经济因素和非经济因素的影响，分析这些因素的影响，可为投资者作出正确的投资决策提供一定的依据。本文结合我国股市波动的实例，从各种因素对股价影响的传导机制入手，着重对影响我国股票市场价格波动的基本因素作一般性考察。
• 涨跌幅。涨跌幅是对涨跌值的描述，用 % 表示，涨跌幅=涨跌值/昨收盘*100%。 当前交易日最新成交价（或收盘价）与前一交易日收盘价相比较所产生的数值，这个数值一般用百分比表示。在中国股市对涨跌停作出限制，因此有“涨跌停板”的说法。涨跌幅排行榜是市场热点的集中表现，根据涨跌幅排行榜.可以迅速准确地把握短时间内上涨最快风险又最小的股票，并从中判断买人和卖出的时机。根据涨跌幅排行榜既可以炒作一般短线，也可以炒作超级短线。

获得以上特征后，使用数据继续获得行情指标如下：

• 随机指标 KD：用目前股价在近阶段股价分布中的相对位置来预测可能发生的趋势反转。用法：1.D>80，超买；D<20，超卖；2.线 K 向上突破线 D，买进信号；线向下跌破线 D，卖出信号；3.线 K 与线 D 的交叉发生在 70 以上，30 以下，才有效；4.KD 指标不适于发行量小，交易不活跃的股票；5.KD 指标对大盘和热门大盘股有极高准确性。

• 布林线指标 BBANDS：1.股价上升穿越布林线上限时，回档机率大；2.股价下跌穿越布林线下限时，反弹机率大；3.布林线震动波带变窄时，表示变盘在即；4.BOLL须配合 BB 、WIDTH 使用。

• 平滑异同移动平均线 MACD：移动平滑异同平均线(Moving Average Convergence Divergence，简称 MACD 指标)策略。MACD 是查拉尔·阿佩尔(Geral Appel)于 1979年提出的，由一快及一慢指数移动平均（EMA）之间的差计算出来。“快”指短时期的 EMA，而“慢”则指长时期的 EMA，最常用的是 12 及 26 日 EMA。MACD 指标是运用快速（短期）和慢速（长期）移动平均线及其聚合与分离的征兆，加以双重平滑运算，是一种趋向类指标。根据移动平均线原理发展出来的MACD，一则去除了移动平均线频繁发出假信号的缺陷，二则保留了移动平均线的效果，因此，MACD 指标具有均线趋势性、稳重性、安定性等特点，是用来研判买卖股票的时机，预测股票价格涨跌的技术分析指标 。

• DIF 线：收盘价短期、长期指数平滑移动平均线间的差；DEA 线：DIF 线的 M 日指数平滑移动平均线；MACD 线：DIF 线与 DEA 线的差，彩色柱状线；参数：SHORT(短期)、LONG(长期)、M 天数，一般为 12、26、9。用法：1.DIF、DEA 均为正，DIFF向上突破 DEA，买入信号；2.DIF、DEA 均为负，DIFF 向下跌破 DEA，卖出信号；DEA 线与 K 线发生背离，行情反转信号；4.分析 MACD 柱状线，由红变绿(正变负)，卖出信号；由绿变红，买入信号。

• 真实波动幅度均值 ATR：今日振幅、今日最高与昨收差价、今日最低与昨收差价中的最大值，为真实波幅，求真实波幅的 N 日移动平均。参数：N 为天数，一般取 14。

• 量价指标 AD：Chaikin A/D Line 累积/派发线（Accumulation/Distribution Line），是 Marc Chaikin 提出的一种平衡交易量指标，以当日的收盘价位来估算成交流量，用于估定一段时间内该证券累积的资金流量。

  计算公式：A/D =昨日 A/D + 多空对比*今日成交量；

  多空对比= [（收盘价-最低价）-（最高价-收盘价）] /（最高价-最低价）

  若最高价等于最低价：多空对比=（收盘价/昨收盘）-1

2.7特征工程处理

• 主成分分析方法（PCA）

神经网络在大部分时候可以节省人工构建特征的时间，但它并不是万能的，仍然依赖于一个基础的特征库。此外，虽然复杂的神经网络在理论上能逼近任何连续函数，但好的特征能够有效减少模型的复杂度。

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA 的主要思想是将 n 维特征映射到 k 维上，这 k 维是全新的正交特征也被称为主成分，是在原有 n 维特征的基础上重新构造出来的 k 维特征。PCA 的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第 1,2 个轴正交的平面中方差最大的。依次类推，可以得到 n 个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面 k 个坐标轴中，后面的坐标轴所含的方差几乎为 0。于是，我们可以忽略余下的坐标轴，只保留前面 k 个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为 0 的特征维度，实现对数据特征的降维处理。

在本项目中，由于使用了开盘价、最高价、收盘价、最低价、成交量、价格变动、涨跌幅、KD、MACD 等指标，最终预测收盘价数值，各个指标相互影响，存在错综复杂的相关关系，因此使用 PCA 主成分分析方法降维是很好的特征工程方法。选取出与收盘价相关性最高的几个指标成分后，再将其输入 LSTM 神经网络训练，可以大大提高神经网络的训练效率和拟合准确度。

import numpy as np
class PCA:
def __init__(self,X):
self.X=X
def SVDdecompose(self):
B=np.linalg.svd(self.X,full_matrices=False)
self.T=B[0]*B[1]
self.P=B[2].T
lamda=B[1]
cm=[lamda[i]/lamda[i+1] for i in range(len(lamda)-1)]
return cm
def PCAdecompose(self,k):
T=self.T[:,0:k]
P=self.P[:,:k]
return T,P

图 2.7.1 主成分分析方法

2.8输出数据说明

在本次实验中，重点关注的是预测涨跌，但是在模型中将直接预测股票的涨跌数值，这个数值仅仅作为参考，实际上没有支持其合理性的依据。这么做可以提高模型包含的信息量，一定程度上能够提高准确率。

三、LSTM 模型

3.1LSTM 模型概要

长短期记忆网络（Long Short-Term Memory）是一种时间循环神经网络，是为了解决一般的循环神经网络存在的长期依赖问题而专门设计出来的，随着距离的增加，RNN 无法有效的利用历史信息。LSTM 没有这个问题。

LSTM 模型如图 1.3.1 所示，所有循环神经网络都具有神经网络的重复模块链的形式。在标准的 RNN 中，该重复模块将具有非常简单的结构，例如单个 tanh 层。LSTM 也拥有这种链状结构，但是重复模块则拥有不同的结构。与神经网络的简单的一层相比，LSTM 拥有四层，这四层以特殊的方式进行交互。

与 RTRL，BPTT，递归级联相关性相比，LSTM 在处理长期反馈更加出色,学得更快。LSTM还解决了从未有过的复杂的人工长时间延迟任务。

图 3.1.1 LSTM 内部结构模型

LSTM 内部主要有三个阶段：

• 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。具体来说是通过计算得到的z^f在来作为忘记门控，来控制上一个状态中哪些需要留哪些需要忘。
• 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 x^{t进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的z表示。而选择的门控信号则是由z}i来进行控制。将上面两步得到的结果相加，即可得到传输给下一个状态的c^t 。
• 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 来进行控制的。并且还对上一阶段得到的c^0进行了放缩。

3.2股票预测模型特征分析

• 模式识别使用特征来区分不同的种类，因此，特征提取是一个模式识别系统的关键部分。特征提取的目标是找到某种变换，将 n 维或 n×n 维的模式类别空间转换到维数更小的特征空间，并同时保留识别所需要的大部分信息。通过特征提取，模式分类可以在维数低得多的空间上进行，从而降低了计算的复杂度。而且，对给定的训练样本进行特征提取可以获得更精确的分类函数的描述，以构造更可靠的分类规则。

• 模式特征对于分类是十分重要的，股票走势的预测的关键在于能否找出有效的特征，选取的特征是否具有可辨性、可靠性、独立性和特征数量少。具体来说，特征的可辨性是指属于不同类别的样本，特征应该有相对差别较大的值，这样不同类别的样本才能区分的开；特征的可靠性是指对与属于同一类别的样本，而其应具有稳定性，这样同一类别的样本才可以判别为同一类别而不至于误判；特征的独立性是指选择出来的不同特征之间应该互不相关，这样才能减少信息的冗余性；特征的数量要少是指特征量越少越容易满足前面的三个原则，处理速度也会相应提高。

• 在本次实验中，采用的特征已经在第二节中详细阐述，具体请参见 2.6 节。

3.3本文所使用的 LSTM 结构

基于以上分析，本次实验进行如下的 LSTM 设计：

• 参数设计

  训练轮数：100 轮；

  LSTM 层数：2 层；

  输入特征的维度：7；

  隐藏层的维度：32；

  学习率：0.001；

  sequence 长度：5；即用前五天的数据来预测下一天的收盘价。

  batch size：64

• 结构设计
  LSTM 是一个 RNN 结构，并不需要分层进行设计，将上述参数引进到一个 LSTM 结构中即可。
  对于输入特征大于一个的组合，该模型的参数设置与单特征输入的涨跌预测模型略有不同。该模型的 LSTM 隐藏层展开为 30 个节点，Dense 输出层同样输出的是二维向量，并通过 softmax 函数对输出向量进行处理。采取的循环次数为 300 次，不采用小样本训练，采用 Adam 算法作为优化器，学习率为 0.0005，学习率衰减系数为 1×106，采用系数为I=0.003 的正则项。此外为稳定模型的训练，初始化权重参数为 1×108，初始化偏置参数为 0，不采用随机打散的处理方式。

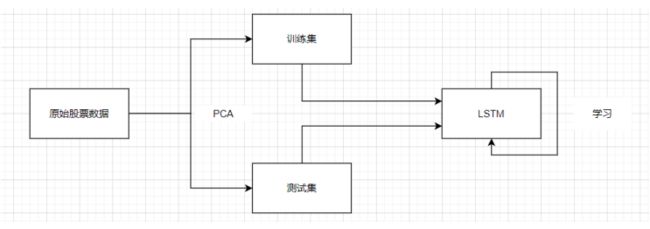
3.4本次实验所采用的结构图

图 3.4.1 实验结构图

四、实验流程和结果

4.1数据获取

使用 tushare 获得华夏上证股票的 609 条数据，获取过程见 2.5，2.6 节。

4.2Pytorch 工具集概要

PyTorch 是一个基于 Torch 的 Python 开源机器学习库，用于自然语言处理等应用程序。它主要由 Facebook 的人工智能小组开发，不仅能够 实现强大的 GPU 加速，同时还支持动态神经网络，这一点是现在很多主流框架如 TensorFlow 都不支持的。 PyTorch 提供了两个

高级功能：

• 具有强大的 GPU 加速的张量计算（如 Numpy）
• 包含自动求导系统的深度神经网络 除了 Facebook 之外，Twitter、GMU 和 Salesforce等机构都采用了 PyTorch。

4.3Pytorch 指令解析

本次实验用 Pytorch 搭建神经网络，主要使用了下列指令：class torch.nn.LSTM(*args,**kwargs)。

Pytorch 里的 LSTM 单元接受的输入都必须是 3 维的张量(Tensors).每一维代表的意思不能弄错。

第一维体现的是序列（sequence）结构,也就是序列的个数，用文章来说，就是每个句子的长度，因为是喂给网络模型，一般都设定为确定的长度，也就是我们喂给 LSTM 神经元的每个句子的长度，当然，如果是其他的带有带有序列形式的数据，则表示一个明确分割单位长度，例如是如果是股票数据内，这表示特定时间单位内，有多少条数据。这个参数也就是明确这个层中有多少个确定的单元来处理输入的数据。

第二维度体现的是 batch_size，也就是一次性喂给网络多少条句子，或者股票数据中的，一次性喂给模型多少是个时间单位的数据，具体到每个时刻，也就是一次性喂给特定时刻处理的单元的单词数或者该时刻应该喂给的股票数据的条数。

第三位体现的是输入的元素（elements of input），也就是，每个具体的单词用多少维向量来表示，或者股票数据中 每一个具体的时刻的采集多少具体的值，比如最低价，最高价，均价，5 日均价，10 均价，等等。

本实验中，使用的损失函数是 MSE，即均方损失函数，在 Pytorch 进行如下的设计：

loss_fn = torch.nn.MSELoss(reduce=True, size_average=True)

• reduce = False，返回向量形式的 loss
• reduce = True， 返回标量形式的 loss
• size_average = True，返回 loss.mean();
• 如果 size_average = False，返回 loss.sum()

默认情况下：两个参数都为 True．

本实验的梯度选择的是 adam 梯度下降方法，在 Pytorch 进行如下的设计：

optimizer = torch.optim.Adam(model.parameters(), lr=args.lr)

torch.optim 是一个实现了多种优化算法的包，大多数通用的方法都已支持，提供了丰富的接口调用，未来更多精炼的优化算法也将整合进来。 为了使用 torch.optim，需先构造一个优化器对象 Optimizer，用来保存当前的状态，并能够根据计算得到的梯度来更新参数。此处选择 adam 优化器即可。

4.4搭建 LSTM 预测模型

使用第三部分介绍的 LSTM，基于 pytorch 库，建立相应神经网络。

def __init__(self, input_size=8, hidden_size=32, num_layers=1 , output_size=1 ,
dropout=0, batch_first=True):
 super(lstm, self).__init__()
 # lstm 的输入 #batch,seq_len, input_size
 self.hidden_size = hidden_size
 self.input_size = input_size
 self.num_layers = num_layers
 self.output_size = output_size
 self.dropout = dropout
 self.batch_first = batch_first
 self.rnn=nn.LSTM(input_size=self.input_size, hidden_size=self.hidden_size,
num_layers=self.num_layers, batch_first=self.batch_first, dropout=self.dropout )
 self.linear = nn.Linear(self.hidden_size, self.output_size)

4.5拟合结果评估方法概要

本文主要通过两指标：即，accuracy 和 loss 来对拟合结果进行评估。

• accuracy：Accuracy（准确率）是机器学习中最简单的一种评价模型好坏的指标，在本次实验中，只关注预测涨跌的准确性，而对具体涨幅/跌幅不做处理。
• loss：本文的 loss 使用了均方误差进行评估，均方误差是预测的常用损失函数。

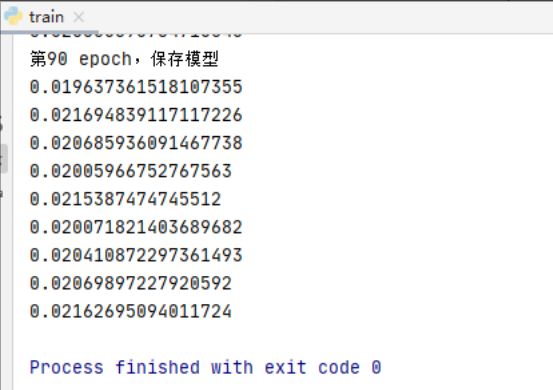
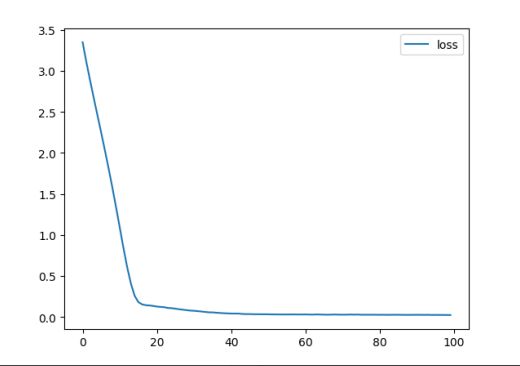
本次实验进行 100 轮神经网络训练，得到部分结果如图 4.5.1，可以看到，经过两轮训练，loss 达到了一个比较好的水平。

图 4.5.1 训练集输出结果

4.5.2 损失函数图

同时给出对训练集的预测结果和实际结果得到对比图如下，此时达到了 0.9 的准确率，可以看到，模型拟合较好，其中，纵坐标是当天收盘价相对于历史最低价的涨幅。与收盘价对应，图像的涨跌与股价涨跌一一对应。

图 4.5.2 训练集预测结果

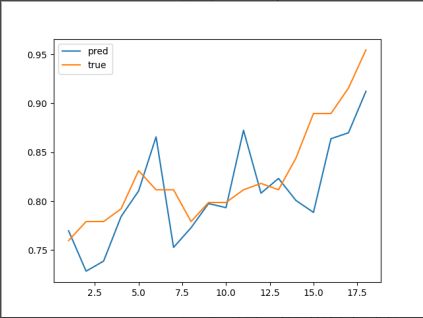
之后在给出的测试集上进行测试，对未来 14 天的走势进行预测，得到测试结果如下图，测试准确率达到了 0.55，每次价格小规模波动都会造成神经网络的较大的振动，因此在中短期预测上，神经网络表现仍然有待提高。

图 4.5.3 中短期测试数据表现

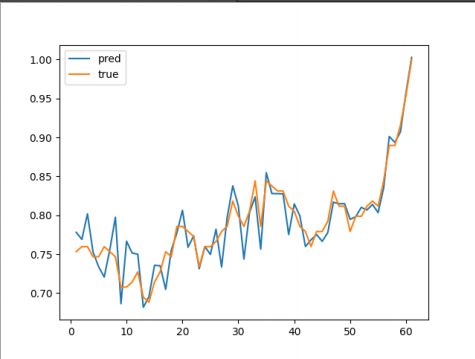
14天属于中短期预测，下面尝试进行长期预测，观察预测结果。如下图所示，对未来两个月股票走势进行预测，对涨跌的准确率达到了 0.6 对长期股市预测也有一定的参考价值。特别是最近 15 天，准确率达到了 12/15，已经非常可观。

图 4.5.4 长期测试数据表现

综合整个神经网络的性能可以看到，在中长期预测上，神经网络具有比较好的表现，原因从图 4.5.4 中可以看出，每次当实际数据变动和预测的走向相差较远时，神经网络的输出会出现较大的波动，这将导致神经网络越来越逼近现实数据，因此在长期预测上，本模型可以为决策者提供有力的参考价值。

4.6项目附件说明

本次实验项目文件有以下文件夹：stockPredict 文件夹。

• 根目录下存放使用的 python 代码。

• data 文件夹下存放获取到的股票数据。

• model 文件夹中包含已经训练好的模型。

• img 文件夹中包含测试数据表现折线图和实验结构图。

4.7项目使用说明书

本次实验项目使用方法对用户十分友好，只需要作如下操作：

• 在 parser_my 中修改需要的参数，如数据源文件，LSTM 参数等。

• train 文件用于训练。模型会自动保存。

• test 文件用于测试，结果会自动保存。

• draw 文件用于获取准确率和画出走势图，提供使用者比对。

♻️ 资源

大小： 1.63MB
➡️ 资源下载：https://download.csdn.net/download/s1t16/87354525