机器学习笔记-Logistic回归

0 - 回顾

$linearregression$如果使用平方错误的话，我们可以很方便的解析出最好的$w$是什么。即$w_{best}=X^{†}y$

1 - 逻辑斯蒂回归问题

1.1 - 问题的提出

从一个人的身体数据来判断这个人有没有心脏病，这是一个典型的二元分类问题。$\text{logistic regression}$关注的是根据一个人的身体状况来给出可能心脏病发的概率。也就是说我们想要知道的是$P(+1|x)$的值是大小。这样的问题可以称为$softbinaryclassification$，因为现在我们想要的结果不单是一个样本所属的类别是 $\times$ （是反例）或者是 $◯$（是正例）？我们关心的是取值为正例$◯$的概率的大小：如果这个值接近于$1$，那么为$◯$的可能性就大；如果这个值接近于$0$，那么为$◯$的可能性就小。

所以$\text{logistic regression}$想做的是对给定特征$x$下$y$为正例的概率$P(y=1|x)$进行建模。或者说目标函数是$f(x)=P(y=1|x)$，我们的任务是找一个最佳的模型($\text{hyperthesis}$)进行拟合。

1.2 - Soft Binary Classification

我们想要得到的目标函数是$f(x)=P(+1|x)\subseteq [0,1]$， 即针对一个输入$x$, 函数给出是正例的可能性，那么我们理想的希望拿到的数据应该是下面这样的：

$(x_1,y_1^{{}^{\prime }}=0.9=P(+1|x_1))$
$(x_2,y_2^{{}^{\prime }}=0.2=P(+1|x_2))$
$\cdots$
$(x_N,y_N^{{}^{\prime }}=0.6=P(+1|x_N))$

这样我们就可以找一个$hypothesis$ $g$， 让$g$在$data$上的表现很好(误差很小)，这样$g$可能就和我们想要的那个未知的$targetfunctionf$很相近。但是实际我们得到的数据和做$bianryclassification$时是一样的。即是下面这样的：

$(x_1,y_1^{{}^{\prime }}=1)$
$(x_2,y_2^{{}^{\prime }}=0)$
$\cdots$
$(x_N,y_N^{{}^{\prime }}=0)$

1.3 - Logistic回归的假设函数

同样的，对每一个样本$x=(x_0,x_1,x_2,\cdots ,x_d)$的所有的特征加权求和（每一个样本有$d$个维度的特征，$x_0$表示的$bias$或者是$threshold$， 相应的$w_0=1$）:

$$s=\sum _{i=0}^d{w}_i{x}_i$$

现在我们想要的并不是这个分数的大小（$\text{linear regression}$想要的是这个）。直观上我们想要分数$s$越高，对应患病风险越高；分数$s$越低，对应患病的风险越小。并且我们想要的输出是一个介于$[0,1]$之间的数(拥有概率的意义)，所以我们使用$logistic$函数（或者称为$\theta$函数）来将上述的特征加权和的$(-\infty ,+\infty )$的输出转为$[0,1]$。

所以我们要做的就是找到一个$\text{logistic hyperthesis}$来拟合$\text{target function}$。

logistic函数 $\theta$

1.4 - logistic函数:

$logistic$函数会把分数高的输出为1， 分数低的输出为0。

$$\theta (s)=\frac{e^s}{1+e^s}=\frac{1}{1+e^{-s}}$$

逻辑斯蒂回归从表面上看就是加了一个$logistic$函数的线性回归。即将线性运算的结果$w^{T}x$输入到$\theta$函数中，使用$h(x)=\frac{1}{1+exp(-w^{T}x)}$来计算在给定$x$情况下$y$为正例的概率。

2 - logistic回归的损失函数

2.1 - 三种线性的模型的对比

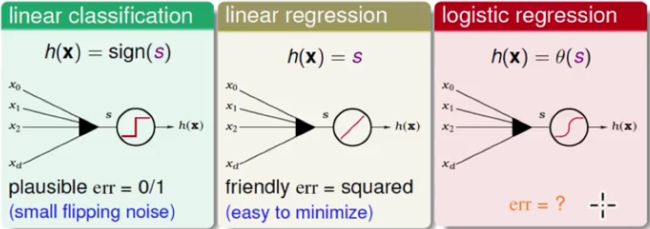
现在将$logisticregression$和我们之间接触过的$linearregression$和$linearclassification$做一些对比。三种线性的模型共同点是都计算特征的加权和：$s=w^{T}x$

在线性分类方法中，$PLA$通过关注划分错误的点也就是$er{r}_{0/1}$来进行分割线的调整；在线性回归中，我们使用平方误差$squareerror$来衡量真实值和预测值之间的差距，通过最小化平方误差可以很容易的得到线性回归的解析解；在逻辑斯蒂回归中如何去定义我们想要最小化的$E_{in}$（答案是利用似然函数）。

2.2 - 交叉熵损失/logistic损失

我们想要建模的函数表示的是样本为正例的可能性，即$h(x)=P(y=1|x)$
根据上面给出的等式可以定义：

$$P(+1|x)=h(x)，P(-1|x)=1-h(x)$$

这样，$h(x)$描述了在给定的特征$x$下该样本属于正例$(y=1)$的概率；$1-h(x)$则描述了在给定的特征$x$下该样本属于负例的概率。假设某一个数据集$D=(x_1,◯),(x_2,\times ),\cdots ,(x_N,\times )$。那么这个数据集上的似然函数为：

$$P(◯|x_1)\times P(\times |x_2)\cdots P(\times |x_N)$$

根据上面的定义可以变为：
$$h(x_1)\times (1-h(x_2))\cdots (1-h(x_N))$$

而
$$\begin{array}{rl}& 1-h(x)\\ =& 1-\frac{1}{1+e^{-w^{T}x}}\\ =& \frac{1+e^{-w^{T}x}-1}{1+e^{-w^{T}x}}\\ =& \frac{e^{-w^{T}x}}{1+e^{-w^{T}x}}\\ =& \frac{1}{1+e^{w^{T}x}}\\ =& h(-x)\end{array}$$

根据以上的性质似然函数的表达式变为：
$$\begin{array}{rl}likelihood(h)& =h(x_1)\times (1-h(x_2))\times \cdots \times (1-h(x_N))\\ & =h(x_1)\times h(-x_2)\times \cdots \times h(-x_N)\end{array}$$

那么接下来就可以利用极大似然估计法来估计模型参数。所以我们现在的目标是最大化似然函数
$$h(x_1)\times h(-x_2)\times \cdots \times h(-x_N)$$，
极大化似然函数就是令每一个样本属于其真实标记的概率极大化：
极大化$x_1$属于正例的概率$h(x_1)$ AND 极大化$x_2$属于负例的概率$h(-x_2)$（即极大化$1-h(x_2)⟶$ 极小化$h(x_2)⟶$极小化$x_2$属于正例的概率） AND$\cdots$ AND极小化$x_N$属于负例的概率。

将每一个样本的$y$写入上式可以得到似然函数：
$$likelihood(h)=\prod _{n=1}^{N}h(y_n{x}_n)$$

我们现在的目的就是 **极大化似然函数：** $$\mathop{max}\limits_{h}\prod_{n=1}^N h(y_nx_n)$$

重写一下逻辑斯蒂函数： $\theta (x)=\frac{1}{1+exp(-x)}$，
重写一下我们的逻辑斯蒂回归模型的假设函数：$h(x)=\frac{1}{1+exp(-w^{T}x)}$
那么

$$\prod _{n=1}^{N}h(y_n{x}_n)=\prod _{n=1}^N\frac{1}{1+exp(-y_n{w}^T{x}_n)}=\prod _{n=1}^N\theta (y_n{w}^T{x}_n)\text{\hspace{1em}(1)}$$

我们的目标变为寻找参数$w$使得$(1)$最大

$$ma{x}_w\prod _{n=1}^N\theta (y_n{w}^T{x}_n)$$

在机器学习中通常定义损失函数，并最小化，所以取$log$，并且变为求最小值

$$\underset{w}{\max }ln\prod _{n=1}^N\theta (y_n{w}^T{x}_n)=ma{x}_w\sum _{n=1}^{N}ln\theta (y_n{w}^T{x}_n)=mi{n}_w\sum _{n=1}^N-ln\theta (y_n{w}^T{x}_n)$$

其中

$$\theta (s)=\frac{1}{1+e^{-s}}$$

这样我们就得到了**$\text{logistic regression}$的损失函数**：
$$\begin{array}{rl}& mi{n}_w\sum _{n=1}^N-ln\theta (y_n{w}^T{x}_n)\\ & =mi{n}_w\sum _{n=1}^N-ln(\frac{1}{1+exp(-y_n{w}^T{x}_n)})\\ & =mi{n}_w\sum _{n=1}^{N}ln(1+exp(-y_n{w}^T{x}_n))\\ & =mi{n}_w\sum _{n=1}^{N}ln(1+exp(-y_n{w}^T{x}_n))\\ & =mi{n}_w\underset{E_{in}(w)}{\sum _{n=1}^{N}err(w,x_n,y_n)}\end{array}$$

这里有一个概念$err(w,x,y)=ln(1+exp(-ywx))$被定义为$crossentropyerror$。
到这里我们就把想要极大化似然函数的目的变为要极小化$E_{in}$。得到了如下的目标，下一小节讲解如何求解使得损失函数最小的$w$：
$$mi{n}_w\sum _{n=1}^{N}ln(1+exp(-y_n{w}^T{x}_n))$$

3 - Gradient of Logistic Regression Error

3.1 - 求交叉熵损失的梯度

这里给出一个结果，逻辑斯蒂的损失函数$E_{in}$也是一个凸函数。所以当我们想要最小化$E_{in}$的时候， 就是要找到该函数的“谷底”，而在“谷底”的时候梯度为0。所以最佳的$w$就是使得梯度$▽E_{in}(w)$等于$0$的$w$， 此时$E_{in}$最小。

$$E_{in}(w)=\frac{1}{N}\sum _{n=1}^{N}ln(1+exp(-y_n{w}^T{x}_n))$$

所以第一步就是求$E_{in}(w)$的梯度。

• 首先对$E_{in}(w)$求导，即计算$▽E_{in}(w)$
  $$E_{in}(w)=\frac{1}{N}\sum _{n=1}^{N}ln(\underset{\square }{1+exp(\stackrel{\circ }{-y_n{w}^T{x}_n})})$$

应用求导的链式法则对$w_i$求偏导
$$\begin{array}{rl}\frac{\partial E_{in}(w)}{\partial w_i}& =\frac{1}{N}\sum _{n=1}^N(\frac{\partial ln(\square )}{\partial \square })(\frac{\partial (1+exp(\circ ))}{\partial \circ })(\frac{\partial (-y_n{w}^T{x}_n)}{\partial (w_i)})\\ & =\frac{1}{N}\sum _{n=1}^N(\frac{1}{\square })(exp(\circ ))(-y_n{x}_{n,i})\\ & =\frac{1}{N}\sum _{n=1}^N(\frac{exp(\circ )}{1+exp(\circ )})(-y_n{x}_{n,i})\\ & =\frac{1}{N}\sum _{n=1}^N\theta (\circ )(-y_n{x}_{n,i})\end{array}$$
可以得到：

$$\frac{\partial E_{in}(w)}{\partial w}=\frac{1}{N}\sum _{n=1}^N\theta (-y_n{w}^T{x}_n)(-y_n{x}_n)$$

• 求解使得梯度为0的$w$
  $$want▽E_{in}(w)=\frac{1}{N}\sum _{n=1}^N\theta (-y_n{w}^T{x}_n)(-y_n{x}_n)=0$$

这里可以看到梯度是一个加权和，其中的权值为$\theta (-y_n{w}^T{x}_n)$。一种情况是，该梯度要为0，那么所有的权值项都要为0。即$\theta (-y_n{w}^T{x}_n)$都要为0。那么此时就要求$-y_n{w}^T{x}_n$非常小，即$y_n{w}^T{x}_n\gg 0$。所有的$y_n{w}^T{x}_n$都满足远远大于0（$w^T{x}_n$和$y_n$同号），说明该数据必须是线性可分的。所以想要得到解析解是困难的。并且不同于$linearregression$，在$linearregression$中我们要求的是一个线性的方程式，但是这里是一个非线性的方程式，所以我们不可能可以得到类似与$linearregression$的$analyticsolution$。

回顾下$PLA$算法在寻求最优的$w$时所使用的方法，不像$linearregression$可以直接得到$analyticsolution$，$PLA$是一步一步的对参数$w$进行修正： 每一次看看$w$在哪个数据点犯了错， 当发现犯了错误之后就对$w$做修正，直到不再犯错。 我们可以把以上的这个过程简化的表示如下：

$$w_{t+1}\leftarrow w_t+\underset{\eta }{1}\underset{v}{[[sign(w^T{x}_n)\ne y_n]]y_n{x}_n}$$

即如果样本$(x_n,y_n)$犯错，那么就根据该样本对方向进行更新；如果没有犯错，那么就不更新。
其中的$\eta$是步长，$v$是更新的方向。当对步长和方向做不同的规定的时候， 就可以得到不同的算法。我们把这样的算法： 一步一步的改进，每一次都决定方向，然后走一小步称为$\text{iterative optimization approach}$。

Quiz

在梯度中：$▽E_{in}(w)=\frac{1}{N}{\sum }_{n=1}^N\theta (-y_n{w}^T{x}_n)(-y_n{x}_n)$，哪一个样本点的权重值是最大的。
answer:
$y_n{w}^T{x}_n$值最小的样本点。
why：
$y_n{w}^T{x}_n$的值最小，有可能是负值，也就是说此时的$w$在这个样本点上是错的。即，犯错误的点会得到比较大的权重值。

4 - 梯度下降算法

4.1 - 为什么是负梯度方向

$\text{iterative optimization}$要做的事情就是找一个合适的方向$v$，然后决定一个步长$\eta$，通过这样的方式来不断的更新$w$。

$fort=0,1,2,\cdots$
$$w_{t+1}=w_t+\eta v$$
$untilstop,returnwasg$.
其中：$v$是方向(为方便计算规范化为长度为1的向量)，$\eta$是步长。

$\text{logistics regression}$的损失函数$E_{in}(w)$是一个凸函数， 像如下的一个山谷的形状，想象当我们把一个球放在山坡的某一个地方，也就是对应于某一个$w$，这时更新的方法就是把球慢慢的滚下去（$w$向谷底的方向移动），当球滚到谷底的时候，我们就找到了梯度为0的点，也就是最佳的$w$所在的点。所以我们现在的目标就是要把球滚下去，$v$表示滚下去的方向（长度为1的向量），$\eta$表示每一步走多远。

想要最快的到达谷底（达到$E_{in}$的最小值），那么对于任意给定的一个步长$\eta >0$，一个比较贪心的想法是我们要选择一个“最陡”的下降方向$v$来做更新（选择一个最陡的方向滚下去）。因为每一步能走的距离是一定的(一步只可以走30公分)，所以现在需要的是选择好的方向$v$：所谓好的方向就是使得沿着这个方向走了一步之后下降了最多：即使得$E_{in}(w_{w+1})$最小：

$$\underset{||v||=1}{\min }{E}_{in}(\underset{w_{t+1}}{w_t+\eta v})$$

这样的好的方向怎么决定呢？
利用泰勒（Taylor expansion：简单理解为一条曲线可以在很小的范围内被一条直线近似的替代）展开，如果$\eta$是足够小的。那么可以得到：

$$E_{in}(w_t+\eta v)\approx E_{in}(w_t)+\eta v^T▽E_{in}(w_t)$$

这样的话，原来的问题：$mi{n}_{||v||=1}{E}_{in}(w_t+\eta v)$变为如下的线性问题：

$$mi{n}_{||v||=1}\underset{known}{E_{in}(w_t)}+\underset{givenpositive}{\eta }\underset{unknown}{v^T}\underset{known}{▽E_{in}(w_t)}$$

所以现在的情况是：$E_{in}(w_t)$, $▽E_{in}(w_t)$, $\eta$都是已知的。想要知道的是什么样子的$v$可以使得该式子最小。
因为$E_{in}(w_t)$, $\eta$都是已知的， 所以我们的最小化目标可以变为下式：

$$mi{n}_{||v||=1}{v}^T▽E_{in}(w_t)$$

要使得该式子最小的最$optimal$的方向$v$就是和$▽E_{in}(w_t)$的方向相反那个向量（两个向量正好方向相反的时候內积会最小），又我们要求$v$是单位向量， 所以可以得到最好的更新权重的方向是：

$$v=-\frac{▽E_{in}(w_t)}{||▽E_{in}(w_t)||}$$

即，梯度的负方向！

4.2 - 梯度下降算法

得到了最好的方向， 我们就可以对$w$来进行更新（就知道了球应该会怎么滚）， 对于一个小的$\eta$， 权重的更新规则如下：
$$w_{t+1}=w_t-\eta \frac{▽E_{in}(w_t)}{||▽E_{in}(w_t)||}$$
即，往梯度的反方向走一小步。这个方法就是$gradientdescent$，只要能算出梯度，这个问题就可以解决。

4.3 - 如何选择步长

已经解决了更新的方向的问题， 现在我们考虑步长的问题。

对于$\eta$的设置，太小或者太大都不合适。一个不错的选择是步长最好是正比与梯度。**梯度大的时候，步长大一点；梯度小的时候，步长小一点。**也就是说比较好的步长应该是这样的$\hat{\eta }=\lambda ||▽E_{in}(w_t)||$.这样，原来的更新规则：
$$w_{t+1}=w_t-\eta \frac{▽E_{in}(w_t)}{||▽E_{in}(w_t)||}$$
得到$gradientdescent$最终的更新规则：

$$w_{t+1}=w_t-\eta ▽E_{in}(w_t)$$

4.4 - 逻辑斯蒂回归算法

现在我们得到了完整的$logisticregression$算法的流程如下：

---

初始化$w_0$
$Fort=0,1,\cdots$

1. 计算梯度
   $$▽E_{in}(w)=\frac{1}{N}\sum _{n=1}^N\theta (-y_n{w}^T{x}_n)(-y_n{x}_n)$$
2. 梯度下降更新权重
   $$w_{t+1}=w_t-\eta ▽E_{in}(w_t)$$

$\cdots$ 直到$▽E_{in}(w)\approx 0$ 或者已经更新了足够多的步数
返回最新的$w_{t+1}$作为$g$。

---

在每一个迭代步中，花费最大是计算梯度：所有的样本的$\theta$函数值和样本值的乘积和。

5 - 总结

这篇介绍了$\text{logistic regression}$，从我们想要直接计算$P(+1|x)$的值这个问题出发，我们使用$logisticfunction$作为假设函数，并且定义了$cross$-$entropyerror$。我们想要最小化这个$error$，那么就要计算这个$error$的梯度， 得到的梯度是$\theta$函数和资料的乘积的一个求和平均。但是我们没有办法直接得到梯度为$0$时候$w$的解，所以就引出了$gradientdescent$这样的$iterativeoptimizationapproach$可以帮助我们找到最佳的权重值$w$， 从而构造模型。