并查集--带权并查集

一种相对高级的、精巧实用的数据结构
三个步骤：初始化，合并，查找
两个作用：
1.将两个集合合并（合并） 近乎O（1）
2.询问两个元素是否在一个集合当中（查找） 近乎O（1）

经典应用：
连通性判断
最小生成树kruskal算法
最近公共祖先 LCA算法

初始化

用一个数组表示集合（表示多叉树），每个集合有一个编号
数组的下标为元素的id标志，数组值为其祖先
通常有两种初始化方法
第一种：每个人分别是自己的祖先 s[ i ] = i
第二种：数组s[ i ] =以 i 为祖先的家族人个数或者深度，通常设置为负数（便于寻找祖先的结束），绝对值表示树的元素个数或者树的高度

合并

不断向多叉树中插入关系，不断合并有关系的元素；
（1）纳入一个人到我们的大家庭：拿到一个人，看他是不是属于我们的大家庭（即查看他的祖先是不是我们大家庭的祖先），如果是则不进行操作，如果不是，就把他纳入到我们的家族中，把我们的祖先设置为他的祖先

（2）合并两个大家庭：首先判断两个人的祖先是不是同一个，如果是，不进行操作，如果不是就合并两个人的祖先，将其中一个祖先设置为另外一个人祖先的儿子

查找

利用递归进行查找某个编号结点的祖先，即该结点属于的集合的编号，但是递归在深度很深的时候会比较复杂，当树是立起来的时候时间复杂度为O(n),需要进行优化。优化后查询复杂度可以达到 第一种：祖先数组值存自己，其他数组元素存父亲

#include
using namespace std;
#define MAXSIZE 10000
int pare[MAXSIZE];
int Find_root(int v)    //查找 
{
	if(pare[v]==v) return v;
	return pare[v]=Find_root(pare[v]);  //路径压缩，查找过程中让每个结点的爷爷作为该结点的爸爸 
//	return Find_root(pare[v]);  不进行路径压缩，直接往上追溯到根节点 
}
void merge(int v1,int v2)    //合并 
{
	int root1=Find_root(v1);
	int root2=Find_root(v2);
	if(root1!=root2) pare[root1]=pare[root2];   //一定要判断一下是否不相等，否则会出错
} 

int main()
{
	int n=10;      //初始化 
	for(int i=1;i<=n;i++)
	{
		pare[i]=i;
	}
	return 0;
}

第二种，祖先数组值存集合元素个数，其他数组元素存父亲

#include
using namespace std;
#define MAXSIZE 10000
int parent[MAXSIZE];
/*并查集：判断元素是否在某个集合中
          合并两个集合
合并集合优化算法：1.按秩归并（矮树并到高树上，只有两棵树高度一样时新树高度才会增加） 
	 			  2.按规模归并（小树并到大树上），一般都不会用
				  3.路径压缩 简单有效，但是会改变结点间原本的关系
				  4.按规模归并和路径压缩配合使用更高效
数组下标i代表结点，数组值pare[i]代表父节点，根节点的父节点设置为负数，即集合的高度或者元素个数 
如果要考虑结点间的关系维持不变用按秩归并比较好
不用关心结点间关系，只注重整个集合用路径压缩 
	 
	 
	 */
int Find_root(int v)     //查找
{
	if(pare[v]<0) return v;
	return pare[v]=Find_root(pare[v]);  //路径压缩，查找过程中让每个结点的爷爷作为该结点的爸爸 ,返回过程中顺带修改父亲为祖先值
//	return Find_root(pare[v]);  不进行路径压缩，直接往上追溯到根节点 
}
void merge(int v1,int v2)      //合并
{
	int root1=Find_root(v1);
	int root2=Find_root(v2);
	if(pare[root1]<pare[root2]) 
	{
		pare[root1]+=pare[root2];
		pare[root2]=root1;
	}
	else 
	{
		pare[root2]+=pare[root1];
		pare[root1]=root2;
	}
} 

int main()
{
	int n=10;     // 初始化
	for(int i=1;i<=n;i++)
	{
		parent[i]=-1;
	}
	return 0;
}

例题

并查集是可以用来维护很多额外信息的

并查集只维护父节点信息

并查集维护整棵树元素个数（或者高度）

刷题链接：https://www.acwing.com/problem/content/839/
思路分析：根节点需要存储整棵树当前元素个数，并在进行集合合并的时候更新每个集合的元素个数，直接将两个集合的元素个数相加即可
AC代码：

#include
using namespace std;
int n,m,a,b,t;
const int N=100005;
int fa[N];
char c;
int find(int x)
{
    if(fa[x]<0) return x;
    return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy) 
    {
        fa[fy]+=fa[fx];  //更新这棵树的节点数量
        fa[fx]=fy;
    }
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) fa[i]=-1;     //负数绝对值就是该树上结点的个数
    for(int i=0;i<m;i++)
    {
        cin>>c;
        if(c=='C')  
		{
			cin>>a>>b;
			if(a!=b) merge(a,b);
		}
        else 
        {
            cin>>t;
            if(t==1)   //a和b是否在一个联通块
            {
                cin>>a>>b;
                if(find(a)==find(b)) cout<<"Yes\n";
                else cout<<"No\n";
            }
            else   //a所在连通块中点的数量
            {
                cin>>a;
                cout<<-fa[find(a)]<<"\n";      //find找到的是根节点，但是以该点为根节点的树包含的点的个数是存在fa[根节点]中的
            }
        }
    }
    return 0;
} 

并查集维护每个结点到根节点的高度

刷题链接：https://www.acwing.com/problem/content/242/
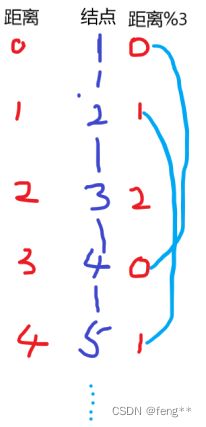
思路分析：我们将所有的结点都放在同一个集合中，并且集合中的元素间的关系都通过距离根节点的高度来决定，可以看出来这些结点间吃的关系会形成一个循环，在图中4吃3，那么4就一定是跟1是一个种类的。

1. 怎么来判断他俩是一个种类呢？
   可以发现4和1距离根节点的距离%3都是0，其他的只要是同一种类的结点离根节点的距离%3都是一样的，但是要注意一个情况，就是不能直接用dist[x]%3==dist[y]%3来断定x和y是同类的，dist[i]可能是负数的情况，假如dist[x]=-1%3=-1,dist[y]=2%3=2,按理来说x和y应该是同一类别的，但是由于负数取余导致了他俩不是一个类别，因此为了避免这种情况出现，将两个结点为一个类别表示为 (dist[x]-dist[y])%3 = 0
2. 那怎么来判断两个结点间的吃和被吃的关系呢？
   可以发现当x距离根节点的距离%3比y距离根节点的距离%3大1的时候x是吃y的（简单的就是x比y大1），也是为了避免负数存在导致答案错误，将x吃y的关系表示为 (dist[x]-dist[y])%3 = 1，也等价于 (dist[x]-dist[y]-1)%3 = 0
   
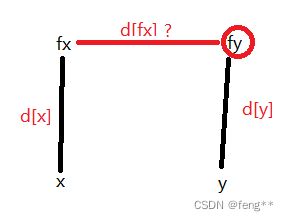
3. 怎么将不在一个集合的x和y进行合并的时候将x和y的关系设置为同类关系呢？
   看下图，我们实际是通过自主设定dist[fx]的值来将x和y的关系进行设定，因为在x和y进行合并的时刻，我们将dist[fx]的值好，使得(d[x]+d[fx]-d[y])%3=0，虽然这个时候对dist[x]和dist[y]还没有影响，还没能将(d[x]-d[y])%3=0，但是在下一次find的时候对这棵树进行压缩的时候，dist[x]就会计算为dist[x]+dist[fx]，那么这时(d[x]-d[y])%3就等于0了，达到了我们想要的效果。
4. 怎么将不在一个集合的x和y进行合并的时候将x和y的关系设置为x吃y的关系呢？
   同理，只需要设置dist[fx]的值，使得(d[x]+d[fx]-d[y]-1)%3=0即可。
   
   AC代码：

#include
using namespace std;
int n,k,d,x,y;
const int N=50005;
int fa[N],dist[N];
int find(int x)
{
	if(fa[x]!=x)
	{
		int t=find(fa[x]);    //一直往上找到根节点，并且在找的过程中将上面的结点进行压缩并求出到根节点的距离 
		 //x距离根节点的距离为dist[x]+dist[fa[x]] 
		dist[x]+=dist[fa[x]];   //递归出来后x结点之上的所有结点都进行了压缩并且dist数组都就绪了，此时求出x距离根节点的距离 
		fa[x]=t;          //最后再将x压缩为根节点的直接孩子     
	}
	return fa[x];	  //返回根节点 
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin>>n>>k;
    for(int i=1;i<=n;i++) fa[i]=i;
    int ans=0;
    while(k--)
    {
        cin>>d>>x>>y;
        if(x>n||y>n)
        {
        	ans++;continue;
        }
        if(d==1)     //x和y同类
        {
        	int fx=find(x),fy=find(y);
        	if(fx!=fy)    //不在同一个集合中，进行合并，并将二者的关系设置为x与y同类 
        	{
        		fa[fx]=fy;
        		// (d[x]+d[fx]-d[y])%3=0;  满足这个条件的为同一类别
				dist[fx]=dist[y]-dist[x]; 
        	}
        	else   //在同一个集合中，判断这两者是不是同类别 
        	{
        		//(d[x]-d[y])%3==0
        		if((dist[x]-dist[y])%3)  ans++;   //两者间的距离不是3的整数倍，就不是同一类别 
        	}
        }
        else   //x吃y 
        {
        	int fx=find(x),fy=find(y);
        	if(fx!=fy)    //不在同一个集合中，进行合并,并将二者关系设定为x吃y 
        	{
        		fa[fx]=fy;
        		// (d[x]+d[fx]-d[y])%3=1;  满足这个条件的为x吃y 
				//即 (d[x]+d[fx]-d[y]-1)%3=0
				dist[fx]=dist[y]-dist[x]+1; 
        	}
        	else   //在同一个集合中，判断这两者是不是x吃y的关系 
        	{
        		//(d[x]-d[y]-1)%3==0
        		if((dist[x]-dist[y]-1)%3)  ans++;  
        	}
        }
    }
    cout<<ans<<endl;
    return 0;
} 

即维护集合个数也维护每个结点到根节点的高度

刷题链接：https://www.acwing.com/problem/content/240/
思路分析：
根节点的父亲为该集合元素个数
另外维护每个结点到根节点的距离，
第i列所在的所有舰艇保持原来的顺序接在第j列的尾部，那么dist[i]即i到j所在集合的根节点的距离就应该等于第j列元素的个数，i的孩子们不用管了，在后面find的时候会进行距离的更新，其他的就是正常的并查集的基本操作了。
AC代码：

#include
#include
using namespace std;
const int N=30005;
int t,n,i,j;
char c;
int fa[N],d[N];
int find(int x)
{
	if(fa[x]<0) return x;
	
    int t=find(fa[x]);
    d[x]+=d[fa[x]];
    fa[x]=t;
    return fa[x];
}
int main()
{
    cin>>t;
    for(int k=1;k<=N;k++) fa[k]=-1;   //根节点的父亲存储该集合的元素个数 
    while(t--)
    {
        cin>>c>>i>>j;
        int fi=find(i),fj=find(j);
        //cout<
        if(c=='M')    //i接在j尾部,d[i]即i距离j所在集合根节点的距离为j所在集合元素个数（注意不能加一了，因为与根节点的距离从0开始计数） 
        {
        	if(fi!=fj)    //如果已经在同一个集合中了就不用再进行合并，不然会报错 
        	{
        		d[fi]=-fa[fj];  
	            fa[fj]+=fa[fi];   //将i所在集合并入j所在集合后，j集合个数要增加 
	            fa[fi]=fj;    //这块儿除了更新d，其他操作都是基本的并查集的操作，不能写fa[fi]=j 
        	}
        }
        else   //判断i和j是否处于一列
        {
            if(fi!=fj) cout<<-1<<endl;
            else if(i==j) cout<<0<<endl;    //自己和自己之间是没有其他舰艇的 
			else cout<<abs(d[j]-d[i])-1<<endl;
        }
    }
    return 0;
}

做题提醒：要并查必压缩（路径压缩为并查集的核心部分）