机器学习笔记之正则化(二)权重衰减角度(直观现象)
机器学习笔记之正则化——权重衰减角度[直观现象]
- 引言
-
- 回顾:拉格朗日乘数法角度观察正则化
-
- 过拟合的原因:模型参数的不确定性
- 正则化约束权重的取值范围
- L 1 L_1 L1正则化稀疏权重特征的过程
- 权重衰减角度观察正则化
-
- 场景构建
- 权重衰减的描述过程
- 权重衰减与过拟合之间的联系
- 总结
引言
上一节介绍了从拉格朗日乘数法角度观察正则化,本节从权重衰减的角度观察正则化。
回顾:拉格朗日乘数法角度观察正则化
过拟合的原因:模型参数的不确定性
在神经网络处理相关任务过程中,一般会对各神经元的权重 W \mathcal W W、偏置 b b b( M-P \text{M-P} M-P神经元中称为阈值 θ \theta θ)进行随机初始化操作:
Initialization Parameters : W i n i t , b i n i t \text{Initialization Parameters : }\mathcal W_{init},b_{init} Initialization Parameters : Winit,binit
在正常神经网络的训练过程中,我们并不关心 W i n i t , b i n i t \mathcal W_{init},b_{init} Winit,binit具体数值是多少。相比之下,我们更关心使得策略(损失函数)达到最小值 对应的最优解: W ∗ , b ∗ \mathcal W^*,b^* W∗,b∗。
这里无论是 W ∗ , b ∗ \mathcal W^*,b^* W∗,b∗还是 W i n i t , b i n i t \mathcal W_{init},b_{init} Winit,binit,它们均随神经网络层数的变化而描述的‘矩阵/向量’组成的集合。
以某个损失函数在权重空间中的等高线示例:
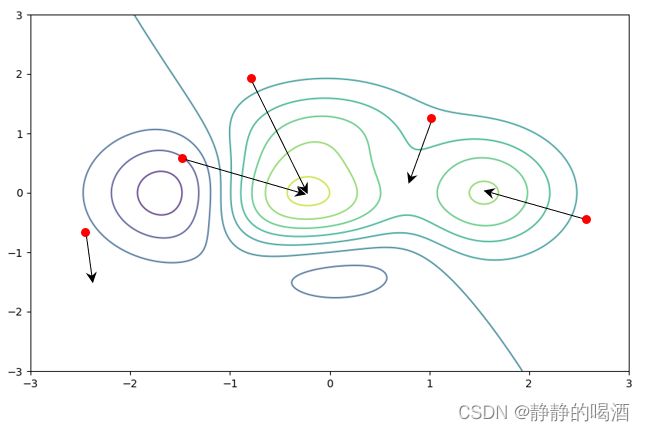
上述图像描述了某损失函数 J ( W ) \mathcal J(\mathcal W) J(W)在权重空间中的等高线。其中红色点表示在相互独立的训练过程中对应的初始化权重 W i n i t \mathcal W_{init} Winit。而黑色箭头表示使用梯度下降法 优化损失函数的过程中,权重的收敛方向。并且颜色深的部分属于高原;颜色浅的部分属于对应的低谷。
如果将中间的低谷看作是全局极小值,也就是我们期望的解。与此同时右侧的局部极小值以及两低谷之间的鞍点都有可能成为损失函数收敛的结果。由于各箭头指向的终点都会使损失函数达到最小。这使得对应的权重结果相差很大。
这说明:作为函数逼近器的神经网络,它的模型参数并不唯一,很有可能差距很大。
正则化约束权重的取值范围
通常使用 L p L_p Lp范数来约束权重的可行域范围。这里依然以 L 2 L_2 L2范数为例:
C = ∣ ∣ W ∣ ∣ 2 = ∣ w 1 ∣ 2 + ∣ w 2 ∣ 2 + ⋯ + ∣ w p ∣ 2 \mathcal C = ||\mathcal W||_2 = \sqrt{|w_1|^2 + |w_2|^2 + \cdots + |w_p|^2} C=∣∣W∣∣2=∣w1∣2+∣w2∣2+⋯+∣wp∣2
L 2 L_2 L2范数在权重空间中表示的是一个凸集合:
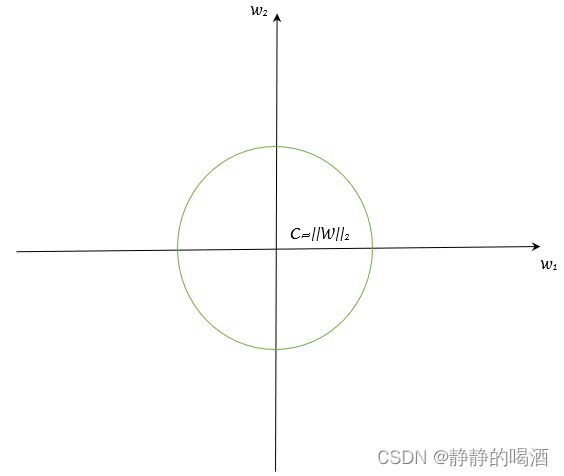
从拉格朗日乘数法的角度,观察新的目标函数 L ( W , λ ) \mathcal L(\mathcal W,\lambda) L(W,λ):
{ L ( W , λ ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 2 − C ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 − λ ⋅ C min W max λ L ( W , λ ) s . t . λ ≥ 0 \begin{cases} \begin{aligned} \mathcal L(\mathcal W,\lambda) & = \mathcal J(\mathcal W) + \lambda(||\mathcal W||_2 - \mathcal C) \\ & = \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 - \lambda \cdot \mathcal C \end{aligned} \\ \mathop{\min}\limits_{\mathcal W} \mathop{\max}\limits_{\lambda} \ \mathcal L(\mathcal W,\lambda) \\ s.t. \quad \lambda \geq 0 \end{cases} ⎩ ⎨ ⎧L(W,λ)=J(W)+λ(∣∣W∣∣2−C)=J(W)+λ∣∣W∣∣2−λ⋅CWminλmax L(W,λ)s.t.λ≥0
-
从求解最值的角度观察,由于 λ , C \lambda,\mathcal C λ,C均表示不含变量 W \mathcal W W的常数,因此并不影响最优权重 W ∗ \mathcal W^* W∗的求解结果:
W ∗ = arg W ( min W max λ J ( W ) + λ ∣ ∣ W ∣ ∣ 2 − λ ⋅ C s . t . λ ≥ 0 ) = arg W ( min W max λ J ( W ) + λ ∣ ∣ W ∣ ∣ 2 s . t . λ ≥ 0 ) \mathcal W^* = \mathop{\arg}\limits_{\mathcal W} \begin{pmatrix}\mathop{\min}\limits_{\mathcal W} \mathop{\max}\limits_{\lambda} \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 -\lambda \cdot \mathcal C \\ s.t. \quad \lambda \geq 0\end{pmatrix} = \mathop{\arg}\limits_{\mathcal W} \begin{pmatrix}\mathop{\min}\limits_{\mathcal W} \mathop{\max}\limits_{\lambda} \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 \\ s.t. \quad \lambda \geq 0\end{pmatrix} W∗=Warg(WminλmaxJ(W)+λ∣∣W∣∣2−λ⋅Cs.t.λ≥0)=Warg(WminλmaxJ(W)+λ∣∣W∣∣2s.t.λ≥0) -
如果从梯度下降角度观察,每次迭代过程需要在正则化范围内找到一个大小相等、方向相反的向量。而大小表示损失函数在正则化范围内的最优解,具体是多少我们说的不算数;但是正则化范围可以通过 λ \lambda λ人为设定。
因而可以通过调整出一个合适的 λ \lambda λ,使得该正则化范围内的最优解与迭代过程的梯度向量大小相等、方向相反即可。
相反,如果 λ \lambda λ的取值固定,同样可以通过调整 C \mathcal C C来调整正则化范围从而达到上述的效果。
L 1 L_1 L1正则化稀疏权重特征的过程
无论是调整 λ \lambda λ还是 C \mathcal C C,我们的目的都是在寻找最合适的正则化范围:
- 如果正则化范围过小,虽然出现过拟合的情况较低,但是最优解距离 J ( W ) \mathcal J(\mathcal W) J(W)中心的距离较远;模型预测的准确率是较低的;
例如下图中最小的圆形/正方形与J ( W ) \mathcal J(\mathcal W) J(W)之间的相切点。 - 相反,如果正则化范围较大,关于 J ( W ) \mathcal J(\mathcal W) J(W)影响的范围与正则化范围的重合部分会更大,因而它的预测结果会更准确;但是过大也可能导致正则化范围涵盖了 J ( W ) \mathcal J(\mathcal W) J(W)绝大部分的影响范围,那么正则化就形同虚设——不管有没有正则化,都大概率能够取到 J ( W ) \mathcal J(\mathcal W) J(W)的最优值。因而出现过拟合的可能性更高。
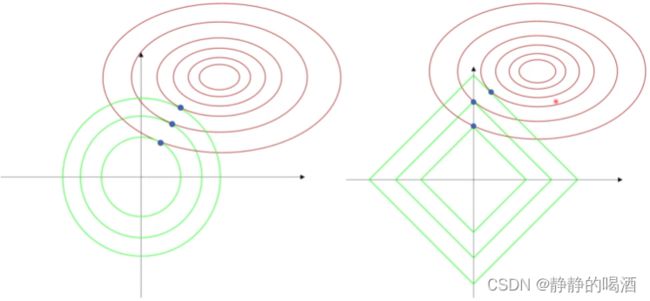
关于稀疏特征的描述,观察上图。其中左侧表示 L 2 L_2 L2正则化的图像,右侧是 L 1 L_1 L1正则化的图像。这里分别示例了 3 3 3种正则化范围的最优解。可以看出:
- L 2 L_2 L2正则化范围与 J ( W ) \mathcal J(\mathcal W) J(W)影响范围相切的位置(最优解的位置)极大可能不落在坐标轴上。不落在坐标轴上意味着该权重信息需要 w 1 , w 2 w_1,w_2 w1,w2共同作用产生的结果。
- L 1 L_1 L1正则化范围与 J ( W ) \mathcal J(\mathcal W) J(W)影响范围相切的位置(最优解的位置)相比之下有更大的概率落在坐标轴上。这意味着此时该权重信息仅和 w 2 w_2 w2相关, w 1 w_1 w1权重的分量几乎不影响权重结果。
权重衰减角度观察正则化
场景构建
对于某神经网络的权重(偏置包含在权重内) W \mathcal W W对应的损失函数以及基于梯度下降法的权重更新过程表示如下:
{ Loss Function : J ( W ) Weight Update : W ⇐ W − η ⋅ ∇ W J ( W ) \begin{cases} \text{Loss Function : }\mathcal J(\mathcal W) \\ \text{Weight Update : } \mathcal W \Leftarrow \mathcal W - \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \end{cases} {Loss Function : J(W)Weight Update : W⇐W−η⋅∇WJ(W)
将损失函数正则化之后,对应的损失函数表示为如下形式:
J ^ ( W ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 \begin{aligned} \hat {\mathcal J}(\mathcal W) & = \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 \\ \end{aligned} J^(W)=J(W)+λ∣∣W∣∣2
权重衰减的描述过程
由于上式与 J ^ ( W ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 2 − C ) \hat {\mathcal J}(\mathcal W) = \mathcal J(\mathcal W) + \lambda(||\mathcal W||_2 - \mathcal C) J^(W)=J(W)+λ(∣∣W∣∣2−C)关于权重 W \mathcal W W的最优解是等价的;并且在正则化范围内的权重点 W \mathcal W W均满足如下式子:
∣ ∣ W ∣ ∣ 2 ≤ C ||\mathcal W||_2 \leq \mathcal C ∣∣W∣∣2≤C
将 ∣ ∣ W ∣ ∣ 2 ||\mathcal W||_2 ∣∣W∣∣2展开,并将不等式两端开平方,有:
W T W ≤ C ⇔ W T W ≤ C 2 \sqrt{\mathcal W^T\mathcal W} \leq \mathcal C \Leftrightarrow \mathcal W^T\mathcal W \leq \mathcal C^2 WTW≤C⇔WTW≤C2
但无论是 C \mathcal C C还是 C 2 \mathcal C^2 C2,它描述的都是正则化范围,并且它与权重 W \mathcal W W均无关。并且平方运算在定义域大于零的情况下是一个单调递增函数,不影响 W \mathcal W W的梯度方向。因此,关于正则化后的损失函数 J ^ ( W ) \hat {\mathcal J}(\mathcal W) J^(W)可重新表示为:
为了后续的求导运算,从 λ \lambda λ内提出一个 1 2 \frac{1}{2} 21。由于 W T W − C \sqrt{\mathcal W^T\mathcal W} - \mathcal C WTW−C与 W T W − C 2 \mathcal W^T\mathcal W - \mathcal C^2 WTW−C2并不相等,因而如果想要将 ⇒ \Rightarrow ⇒化为 = = =,那么 λ \lambda λ的成分会很复杂。但并不会改变 λ \lambda λ是常数的事实。
J ^ ( W ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 ⇒ J ( W ) + λ ⋅ ( ∣ ∣ W ∣ ∣ 2 − C ) = J ( W ) + λ ⋅ ( W T W − C ⏟ 两项均开平方 ) ⇒ J ( W ) + λ ⋅ ( W T W − C 2 ) ⇒ J ( W ) + λ W T W − λ ⋅ C 2 ⏟ 与 W 无关 = J ( W ) + α 2 W T W ( λ = α 2 ) \begin{aligned} \hat {\mathcal J}(\mathcal W) & = \mathcal J(\mathcal W) + \lambda||\mathcal W||_2 \\ & \Rightarrow \mathcal J(\mathcal W) + \lambda \cdot (||\mathcal W||_2 - \mathcal C) \\ & = \mathcal J(\mathcal W) + \lambda \cdot (\underbrace{\sqrt{\mathcal W^T\mathcal W} - \mathcal C}_{两项均开平方}) \\ & \Rightarrow \mathcal J(\mathcal W) + \lambda \cdot (\mathcal W^T\mathcal W - \mathcal C^2) \\ & \Rightarrow \mathcal J(\mathcal W) + \lambda \mathcal W^T\mathcal W - \underbrace{\lambda \cdot \mathcal C^2}_{与\mathcal W无关}\\ & = \mathcal J(\mathcal W) + \frac{\alpha}{2}\mathcal W^T\mathcal W \quad (\lambda = \frac{\alpha}{2}) \end{aligned} J^(W)=J(W)+λ∣∣W∣∣2⇒J(W)+λ⋅(∣∣W∣∣2−C)=J(W)+λ⋅(两项均开平方 WTW−C)⇒J(W)+λ⋅(WTW−C2)⇒J(W)+λWTW−与W无关 λ⋅C2=J(W)+2αWTW(λ=2α)
那么基于 J ^ ( W ) = J ( W ) + α 2 W T W \hat {\mathcal J}(\mathcal W) = \mathcal J(\mathcal W) + \frac{\alpha}{2} \mathcal W^T\mathcal W J^(W)=J(W)+2αWTW,关于 W \mathcal W W权重更新过程表示如下:
这里涉及‘矩阵求导’的内容:∂ ( W T W ) ∂ W = 2 ⋅ W \begin{aligned}\frac{\partial (\mathcal W^T\mathcal W)}{\partial \mathcal W} = 2 \cdot \mathcal W\end{aligned} ∂W∂(WTW)=2⋅W该公式见《深度学习》(花书)P143 -> 7.1 参数范数惩罚
W ⇐ W − η ⋅ ∇ W J ^ ( W ) = W − η ⋅ [ ∇ W J ( W ) + α 2 ⋅ 2 ⋅ W ] = W − η ⋅ α W − η ⋅ ∇ W J ( W ) = ( 1 − η ⋅ α ) W − η ⋅ ∇ W J ( W ) \begin{aligned} \mathcal W & \Leftarrow \mathcal W - \eta \cdot \nabla_{\mathcal W} \hat {\mathcal J}(\mathcal W) \\ & = \mathcal W - \eta \cdot \left[\nabla_{\mathcal W} \mathcal J(\mathcal W) + \frac{\alpha}{2} \cdot 2 \cdot \mathcal W\right] \\ & = \mathcal W - \eta \cdot \alpha \mathcal W - \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \\ & = (1 - \eta \cdot \alpha) \mathcal W - \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \end{aligned} W⇐W−η⋅∇WJ^(W)=W−η⋅[∇WJ(W)+2α⋅2⋅W]=W−η⋅αW−η⋅∇WJ(W)=(1−η⋅α)W−η⋅∇WJ(W)
此时,我们可以对比一下执行/未执行正则化后 W \mathcal W W更新的变化:
{ W ⇐ W − η ⋅ ∇ W J ( W ) W ⇐ ( 1 − η ⋅ α ) W − η ⋅ ∇ W J ( W ) \begin{cases} \mathcal W \Leftarrow \quad\quad\mathcal W \quad\quad\text{ }- \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \\ \mathcal W \Leftarrow (1 - \eta \cdot \alpha) \mathcal W - \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \end{cases} {W⇐W −η⋅∇WJ(W)W⇐(1−η⋅α)W−η⋅∇WJ(W)
由于 η \eta η是学习率( η > 0 \eta > 0 η>0), α \alpha α是一个与 λ \lambda λ相关的常数( α > 0 \alpha > 0 α>0),因此 W ⇒ ( 1 − η ⋅ α ) W \mathcal W \Rightarrow (1 - \eta \cdot \alpha) \mathcal W W⇒(1−η⋅α)W,权重 W \mathcal W W的数值衰减了。也就是说,梯度下降法的每次迭代过程, W \mathcal W W自身就在减小。
每次 W \mathcal W W在迭代更新的过程中, W \mathcal W W自身的变更范围在逐渐缩小;
虽然 η , α \eta,\alpha η,α都是数值较小的正值,随着梯度下降的迭代, W \mathcal W W不可避免地向 0 0 0方向缩减,最终会使更新范围缩减至 0 0 0(此时 W \mathcal W W不再发生变化)。但真实情况下,更多的情况是:在 W \mathcal W W衰减至 0 0 0之前能够达到最优解,此时 W \mathcal W W就没有必要继续衰减下去,迭代过程可以终止。
而权重衰减是指:在梯度下降的迭代过程中对 W \mathcal W W实施惩罚:每一次迭代都会减小 η ⋅ α W \eta \cdot \alpha \mathcal W η⋅αW结果。
权重衰减与过拟合之间的联系
那权重衰减是如何防止过拟合的 ? ? ?需要重新回顾产生过拟合的现象:
神经网络自身是一个函数逼近器,只要隐藏层数量 ≥ 1 \geq 1 ≥1,它可以逼近任意函数(通用逼近定理)。从函数角度观察过拟合,可以理解为:由于函数将样本的噪声特征学习的过于细致,导致在训练集内对样本空间中的样本划分的过于完美。关于图像示例表示如下:
图像来源见文章尾部链接,下同,侵删。
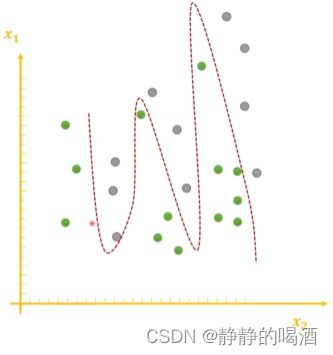
上述图像描述的是一个仅包含两个特征 x 1 , x 2 x_1,x_2 x1,x2的样本空间,并且样本空间中的点均表示训练集内的真实样本。该任务是一个二分类任务,点的颜色表示样本所属的标签分类。
由上图可知,由于样本自身存在噪声,但函数(红色虚线)对于样本划分完全正确,并且函数自身比较复杂。这样的函数对于训练集外的其他数据的泛化结果是较差的;
我们本意更希望函数对于训练集外的其他数据的泛化结果也较好。例如下面的函数:
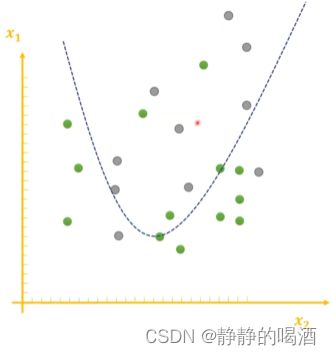
这个函数相比于上一个函数更简单,虽然存在样本没有划分正确的情况,但样本分布之间的大致趋势是正确的。那么该函数在训练集之外的其他数据中相比于过拟合的复杂函数有一个较优秀的泛化结果。
当然,函数过于简单也并不是一个好的现象,例如下面的函数:
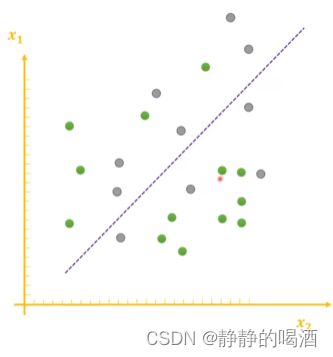
该函数也同样能够划分正确一部分样本,但它划分错误的样本同样也很多。这说明该函数并没有将样本特征学习完全,是一种欠拟合现象( Under-Fitting \text{Under-Fitting} Under-Fitting)
通过上面的三张图,我们能够看出如下规律:样本空间确定的情况下,函数越复杂,过拟合的可能性越大;函数越简单,欠拟合的可能性越大。
在使用梯度下降法对模型参数迭代的过程,本质上就是拟合函数有简单到复杂的过程。既然过拟合是大势所趋,如何在迭代过程缓和过拟合的现象呢 ? ? ?
权重衰减。
任意一个函数,我们都可以使用泰勒公式进行展开:
f ( x ) = f ( a 0 ) + 1 1 ! f ′ ( a 0 ) ( x − a 0 ) + 1 2 ! f ′ ′ ( a 0 ) ( x − a 0 ) 2 + ⋯ + 1 n ! f ( n ) ( a 0 ) ( x − a 0 ) n n ⇒ ∞ f(x) = f(a_0) + \frac{1}{1!} f'(a_0) (x - a_0) + \frac{1}{2!}f''(a_0)(x - a_0)^2 + \cdots + \frac{1}{n!}f^{(n)}(a_0)(x - a_0)^n \quad n \Rightarrow \infty f(x)=f(a0)+1!1f′(a0)(x−a0)+2!1f′′(a0)(x−a0)2+⋯+n!1f(n)(a0)(x−a0)nn⇒∞
可以观察到,上式中存在关于 x x x的一次项、平方项等等。函数的复杂程度取决于关于 x x x高次项对应的系数:
关于 1 , 1 2 , ⋯ , 1 n ! 1,\frac{1}{2},\cdots,\frac{1}{n!} 1,21,⋯,n!1它们是不会变化的常数,这里省略。
f ( a 0 ) , f ′ ( a 0 ) , f ′ ′ ( a 0 ) , ⋯ , f ( n ) ( a 0 ) n ⇒ ∞ f(a_0),f'(a_0),f''(a_0),\cdots,f^{(n)}(a_0) \quad n\Rightarrow \infty f(a0),f′(a0),f′′(a0),⋯,f(n)(a0)n⇒∞
其中 a 0 a_0 a0表示某一具体常数。如果我们想要降低函数 f ( x ) f(x) f(x)的复杂程度,我们希望:高次项的系数,也就是高阶导数数值越小越好。
我们不管函数 f ( ⋅ ) f(\cdot) f(⋅)的导数们是否复杂,不可否认的是:我们一旦将某一具体常数 a 0 a_0 a0带入这些导数中,这些导数必然是关于 W \mathcal W W的函数。这意味着:
如果W ⇒ 0 \mathcal W \Rightarrow 0 W⇒0那么f ( n ) ( a 0 ) ⇒ 0 n = 1 , 2 , ⋯ , ∞ f^{(n)}(a_0) \Rightarrow 0 \quad n=1,2,\cdots,\infty f(n)(a0)⇒0n=1,2,⋯,∞
从而 W ⇒ ( 1 − η ⋅ α ) W \mathcal W \Rightarrow (1 - \eta \cdot \alpha)\mathcal W W⇒(1−η⋅α)W,这个权重衰减过程势必也会影响 f ( n ) ( a 0 ) f^{(n)}(a_0) f(n)(a0)的减小,从而达到抑制过拟合的目的。
需要注意的是,权重衰减并不影响一次项的函数形状。因为 x x x一次项乘以一个系数,其结果必然与 x x x之间是线性相关关系。它依然是一条直线。因此,权重衰减影响的是一次以上的高次项,对一次项以及偏置项(零次项)产生的影响可以忽略不计。
总结
从整体流程观察:
- 在梯度下降迭代过程中,权重 W \mathcal W W持续衰减;
W ( t + 1 ) ⇐ ( 1 − η ⋅ α ) W ( t ) − η ⋅ ∇ W ( t ) J ( W ) \mathcal W^{(t+1)} \Leftarrow (1 - \eta \cdot \alpha)\mathcal W^{(t)} - \eta \cdot \nabla_{\mathcal W^{(t)}} \mathcal J(\mathcal W) W(t+1)⇐(1−η⋅α)W(t)−η⋅∇W(t)J(W) - W \mathcal W W的持续衰减影响函数泰勒公式展开式中 x x x各次项的系数;
其实1 1 1次项也在衰减,只不过并不影响函数形状(直线).
W ⇓ ⇒ f ( n ) ( a 0 ) ( n = 1 , 2 , ⋯ , ∞ ) ⇓ \mathcal W \Downarrow \Rightarrow f^{(n)}(a_0)(n=1,2,\cdots,\infty) \Downarrow W⇓⇒f(n)(a0)(n=1,2,⋯,∞)⇓ - 最终这些系数导致泰勒公式结果不会过于复杂,对应的函数也不会过于复杂。
相关参考:
“L1和L2正则化”直观理解(之二),为什么又叫权重衰减?到底哪里衰减了?