数据结构:树
目录
一. 树的基本概念
1.1树的定义
1.2 树的相关概念
1.3 二叉树
二、树的基本操作
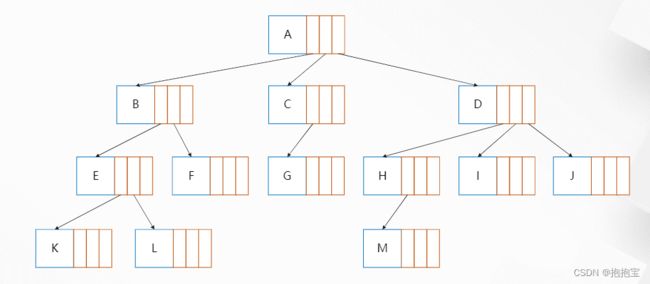
2.1 树的存储结构
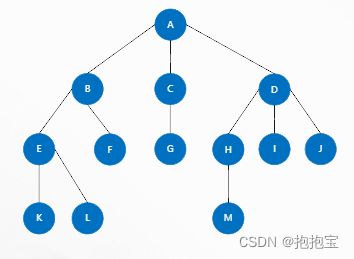
2.1.1 顺序存储结构
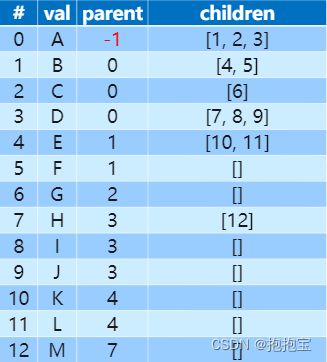
2.2.2 链式存储结构
2.2 树的增删查改
2.2.1 查找/搜索/遍历是树的核心操作
2.2.2 二叉树的深度优先搜索(DFS)
2.2.3 二叉树的广度优先搜索(BFS)
一. 树的基本概念
1.1 树的定义
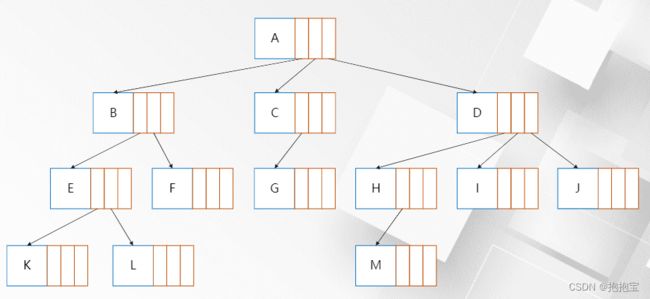
树是N(N>=0)个节点的有限集合。N=0时为空树,N>0时应满足:
有且仅有一个特定的称为根的节点
N>1时,其余节点可分为m(m>0)个互不相交的有限集合。其中,每一个有限集合自身又是一棵树
1.2 树的相关概念
1. 根节点:非空树处于最上层的唯一节点,其余节点都是它的子孙后代
2. 节点的度:节点具有的孩子节点个数
3. 叶子节点:度为0的节点
4. 父子节点:直接相连的一对节点,处于上层的是父节点,处于下层的是子节点
5. 兄弟节点:由同一个父节点生出的不同节点互称兄弟节点
6.节点层次:由根开始记为1层,其子节点为2层,孙子节点为3层……
7.节点深度:节点所在的层次数
8.树的深度/高度:树的最大层次数
9.节点高度:以节点为根的子树的深度/高度
10. 有序树:以兄弟节点为根的子树交换位置得到的新树视作与原来的树不同的树
11. 无序树:以兄弟节点为根的子树交换位置得到的新树视作与原来的树相同的树
1.3 二叉树
1.定义:二叉树是一种每个节点度都不大于2的树。其中,每个节点的子节点有左右之分且左右
子节点所在的子树不可以交换位置,即二叉树是一棵有序树。
2. 特殊的二叉树
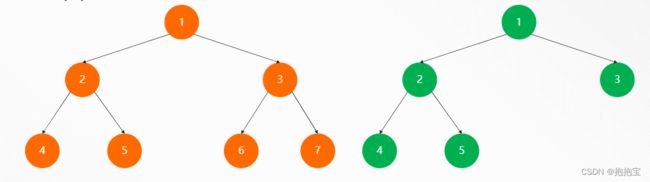
(1)满二叉树:所有叶子节点全部在最底层,且所有非叶子节点度都是2的树。
记满二叉树T的高度为h,节点总数为n,则![]() ,第k层的节点总数是
,第k层的节点总数是![]() 。
。
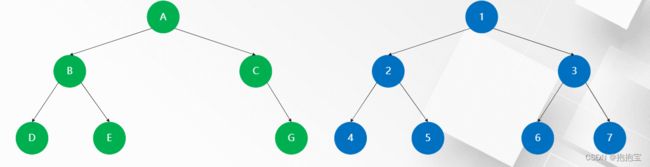
从1开始,对T从上到下,从左到右进行编号。如果编号i的节点有父节点,则其父节点的编号为i/2,如果有左字节点,则其左字节的的编号为2*i,如果有右子节点,则其右子节点的编号为2*i+1。
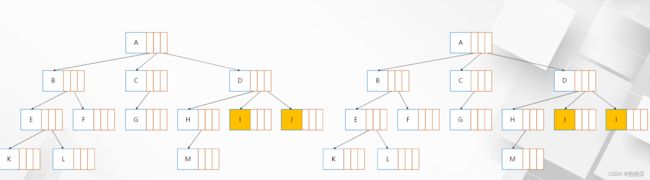
(3)完全二叉树:记二叉树高度为h。从1开始,对二叉树从上到下,从左到右进行编号。对高度
同为h的满二叉树做同样的编号处理。如果二叉树中所有节点的编号都能与满二叉树中同样位置的节点编号一致,则该二叉树是一棵完全二叉树。
- 完全二叉树的叶子节点只可能存在于最下面的两层中,且最下层的叶子节点全部是靠左紧密排列的。
- 完全二叉树中父子节点之间的编号规律与满二叉树的规律完全相同,且编号大于[n/2]的节点必是叶子节点。
- 如果n为奇数,则每个非叶子节点都有两个子节点;如果n为偶数,则第n/2个节点必为非叶子节点,且它只有左子节点而无右子节点,其余非叶子节点都有两个子节点。
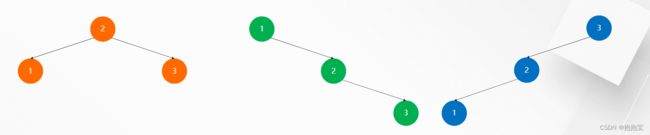
(3)二叉搜索树(BST):二叉搜索树要么是空树,要么同时满足以下条件:
1. 左子树所有节点的关键字均小于根节点的关键字
2. 右子树所有节点的关键字均大于根节点的关键字
3. 左右子树也均为二叉搜索树

(4)平衡二叉树(AVL):如果二叉树中每个节点的左右子树高度差都不大于1,则这棵二叉树就
是平衡二叉树 。
平衡二叉树经典的应用场景就是与二叉搜索树结合,形成平衡二叉搜索树。在构建二叉搜索树
的同时借助调整策略使每个节点的左右子树高度差都不大于1,保证二叉搜素树中每个节点的
左右子树都规模相当,整个树看起来更加“匀称”。
二、树的基本操作
2.1 树的存储结构
2.1.1 顺序存储结构
2.2.2 链式存储结构
2.2 树的增删查改
2.2.1 查找/搜索/遍历是树的核心操作
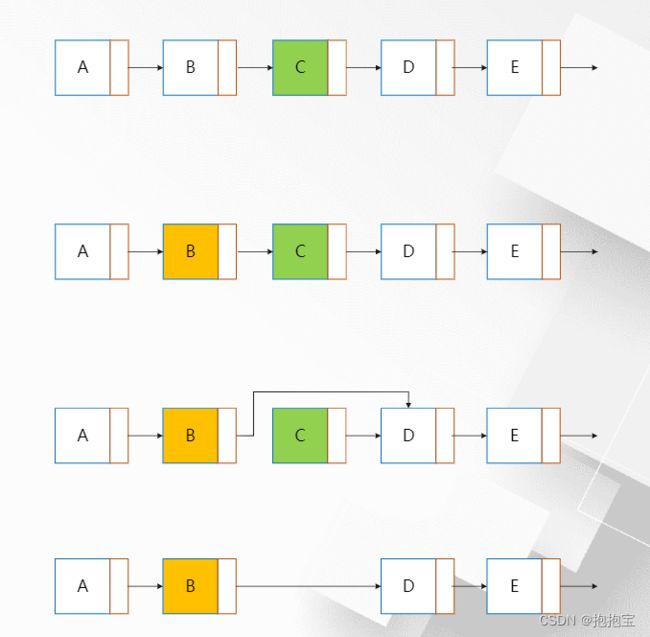
遍历:按照某种规则“访问”树中的每个节点,保证每个节点都会被“访问”到且每个节点只
会被“访问”一次
“访问”:程序与节点产生交互或者在节点进行某些操作
“进入”:程序来到了某个节点,并未与该节点产生任何交互
不同规则下,对同一个节点的“进入”次数可能有一次也可能有多次,但对同一个节点的“访
问”只会发生一次
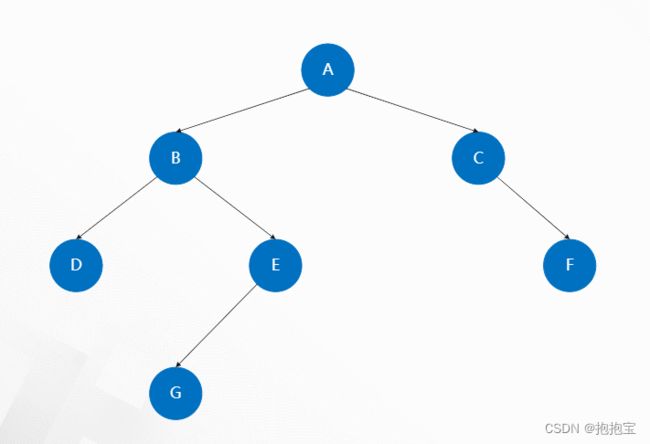
2.2.2 二叉树的深度优先搜索(DFS)
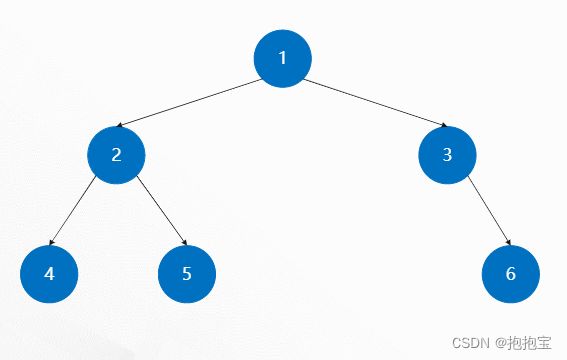
二叉树的深度优先搜索,在“进入”节点时有以下约定俗成的要求:
(1)必须以根节点为搜索起始节点并“进入”
(2)优先“进入”当前节点的左子节点,其次“进入”当前节点的右子节点
(3)如果当前节点为空节点或者左右子节点都被“进入”过,则再次“进入”父节点
根节点第一次“进入”时,其余节点均未被“进入”;第二次“进入”时,左子树节点全部完成三次“进入”;第三次“进入”时,右子树节点全部完成三次“进入”。
“进入”序列:1, 2, 4, 4, 4, 2, 5, 5, 5, 2, 1, 3, 3, 6, 6, 6, 3, 1
- 将打印操作视为一次“访问”,第一次“进入”后“访问”:1, 2, 4, 5, 3, 6;先“访问”根,再“访问”左子树,最后“访问”右子树,即先序遍历
- 将打印操作视为一次“访问”,第二次“进入”后“访问”:4, 2, 5, 1, 3, 6;先“访问”左子树,再“访问”根,最后“访问”右子树,即中序遍历
- 将打印操作视为一次“访问”,第三次“进入”后“访问”:4, 5, 2, 6, 3, 1;先“访问”左子树,再“访问”右子树,最后“访问”根,即后序遍历
2.2.3 二叉树的广度优先搜索(BFS)
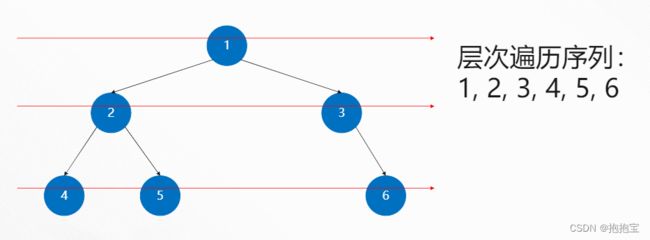
从根节点开始,按层次从上到下,同层次内从左到右“访问”每一个节点,也叫做层次遍历,每个节点只会“进入”一次。
要实现二叉树的广度优先搜索,需要借助一个特殊的数据结构——队列
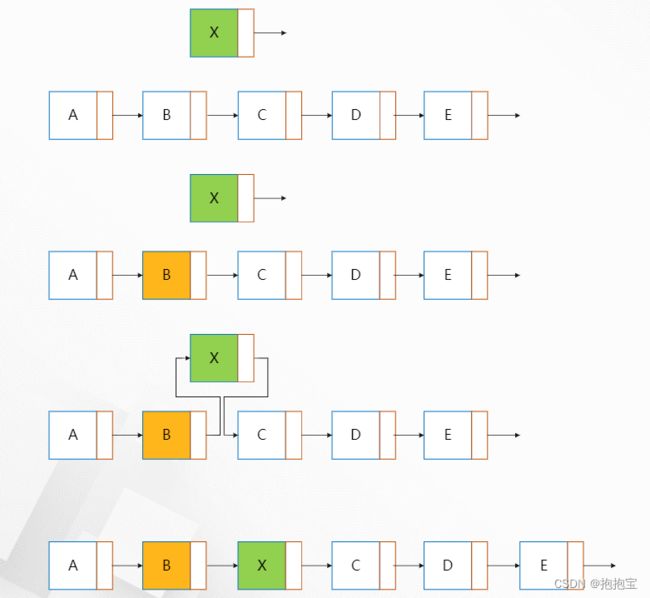
实现二叉树层次遍历的流程:
1. 初始化空队,将根节点入队
2. 当队列非空且队头元素非空时不断重复以下操作:
(1)队头节点出队并设置为当前节点
(2)对当前节点进行“访问”
(3)如果当前节点左子节点存在则将左子节点入队
(4)如果当前节点右子节点存在则将右子节点入队