数据结构 树 平衡二叉树(AVL树)
文章目录
- 平衡二叉树(AVL树)
-
- 概念
- 特点
- 相关名词
- 平衡二叉树的判断
- 操作:
-
- 插入
-
- AVL树四种插入节点的方式(调整最小不平衡子树的四种情况):
-
- LL平衡旋转(右单旋转):
- RR平衡旋转(左单旋转):
- LR平衡旋转(先左后右双旋转):
- RL平衡旋转(先右后左双旋转):
- 删除
-
- AVL树的四种删除节点方式:
-
- 删除叶子节点
- 删除的节点只有左子树
- 删除的节点只有右子树
- 删除的节点既有左子树又有右子树
- 查找
平衡二叉树(AVL树)
概念
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
特点
- 本身首先是一棵二叉搜索树。
- 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
相关名词
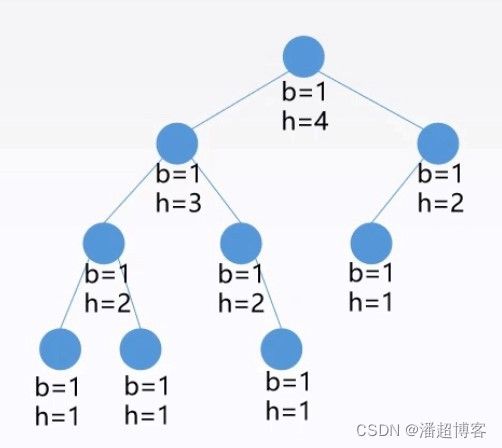
平衡因子:左子树高-右子树高;
最小不平衡子树:在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。
- 一棵不平衡的树,是有可能有多棵子树同时不平衡的。而这个时候,我们只要调整最小不平衡子树,就能够将不平衡的树调整为平衡的树。
- 平衡二叉树的不平衡调整主要是通过旋转最小不平衡子树来实现。
平衡二叉树的判断
利用递归的后序遍历过程:
- 判断左子树是一棵平衡二叉树
- 判断右子树是一棵平衡二叉树
- 判断以该结点为根的二叉树为平衡二叉树
判断条件:若左子树和右子树均为平衡二叉树,且左子树与右子树高度差的绝对值小于等于1, 则平衡。
操作:
插入
平衡二叉树插入节点步骤:
- 先插入节点;
- 然后进行调整,每次调整最小不平衡子树。
AVL树四种插入节点的方式(调整最小不平衡子树的四种情况):
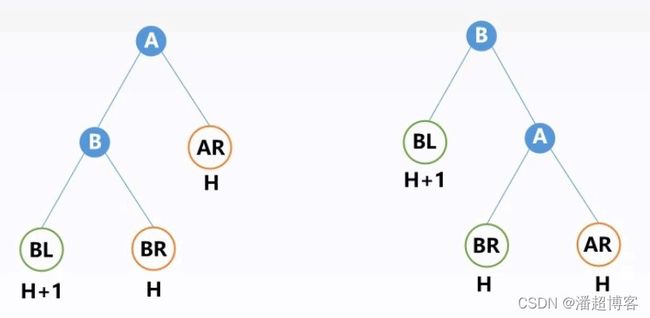
LL平衡旋转(右单旋转):
不平衡原因:在结点A的左孩子的左子树中插入新结点导致不平衡
调整方法:LL平衡旋转(右单旋转):将A的左孩子B向右上旋转代替A成为根节点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A节点的左子树。
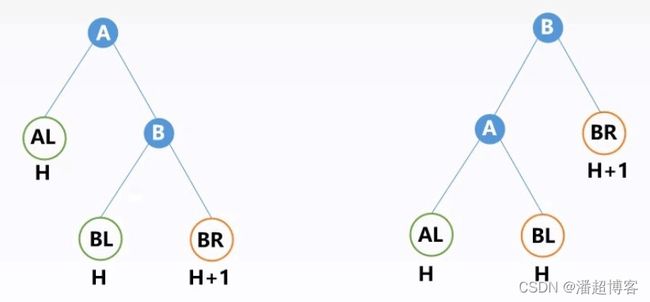
RR平衡旋转(左单旋转):
不平衡原因:在结点A的右孩子的右子树中插入新结点导致不平衡
调整方法:RR平衡旋转(左单旋转):将A的右孩子B向左上旋转代替A成为根节点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A节点的右子树。
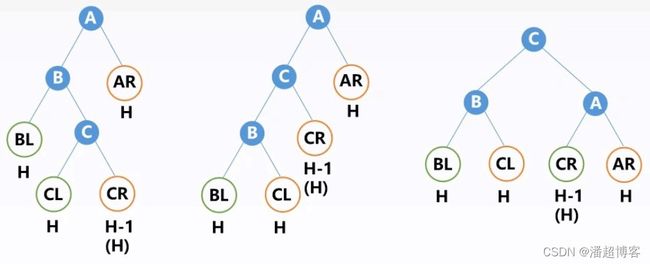
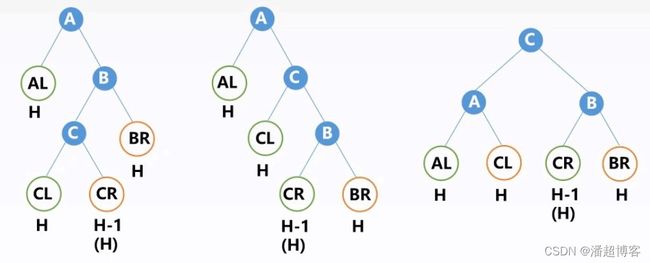
LR平衡旋转(先左后右双旋转):
不平衡原因:在结点A的左孩子的右子树中插入新结点导致不平衡
调整方法:LR平衡旋转(先左后右双旋转):先将A节点的左孩子B的右子树的根结点C向左上旋转提升到B节点的位置,然后再把该C结点向右上旋转提升到A节点的位置。
RL平衡旋转(先右后左双旋转):
不平衡原因:在结点A的右孩子的左子树中插入新结点导致不平衡
调整方法:RL平衡旋转(先右后左双旋转):先将A节点的右孩子B的左子树的根结点C向右上旋转提升到B节点的位置,然后再把该C结点向左上旋转提升到A节点的位置。
删除
从AVL树中删除可以通过把要删除的节点向下旋转成一个叶子节点,接着直接剪除这个叶子节点来完成。因为在旋转成叶子节点期间最多有 log n个节点被旋转,而每次 AVL 旋转耗费恒定的时间,删除处理在整体上耗费 O(log n) 时间。
平衡二叉树删除节点步骤:
- 完成节点的删除;
- 找到因为删除而导致不满足平衡二叉树要求的子树并对其进行调整。
对于删除操作造成的非平衡状态的修正,可以这样理解:左子树上节点的删除相当于在右子树上插入了一个新节点,右子树上节点的删除相当于在左子树上插入了一个新节点作,然后再对应上插入的四种情况选择相应的旋转就好了。
AVL树的四种删除节点方式:
- 删除叶子节点
- 删除的节点只有左子树
- 删除的节点只有右子树
- 删除的节点既有左子树又有右子树
删除叶子节点
步骤:
- 直接删除该节点;
- 检查父节点是否平衡;
- 如果平衡,一直向上检查到根节点;
- 如果全都平衡,则不需要做任何调整;
- 如果不平衡,则需要进行调整,判断失衡类型属于哪种(LL,RR,LR,RL),再进行相应的平衡化处理,然后执行步骤2检查父节点是否平衡;
调整方法:左子树上节点的删除相当于在右子树上插入了一个新节点,右子树上节点的删除相当于在左子树上插入了一个新节点,然后根据新增节点的对应方法进行调整。
例1:
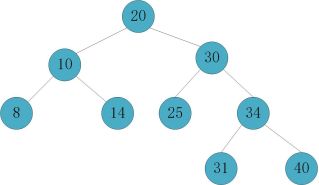
删除节点14
直接删除,检查父节点10,发现达到平衡,向上检索父节点20,发现依然达到平衡,已到达根节点,所以不需要做任何操作。
例2:
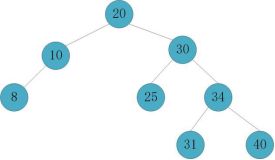
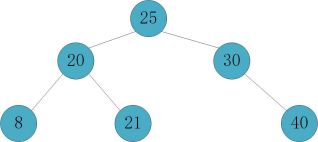
删除节点7
直接删除,检查父节点8,发现达到平衡,向上检索父节点20平衡因子为-2,20节点失衡,需要进行调整。
在左子树上删除节点其实就相当于在右子树上插入节点。
节点20的右子树根节点为30;
发现节点30的平衡因子为1,相当于在节点20的右子树节点30的左子树下插入节点,需要进行RL型调整;
先右旋(将节点30绕节点25顺时针旋转);
再左旋(将节点20绕节点25逆时针旋转);
例3:
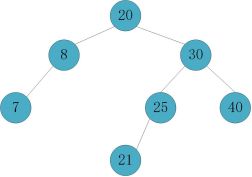
删除节点8
直接删除,检查父节点20,发现达到平衡,向上检索父节点25平衡因子为-2,25节点失衡,需要进行调整。
在左子树上删除节点其实就相当于在右子树上插入节点。
节点25的右子树根节点为30;
发现节点30的平衡因子为0,相当于在节点25的右子树节点30的右子树下插入节点,需要进行RR型调整;
进行左旋(将节点25绕节点30逆时针旋转);
删除的节点只有左子树
步骤:
- 删除节点,将其父节点与其左子树连接;
- 检查父节点是否平衡;
- 如果平衡,一直向上检查到根节点;
- 如果全都平衡,则不需要做任何调整;
- 如果不平衡,则需要进行调整,判断失衡类型属于哪种(LL,RR,LR,RL),再进行相应的平衡化处理,然后执行步骤2检查父节点是否平衡;
调整方法:左子树上节点的删除相当于在右子树上插入了一个新节点,右子树上节点的删除相当于在左子树上插入了一个新节点,然后根据新增节点的对应方法进行调整。
例1:
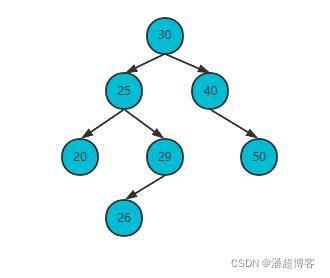
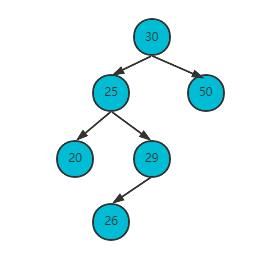
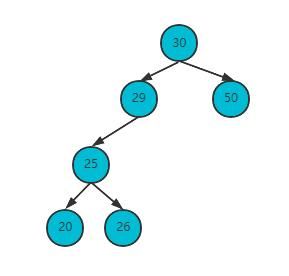
删除节点29
直接删除节点29,将父节点25和子节点26连接,发现以平衡,结束操作。
删除的节点只有右子树
步骤:
- 删除节点,将其父节点与其右子树连接;
- 检查父节点是否平衡;
- 如果平衡,一直向上检查到根节点;
- 如果全都平衡,则不需要做任何调整;
- 如果不平衡,则需要进行调整,判断失衡类型属于哪种(LL,RR,LR,RL),再进行相应的平衡化处理,然后执行步骤2检查父节点是否平衡;
调整方法:左子树上节点的删除相当于在右子树上插入了一个新节点,右子树上节点的删除相当于在左子树上插入了一个新节点,然后根据新增节点的对应方法进行调整。
例1:
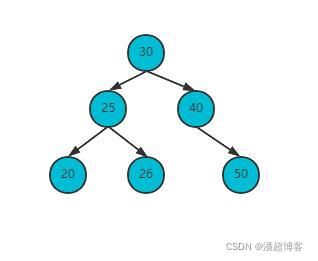
删除节点40
直接删除节点49,将父节点30和子节点50连接,发现父节点30的平衡因子为2,右子树上节点的删除相当于在左子树上插入了一个新节点,找到节点30的左孩子节点25,发现节点25的平衡因子为-1,相当于再左子树的右节点上插入节点,因此需要进行LR型调整;
先左旋;
再右旋;
删除的节点既有左子树又有右子树
步骤:
- 删除节点a;
- 判断a节点平衡因子,如果为1或者0;
- 则找到a节点左子树上最大值节点max,将max节点与a节点值进行交换,问题将会转换为删除叶子节点或删除只有左子树的节点的问题;
- 判断a节点平衡因子,如果为-1;
- 则找到a节点右子树上最小值节点min,将min节点与a节点值进行交换,问题将会转换为删除叶子节点或删除只有右子树的节点的问题;
调整方法:左子树上节点的删除相当于在右子树上插入了一个新节点,右子树上节点的删除相当于在左子树上插入了一个新节点,然后根据新增节点的对应方法进行调整。
例1:
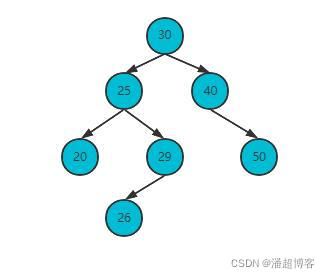
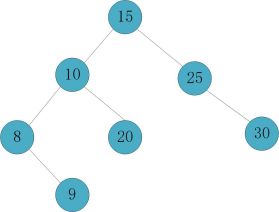
删除节点20
因为节点20平衡因子为1,将节点20和节点20左子树最大值进行交换;
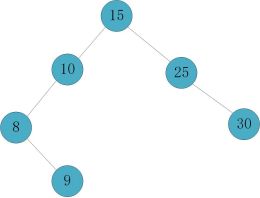
删除节点20,父节点10平衡因子变为2,失衡;
又因为节点10的左子树节点8的平衡因子为-1,相当于再节点10的左子树的右子树上进行插入节点,需要进行LR调整;
先左旋;
再右旋;
查找
在AVL树中查找同在一般BST完全一样的进行,所以耗费 O(log2n) 时间,因为AVL树总是保持平衡的。不需要特殊的准备,树的结构不会由于查询而改变。(这是与伸展树查找相对立的,它会因为查找而变更树结构。)
假设以nh表示深度为h的平衡树中含有的最少节点数;
则有n0=0,n1=1,n2=2,并且有nh=nh-1+nh-2+1;
可以证明含有n个节点的平衡二叉树的最大深度为O(log2n),平衡二叉树的平均查找长度为O(log2n)