微积分:如何理解多元函数可微和全微分?
文章目录
- 前言
- 理解一元函数微分
- 理解二元函数微分与全微分
- 总结
前言
- 在准备数学竞赛时,对多元函数微分学部分的基础概念一直存有困惑,从学数分期间至今一直没有解决,希望趁着竞赛的机会彻底弄明白这些数学概念的具体意义
- 本人非数学专业学生,下文重在理解而非严谨证明
理解一元函数微分
请注意,下文的趋近是一个过程,而不是一个状态
- 一元函数f(x)在x = a可微,即指f(x)在x = a点的切线g(x)距离实际值 f(a) 即x = a附近的实际值足够接近,以至于当x无限趋近于a时,可以用g(x)来拟合f(x)的实际值
- 同理,二元函数f(x, y)在(a, b)可微,即指f(x, y)在(a, b)点的切面g(x, y)距离实际值 f(a, b) 即(a, b)附近的实际值足够接近,以至于当(x, y)无限趋近于(a, b)时,可以用g(x, y)来拟合f(x, y)的实际值
- 当我们在证明一个函数可微时,关键是从定义出发,证明可微的本质,即对于一元函数而言,证明该点的切线与该点及其附近的实际值足够接近,以至于该切线可以拟合该点,二元函数同理
- 那么,如何衡量足够接近?
- 数学上的方式是:对于一元函数,若x无限趋近于x = a点时,x = a处的切线g(x)与实际值f(x)的差值是x变化量的高阶无穷小,则说明g(x)与f(x)足够接近,可以用切线拟合实际值,即
f ( x ) = g ( x ) + o ( Δ x ) f(x) = g(x) + o(\Delta x) f(x)=g(x)+o(Δx)
- 设g(x)的斜率为f’(a)。由于我们考察的是x = a以及该点附近的拟合情况,故 Δ x \Delta x Δx应当是在x=a附近的变化量。即在x在x = a附近变化时,|f(x)的变化量 - g(x)的变化量|应当是x的变化量的高阶无穷小
f ( x ) − f ( a ) = f ′ ( a ) Δ x + o ( Δ x ) f(x) - f(a) = f'(a)\Delta x + o(\Delta x) f(x)−f(a)=f′(a)Δx+o(Δx)
注意,此时导数是假想出来的,可微才存在导数(斜率)。此处尚未证明可微。
- 即
l i m Δ x − > 0 f ( x ) − f ( a ) Δ x lim_{\Delta x -> 0} \frac {f(x) - f(a)}{\Delta x} limΔx−>0Δxf(x)−f(a)
= f ′ ( x ) + l i m Δ x − > 0 o ( Δ x ) / Δ x = f'(x) + lim_{\Delta x -> 0} o(\Delta x)/\Delta x =f′(x)+limΔx−>0o(Δx)/Δx
- 易知,上述等式中等式右端最后一项为0与可微是充要条件。
- 通过该等式既证明了可微,又求出了导数值(极限存在,极限值)
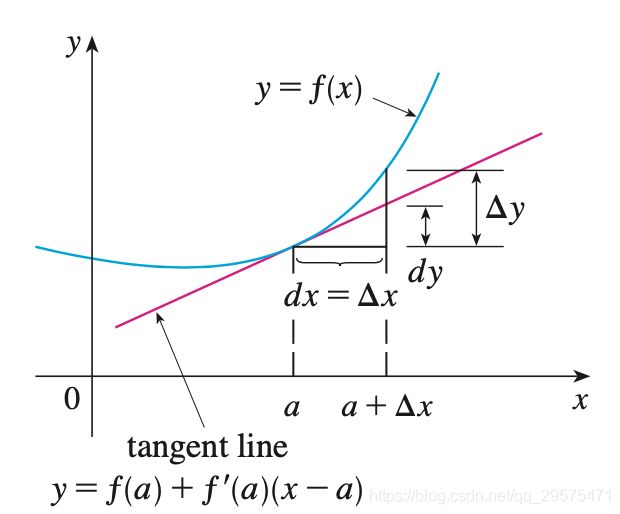
- 上图中,dx dy表示拟合值, Δ x , Δ y \Delta x, \Delta y Δx,Δy表示实际值,可微的本质就是 ∣ Δ y − d y ∣ |\Delta y - dy| ∣Δy−dy∣是 d x = Δ x dx = \Delta x dx=Δx的高阶无穷小
理解二元函数微分与全微分
- 首先,如何描述一个三维坐标轴中的平面?
- 给定一个平面中的某一点 (x0, y0, z0) ,以及该面的一个法向量 (A,B,C),则该面可以用 面上的任意一条向量和该法向量垂直 这样的数学含义来描述,即
( A , B , C ) ⋅ ( x − x 0 , y − y 0 , z − z 0 ) (A, B, C) · (x-x_0, y-y_0, z-z_0) (A,B,C)⋅(x−x0,y−y0,z−z0)
= A Δ x + B Δ y + C Δ z = 0 = A\Delta x + B\Delta y + C\Delta z = 0 =AΔx+BΔy+CΔz=0
注意这里是点乘运算,(x, y, z)是平面上的任意一点
- 根据前文描述的二元函数微分的本质,在(x0, y0)及其附近,可以用该点的切面拟合实际值,也就是需要该点及其附近的实际值与拟合值的差值是自变量变化量的高阶无穷小,即
o ( ( Δ x 2 + Δ y 2 ) 1 / 2 ) o((\Delta x^2 + \Delta y^2)^{1/2}) o((Δx2+Δy2)1/2)
- 那么,如何得到该点的切面方程呢?
- 容易证明(略),两个向量:
v 1 = ( 1 , 0 , δ z δ x ∣ x 0 , y 0 ) v1 = (1, 0, \frac {\delta z}{\delta x}|_{x0, y0}) v1=(1,0,δxδz∣x0,y0)
v 2 = ( 0 , 1 , δ z δ y ∣ x 0 , y 0 ) v2 = (0, 1, \frac {\delta z}{\delta y}|_{x0, y0}) v2=(0,1,δyδz∣x0,y0)
- 两个向量所确定的面是该点的切面
- 根据线性代数的相关技巧(略),与两个向量同时垂直的法向量应当是:
v 3 = ( δ z δ x ∣ x 0 , y 0 , δ z δ y ∣ x 0 , y 0 , − 1 ) v3 = (\frac {\delta z}{\delta x}|_{x0, y0}, \frac {\delta z}{\delta y}|_{x0, y0}, -1) v3=(δxδz∣x0,y0,δyδz∣x0,y0,−1)
- 从对一元函数可微的讨论中我们知道, Δ y \Delta y Δy是实际值的变化量,而 d y dy dy是拟合值的变化量,实际值和拟合值可以相等。切面是f(x, y)的拟合工具,故对切面的描述应该使用拟合值对应的符号,即:
v 3 ⋅ ( d x , d y , d z ) = 0 v3 · (dx, dy, dz) = 0 v3⋅(dx,dy,dz)=0
δ z δ x d x + δ z δ y d y − d z = 0 \frac {\delta z}{\delta x}dx + \frac {\delta z}{\delta y}dy - dz = 0 δxδzdx+δyδzdy−dz=0
δ z δ x d x + δ z δ y d y = d z \frac {\delta z}{\delta x}dx + \frac {\delta z}{\delta y}dy = dz δxδzdx+δyδzdy=dz
- 其中,若认为z是曲面上在该点附近的实际值,z’是在切面上该点附近的拟合值,则 Δ z = z − z 0 , d z = z ′ − z 0 \Delta z = z-z_0, dz = z' - z_0 Δz=z−z0,dz=z′−z0。
- 除此之外,易知, d x = Δ x , d y = Δ y dx = \Delta x, dy = \Delta y dx=Δx,dy=Δy
- 很好,现在我们已经得到切面方程了,这个方程和全微分方程一模一样,但它不一定就是全微分方程。如果它不满足我们上述描述的可微的实质,那么它就不是全微分方程,即全微分方程不存在,该二元函数不可微,则该切面方程只是一个长得和全微分方程一模一样的切面方程而已。
- 那么f(x, y)是否可微呢?我们需要证明最重要的一点:
Δ z − d z = o ( ( Δ x 2 + Δ y 2 ) 1 / 2 ) \Delta z - dz = o((\Delta x^2 + \Delta y^2)^{1/2}) Δz−dz=o((Δx2+Δy2)1/2)
这里不再继续写极限描述了,证明高阶无穷小即可
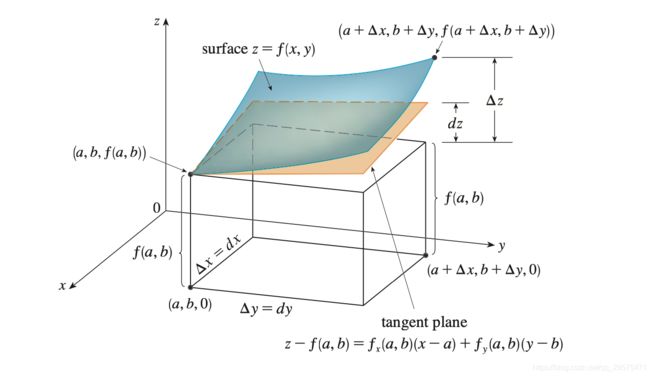
Δ z = δ z δ x Δ x + δ z δ y Δ y + o ( ( Δ x 2 + Δ y 2 ) 1 / 2 ) \Delta z = \frac {\delta z}{\delta x}\Delta x + \frac {\delta z}{\delta y}\Delta y + o((\Delta x^2 + \Delta y^2)^{1/2}) Δz=δxδzΔx+δyδzΔy+o((Δx2+Δy2)1/2)
总结
- 可微的实质很重要,竞赛中会遇到一些证明二元函数可微的题目。关键是要正确理解证明可微就是证明差值是自变量变化量的高阶无穷小
- 下一篇文章将继续解析如何理解方向导数与梯度?