用于模拟原子相互作用的continuous-filter卷积NeurIPS2017
深度学习有可能彻底改变量子化学,因为它非常适合学习结构化数据的表示。虽然卷积神经网络已被证明是图像、音频和视频数据的首选,但分子中的原子并不局限于网格结构(grid)。相反,它们的精确位置包含了基本的物理信息,如果离散化,这些信息就会丢失。因此,作者提出使用连续滤波器卷积层来建模局部相关性(local correlations),而不需要数据位于离散的grid上。作者将这些层应用于SchNet:一种新的深度学习架构,用于模拟分子中的原子相互作用。
来自:SchNet: A continuous-filter convolutional neural network for modeling quantum interactions
目录
- 背景概述
- 连续-滤波卷积
- SchNet
-
- 架构
- 基于能量和力的训练
- 实验
- 小结
背景概述
探索分子性质是一个重要问题,然而现有方法只适用于平衡的稳定系统,即势能表面 E ( r ⃗ 1 , . . . , r ⃗ n ) E(\vec{r}_{1},...,\vec{r}_{n}) E(r1,...,rn)局部极小,其中, r ⃗ i \vec{r}_{i} ri是原子 i i i的位置。现有数据集比如QM9只包含平衡的分子。
一般来说,如果不优化原子位置,如何获得平衡的构象是不清楚的。因此,我们需要计算总能量 E ( r ⃗ 1 , . . . , r ⃗ n ) E(\vec{r}_{1},...,\vec{r}_{n}) E(r1,...,rn)和作用在原子上的力: F ⃗ i ( r ⃗ 1 , . . . , r ⃗ n ) = − ∂ E ∂ r ⃗ i ( r ⃗ 1 , . . . , r ⃗ n ) \vec{F}_{i}(\vec{r}_{1},...,\vec{r}_{n})=-\frac{\partial E}{\partial\vec{r}_{i}}(\vec{r}_{1},...,\vec{r}_{n}) Fi(r1,...,rn)=−∂ri∂E(r1,...,rn)一种可能是使用计算成本更低,但也不太准确的量子化学近似。相反,作者选择将机器学习模型扩展到成分(化学)和构型(结构)自由度。
作者的目标是学习使用平衡和非平衡构象的分子表示。原子系统的这种一般表示应该遵循基本的量子力学原理。比如预测的力场必须是无旋的。否则,就有可能使得能量不断增加,即打破能量守恒定律。此外,势能曲面及其偏导数必须是光滑的。除此之外,模型还要考虑分子能量对旋转等。同时模拟化学和构象变化是机器学习模型驱动量子化学探索的重要一步。
连续-滤波卷积
在深度学习中,卷积层对图像像素、视频帧或数字音频数据等离散信号进行操作。虽然在这些情况下,在相同的grid上定义滤波器就足够了,但对于不均匀间隔的输入,例如分子的原子位置,这是不可能的,见图1。通常这可以用插值来解决,然而,选择合适的插值方案本身就是一个挑战,并且可能需要高分辨率的grid。因此,在欧氏空间之外也存在卷积的各种扩展,例如graph。类似地,作者提出使用连续滤波器,它能够处理间隔不均匀的数据,特别是任意位置的原子。
- 离散滤波器(左图)无法捕捉原子的微妙位置变化,从而导致不连续的能量预测 E ^ \widehat{E} E 。连续滤波器可以捕捉这些变化并产生平滑的能量预测。
给定一个特征表示 X l = ( x ⃗ 1 l , . . . , x ⃗ n l ) X^{l}=(\vec{x}_{1}^{l},...,\vec{x}_{n}^{l}) Xl=(x1l,...,xnl),其中 x ⃗ i l ∈ R F \vec{x}_{i}^{l}\in R^{F} xil∈RF对应一个位置 r ⃗ i ∈ R D \vec{r}_{i}\in R^{D} ri∈RD,连续滤波器卷积层 l l l需要一个滤波器生成函数: W l : R D → R F W^{l}:R^{D}\rightarrow R^{F} Wl:RD→RF它将位置映射到一个对应的滤波值。这个滤波器生成函数由神经网络建模。在位置 r ⃗ i \vec{r}_{i} ri的卷积输出 x ⃗ i l + 1 \vec{x}_{i}^{l+1} xil+1为: x ⃗ i l + 1 = ( X l × W l ) i = ∑ j x ⃗ j l ∘ W l ( r ⃗ i − r ⃗ j ) \vec{x}_{i}^{l+1}=(X^{l}\times W^{l})_{i}=\sum_{j}\vec{x}_{j}^{l}\circ W^{l}(\vec{r}_{i}-\vec{r}_{j}) xil+1=(Xl×Wl)i=j∑xjl∘Wl(ri−rj)其中, ∘ \circ ∘代表element-wise乘积。
SchNet
SchNet被设计用来学习预测分子能量和原子力的表示。它反映了基本的物理定律,包括原子indexing和平移的不变性(invariance to atom indexing and translation),原子位置的平滑能量预测以及预测力场的能量守恒。能量和力的预测分别是旋转不变和等变的。
架构
- 图2:SchNet的架构概述(左),相互作用模块(中)和带有滤波器生成网络的连续滤波卷积(右)。shifted softplus定义为 s s p ( x ) = I n ( 0.5 e x + 0.5 ) ssp(x)=In(0.5e^{x}+0.5) ssp(x)=In(0.5ex+0.5)。
图2显示了SchNet的概述。在每一层,分子以原子方式表示,类似于图像中的像素。原子之间的相互作用由三个相互作用模块来模拟。最终的预测是在原子更新特征表示和pooling所产生的原子能量之后获得的。下面将讨论网络的不同组成部分。
分子表征:具有某种构象的分子可以用 n n n个原子描述,包含原子属性 Z = ( Z 1 , . . . , Z n ) Z=(Z_{1},...,Z_{n}) Z=(Z1,...,Zn)和原子位置 R = ( r ⃗ 1 , . . . , r ⃗ n ) R=(\vec{r}_{1},...,\vec{r}_{n}) R=(r1,...,rn)。通过神经网络,使用特征表示原子 X l = ( x ⃗ 1 l , . . . , x ⃗ n l ) X^{l}=(\vec{x}_{1}^{l},...,\vec{x}_{n}^{l}) Xl=(x1l,...,xnl), x ⃗ i l ∈ R F \vec{x}_{i}^{l}\in R^{F} xil∈RF通道数为 F F F。使用依赖于原子类型 Z i Z_{i} Zi的嵌入来初始化原子 i i i的表示: x ⃗ i 0 = a ⃗ Z i \vec{x}_{i}^{0}=\vec{a}_{Z_{i}} xi0=aZi在训练过程中对原子类型嵌入 a ⃗ Z \vec{a}_{Z} aZ进行随机初始化和优化。
Atom-wise层:在SchNet中,反复出现了atom-wise层,这些是dense层,分别应用于原子 i i i的表示 x ⃗ i l \vec{x}_{i}^{l} xil: x ⃗ i l + 1 = W l x ⃗ i l + b ⃗ l \vec{x}_{i}^{l+1}=W^{l}\vec{x}^{l}_{i}+\vec{b}^{l} xil+1=Wlxil+bl这些层负责feature的重组。由于原子之间共享权重,因此该结构可以根据分子的大小(原子数量)进行扩展。
Interaction block:如图2(中)所示,Interaction块负责根据分子几何结构 R = ( r ⃗ 1 , . . . , r ⃗ n ) R=(\vec{r}_{1},...,\vec{r}_{n}) R=(r1,...,rn)更新原子表示。在整个网络的Interaction部分,将特征维数保持在 F = 64 F = 64 F=64。受到ResNet启发,interaction block采用残差连接: x ⃗ i l + 1 = x ⃗ i l + v ⃗ i l \vec{x}_{i}^{l+1}=\vec{x}_{i}^{l}+\vec{v}_{i}^{l} xil+1=xil+vil如图2所示, v ⃗ i l \vec{v}_{i}^{l} vil通过atom-wise层输出,后接一个原子间连续滤波器卷积(cfconv),然后是两个atom-wise层(中间包含softplus提供非线性变换)。
滤波器生成网络:cfconv层包括滤波器生成网络,如图2的右面板所示。为了满足分子能量建模的要求,作者将cfconv层的滤波器限制为旋转不变。旋转不变性是利用原子间距离得到的: d i j = ∣ ∣ r ⃗ i − r ⃗ j ∣ ∣ d_{ij}=||\vec{r}_{i}-\vec{r}_{j}|| dij=∣∣ri−rj∣∣作为滤波网络的输入,如果没有进一步的处理,滤波器将会高度相关,因为初始化后的神经网络接近线性。这导致在训练开始时出现一个难以克服的平缓期。作者通过用径向基函数扩展距离来避免这种情况: e k ( r ⃗ i − r ⃗ j ) = e x p ( − γ ∣ ∣ d i j − μ k ∣ ∣ 2 ) e_{k}(\vec{r}_{i}-\vec{r}_{j})=exp(-\gamma||d_{ij}-\mu_{k}||^{2}) ek(ri−rj)=exp(−γ∣∣dij−μk∣∣2)中心 0 A ˚ ≤ μ k ≤ 30 A ˚ 0Å ≤\mu_{k}≤ 30Å 0A˚≤μk≤30A˚,每 0.1 A ˚ 0.1Å 0.1A˚对应 γ = 10 A ˚ \gamma=10Å γ=10A˚,该选择使所有出现在数据集中的距离都被滤波器覆盖。基于这种额外的非线性,初始滤波器的相关性较小,从而可以更快训练。选择更少的中心 μ k \mu_{k} μk对应于降低滤波器的分辨率,而限制中心的范围对应于通常卷积层中的滤波器大小。用softplus激活将扩展的距离输入两个dense层,以计算滤波器权值 W ( r ⃗ i − r ⃗ j ) W(\vec{r}_{i}-\vec{r}_{j}) W(ri−rj)。
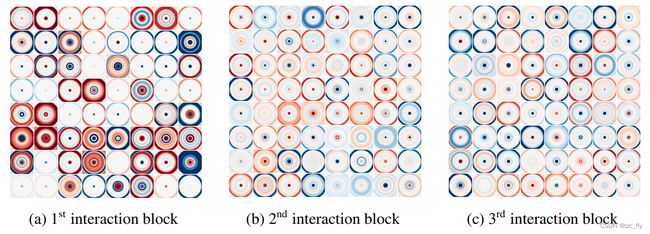
图3显示了在乙醇分子动力学轨迹上训练的SchNet的所有三个Interaction块通过生成滤波器的2d切割。可以观察每个滤波器如何强调原子间距离的特定范围。这使得它的Interaction块能够根据每个原子的径向基环境更新表示。
- 10 × 10 A ˚ 10\times 10 Å 10×10A˚切断所有64个径向。基于乙醇分子动力学训练的SchNet的每个Interaction块中的三维滤波器。负值为蓝色,正值为红色。
基于能量和力的训练
如上所述,原子间力与分子能量有关,因此可以通过将能量模型与原子位置微分得到一个能量结合力的模型: F ⃗ ^ i ( Z 1 , . . . , Z n , r ⃗ 1 , . . . , r ⃗ n ) = − ∂ E ^ ∂ r ⃗ i ( Z 1 , . . . , Z n , r ⃗ 1 , . . . , r ⃗ n ) \widehat{\vec{F}}_{i}(Z_{1},...,Z_{n},\vec{r}_{1},...,\vec{r}_{n})=-\frac{\partial \widehat{E}}{\partial\vec{r}_{i}}(Z_{1},...,Z_{n},\vec{r}_{1},...,\vec{r}_{n}) F i(Z1,...,Zn,r1,...,rn)=−∂ri∂E (Z1,...,Zn,r1,...,rn)有理论证明,这可以形成一个energy-conserving force-field。由于SchNet产生了旋转不变的能量预测,因此力的预测通过构造是旋转等变的。在训练中还包含了总能量 E E E和力 F ⃗ i \vec{F}_{i} Fi,以训练出在这两个属性上都表现良好的网络: l ( E ^ , ( E , F ⃗ 1 , . . . , F ⃗ n ) ) = ρ ∣ ∣ E − E ^ ∣ ∣ 2 + 1 n ∑ i = 0 n ∣ ∣ F ⃗ i − ( − ∂ E ^ ∂ r ⃗ i ) ∣ ∣ l(\widehat{E},(E,\vec{F}_{1},...,\vec{F}_{n}))=\rho||E-\widehat{E}||^{2}+\frac{1}{n}\sum_{i=0}^{n}||\vec{F}_{i}-(-\frac{\partial \widehat{E}}{\partial\vec{r}_{i}})|| l(E ,(E,F1,...,Fn))=ρ∣∣E−E ∣∣2+n1i=0∑n∣∣Fi−(−∂ri∂E )∣∣
实验
作者将SchNet应用于三个不同的量子化学数据集:QM9,MD17和ISO17。作者设计了这些实验,每个实验都为化学空间建模增加了另一个方面。虽然QM9只包含平衡分子,但对于MD17,作者预测了单分子分子动力学的构象变化。最后,结合化学和结构变化提出了ISO17。
对于所有数据集,报告能量的平均绝对误差为 k c a l / m o l kcal/mol kcal/mol,力的平均绝对误差为 k c a l / m o l / A ˚ kcal/mol/Å kcal/mol/A˚。在每个实验中,将数据分成给定大小为 N N N的训练集,并使用1000个样本的验证集进行早期停止。其余数据作为测试集。所有模型都使用SGD训练,使用ADAM优化器,每batch为32个分子。
小结
SchNet的优点是它不需要使用人工定义的特征来描述分子,而是自动从分子的原子坐标和类型(比如C,O,N,S,I等类型)中学习分子的特征表示。这使得它可以更准确地表示分子的物理特性,例如键长、键角和电荷等。此外,SchNet还可以处理具有不同尺度的分子结构,能够适应多种不同类型的分子问题。
SchNet是一种基于神经网络的有监督学习方法,需要使用有标注的数据进行训练。在训练SchNet时,通常需要使用量子力学计算或实验测量获得的分子属性数据作为监督信号,如分子能量、原子力等。通过最小化预测值和实际值之间的误差,可以优化模型参数,并使其能够更准确地预测分子的性质和行为。
虽然SchNet需要使用有标注的数据进行训练,但也可以使用一些无监督学习方法进行预训练,从而提高其性能。例如,可以使用自编码器或变分自编码器等无监督学习方法对分子数据进行预训练,然后将其作为SchNet的初始化参数,再使用有标注的数据进行微调,以获得更好的性能和泛化能力。