栈、队列、优先队列 - 归档
栈、队列、优先队列
概述
| 名词 | 性质 |
|---|
栈
20. Valid Parentheses*(栈简单应用1)
150. Evaluate Reverse Polish Notation*(栈的简单应用2)
71. Simplify Path*
------------栈和树(递归)的关系、系统栈原理、模拟系统栈的非递归遍历-------------------
144. Binary Tree Preorder Traversal**(模拟系统栈)
94. Binary Tree Inorder Traversal**(模拟系统栈)
145. Binary Tree Postorder Traversal**(模拟系统栈)
341. Flatten Nested List Iterator***(系统设计,DFS遍历嵌套列表)
队列
应用:广度优先遍历
--------------------------------------树 - 层序遍历------------------------------------------------------
102. Binary Tree Level Order Traversal*
107. Binary Tree Level Order Traversal II*
103. Binary Tree Zigzag Level Order Traversal*
199. Binary Tree Right Side View*
------------------------------------图 - 无权图最短路径的建模(有权图用什么算法)------------------------------
279. Perfect Squares***(BFS建模 / DP建模)
是否有无解的情况?是否可以用贪心?
12 = 9 + 1 + 1 + 1
12 = 4 + 4 + 4
BFS的关联?如何将题意建模转化为图论的问题?
DP? 如何将题意建模转化为DP的问题?
127. Word Ladder***
126. Word Ladder II****(保存路径用DFS)
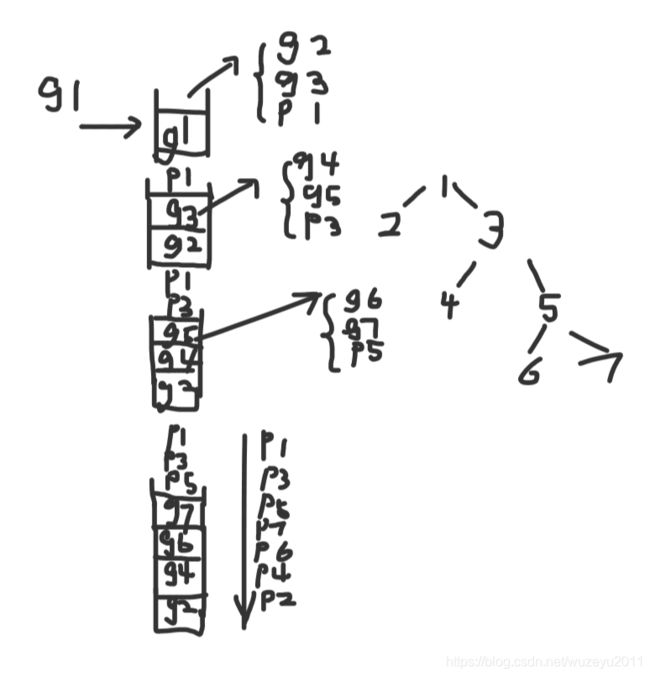
优先队列
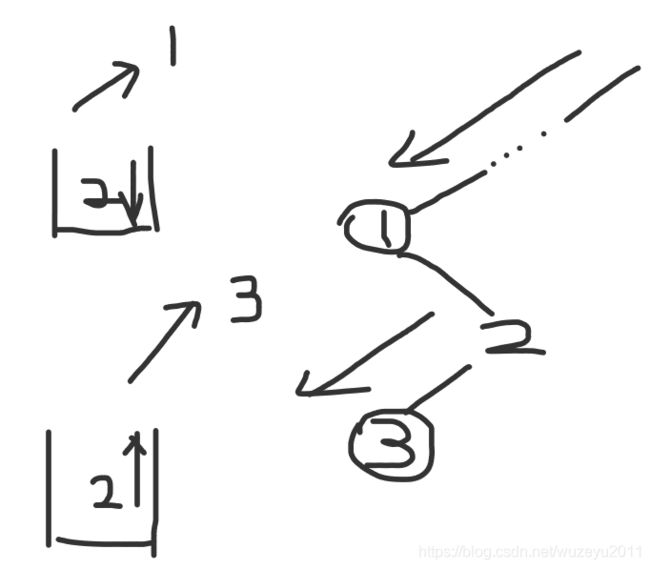
优先队列 - 堆的底层结构(数组模拟一棵树)
347. Top K Frequent Elements***(用优先队列容器)
23. Merge k Sorted Lists**(和347一样)
692. Top K Frequent Words**(和347一样)
------------------------------------------------------------------
------------------------------------------------------------------
------------------------------------------------------------------
20. Valid Parentheses
- 栈的初级使用
- hash表用作括号对的匹配
class Solution {
public:
bool isValid(string s) {
if(s.empty())
return true;
map<char,char> cMap{{')', '('}, { ']', '['}, {'}', '{'}};
stack<char> cStack;
for(int i = 0; i < s.size(); i++){
if(s[i] == '(' || s[i] == '[' || s[i] =='{')
cStack.push(s[i]);
else{
if(cStack.empty())
return false;
if(cStack.top() == cMap[s[i]])
cStack.pop();
else
return false;
}
}
return cStack.empty();
}
};
150. Evaluate Reverse Polish Notation

栈的应用,哈希表主要为了switch case无法判别字符:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
int a;
int b;
for(int i = 0; i < tokens.size(); i++){
if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){
a = st.top();
st.pop();
b = st.top();
st.pop();
st.push(operate(a, b, tokens[i]));
}
else
st.push(atoi(tokens[i].c_str()));
}
return st.top();
}
private:
map<string, int> imap{{"+", 1}, {"-", 2}, {"*", 3}, {"/", 4}};
int operate(int& a, int& b, string& opt){
int iret;
switch(imap[opt]){
case 1:
iret = a + b;
break;
case 2:
iret = b - a;
break;
case 3:
iret = a * b;
break;
case 4:
iret = b / a;
break;
}
return iret;
}
};
71. Simplify Path
- 注意split的用法,c++里面没有split…,这里在for循环里面构建path.split(’/’)的每个部分 string s.
class Solution {
public:
string simplifyPath(string path) {
//用‘/’将path进行分割,或者说过滤掉path中所有的‘/’,提取两侧是字符串到vsting中。
vector<string> vstring;
string ret;
for(int i = 0; i < path.size(); i++){
while(i < path.size() && path[i] == '/')
i++;
int start = i;
if(start == path.size())
break;
while(i < path.size() && path[i] != '/')
i++;
int end = i - 1;
string s = path.substr(start, end - start + 1);
if(s == ".."){
if(!vstring.empty())
vstring.pop_back();
}
else if( s != ".")
vstring.push_back(s);
}
if(vstring.empty())
return "/";
for(auto& s : vstring)
ret += '/' + s;
return ret;
}
};
144. Binary Tree Preorder Traversal
前序遍历
- 递归
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if(root == NULL){
return ret;
}
ret.push_back(root->val);
preorderTraversal(root->left);
preorderTraversal(root->right);
return ret;
}
private:
vector<int> ret;
};
- 栈的DFS
栈的大小不代表递归的深度。
出栈作为栈顶节点(根节点)进行访问,按照右左次序将子节点入栈。循环以上的操作。
操作之间,会将上次入栈的右孩子保留在栈中,直到所有左节点全部出栈访问完毕,才开始访问这个右孩子节点,很好的符合了前序遍历 root、root->left、root->right的访问次序。

class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
if(root == NULL){
return ret;
}
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
ret.push_back(node->val);
st.pop();
if(node->right)
st.push(node->right);
if(node->left)
st.push(node->left);
}
return ret;
}
};
- 栈模拟系统栈
栈中存放元素:
struct Command {
string s;
TreeNode* node;
Command(string s, TreeNode* node) : s(s), node(node) {}
};
和第二种方法比较:
st.push(Command(“print”, c.node)),访问某个节点时不急着打印,将打印命令入栈,与左右节点访问入栈一起在栈中形成前中后序关系。这样方便前中后序中,遍历操作于当前节点打印进行逻辑组合,代码形式上也更简洁。
ret.push_back(node->val);
直接弹出打印栈顶节点,这样打印的顺序依赖于弹栈后左右节点入栈顺序。(这个形式只适合前后序遍历,中序不行)
TreeNode* node = st.top();
ret.push_back(node->val);
st.pop();
if(node->right)
st.push(node->right);
if(node->left)
st.push(node->left);
if(c.node->right)
st.push(Command("go", c.node->right));
if(c.node->left)
st.push(Command("go", c.node->left));
st.push(Command("print", c.node));
if(c.node->right)
st.push(Command("go", c.node->right));
st.push(Command("print", c.node));
if(c.node->left)
st.push(Command("go", c.node->left));
st.push(Command("print", c.node));
if(c.node->right)
st.push(Command("go", c.node->right));
if(c.node->left)
st.push(Command("go", c.node->left));
struct Command {
string s;
TreeNode* node;
Command(string s, TreeNode* node) : s(s), node(node) {}
};
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
stack<Command> st;
if(root == NULL)
return ret;
st.push(Command("go", root));
while(!st.empty()){
Command c = st.top();
st.pop();
if(c.s == "go"){
if(c.node->right)
st.push(Command("go", c.node->right));
if(c.node->left)
st.push(Command("go", c.node->left));
st.push(Command("print", c.node));
}
else if(c.s == "print")
ret.push_back(c.node->val);
}
return ret;
}
};
94. Binary Tree Inorder Traversal
- 递归
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if(root == NULL){
return ret;
}
inorderTraversal(root->left);
ret.push_back(root->val);
inorderTraversal(root->right);
return ret;
}
private:
vector<int> ret;
};
- 栈的DFS
栈的大小不代表递归的深度。
整棵树从左往右访问。
入栈的都作为根节点,出栈作为:
右孩为空,它是左节点,下次访问根节点。
右孩不为空,它是根节点,下次访问右树。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
while(!st.empty() || root){
while(root){
st.push(root);
root = root->left;
}
ret.push_back(st.top()->val);
root = st.top()->right;
st.pop();
}
return ret;
}
};
- 栈模拟系统栈
if(c.s == "go"){
if(c.node->right)
st.push(Command("go", c.node->right));
st.push(Command("print", c.node));
if(c.node->left)
st.push(Command("go", c.node->left));
}
else if(c.s == "print")
ret.push_back(c.node->val);
145. Binary Tree Postorder Traversall
- 递归
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if(root == NULL){
return ret;
}
postorderTraversal(root->left);
postorderTraversal(root->right);
ret.push_back(root->val);
return ret;
}
private:
vector<int> ret;
};
- 栈
栈的大小不代表递归的深度。
前序遍历的逆序输出(前序的基础上,调整了前序左右子树的访问顺序得到非标准的前序遍历,然后再将返回数组逆序输出得到标准的后序遍历)
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ret;
stack<TreeNode*> st;
if(root == NULL){
return ret;
}
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
ret.push_back(node->val);
st.pop();
if(node->left) st.push(node->left);
if(node->right) st.push(node->right);
}
std::reverse(ret.begin(), ret.end());
return ret;
}
};
- 栈
栈的大小不代表递归的深度。
在这里插入代码片
- 栈模拟系统栈
if(c.s == "go"){
st.push(Command("print", c.node));
if(c.node->right)
st.push(Command("go", c.node->right));
if(c.node->left)
st.push(Command("go", c.node->left));
}
else if(c.s == "print")
ret.push_back(c.node->val);
341. Flatten Nested List Iterator
典型DFS用在嵌套的列表中:
class NestedIterator {
public:
NestedIterator(vector<NestedInteger> &nestedList) {
helper(nestedList);
it = flatten.begin();
}
int next() {
return *it++;
}
bool hasNext() {
if(it >= flatten.end())
return false;
else
return true;
}
private:
void helper(vector<NestedInteger> &nestedList) {
for(auto& nested :nestedList){
if(nested.isInteger())
flatten.push_back(nested.getInteger());
else
helper(nested.getList());
}
}
vector<int> flatten;
vector<int>::iterator it;
};
102. Binary Tree Level Order Traversal
队列辅助的层序遍历
- 入队元素需要记录所在的level: pair
- 出队到下一层时,需要push存放下一层节点的数组:if(nodeLevel == ret.size()) ret.push_back(vector());
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
queue<pair<TreeNode*, int>> q;
if(root == NULL)
return ret;
q.push(make_pair(root, 0));
while(!q.empty()){
TreeNode* frontNode = q.front().first;
int nodeLevel = q.front().second;
q.pop();
if(nodeLevel == ret.size())
ret.push_back(vector<int>());
ret[nodeLevel].push_back(frontNode->val);
if(frontNode->left)
q.push(make_pair(frontNode->left, nodeLevel + 1));
if(frontNode->right)
q.push(make_pair(frontNode->right, nodeLevel + 1));
}
return ret;
}
};
第二种队列辅助的层序遍历
3. 每层都在for : nums循环中遍历,每层遍历结束后当前层已经出队,下一层已经入队,下一层节点个数等于:nums = q.size();
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
vector<int> level;
queue<TreeNode*> q;
int nums = 0;
if(root == NULL)
return ret;
q.push(root);
while(!q.empty()){
nums = q.size();
for(int i = 0; i < nums; i++){
TreeNode* frontNode = q.front();
q.pop();
level.push_back(frontNode->val);
if(frontNode->left)
q.push(frontNode->left);
if(frontNode->right)
q.push(frontNode->right);
}
ret.push_back(level);
level.clear();
}
return ret;
}
};
- 递归DFS
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
if(root == NULL)
return ret;
helper(root, ret, 0);
return ret;
}
private:
void helper(TreeNode* node, vector<vector<int>>& ret, int level){
if(ret.size() == level)
ret.push_back(vector<int>());
ret[level].push_back(node->val);
if(node->left) helper(node->left, ret, level + 1);
if(node->right) helper(node->right, ret, level + 1);
}
};
107. Binary Tree Level Order Traversal II
102题的返回值,reverse即可:
std::reverse(ret.begin(), ret.end());
return ret;
103. Binary Tree Zigzag Level Order Traversal
- BFS, 添加参数level判断当前行是否是需要逆序的做reverse操作。
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret;
//q 出队更新每一层的vlevel
vector<int> vlevel;
queue<TreeNode*> q;
int nums = 0;
int level = 0;
if(root == NULL)
return ret;
q.push(root);
while(!q.empty()){
nums = q.size();
for(int i = 0; i < nums; i++){
TreeNode* frontNode = q.front();
q.pop();
vlevel.push_back(frontNode->val);
if(frontNode->left)
q.push(frontNode->left);
if(frontNode->right)
q.push(frontNode->right);
}
if(level % 2){
std::reverse(vlevel.begin(), vlevel.end());
ret.push_back(vlevel);
}
else
ret.push_back(vlevel);
vlevel.clear();
level++;
}
return ret;
}
};
- BFS可以使用双端队列实现。
xxx
- 看题解的时候,发现层序遍历除了基于队列的BFS,也可以用DFS实现
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret;
if(root == NULL)
return ret;
helper(root, ret, 0);
return ret;
}
private:
void helper(TreeNode* node, vector<vector<int>>& ret, int level){
if(ret.size() == level)
ret.push_back(vector<int>());
if(level % 2)
ret[level].insert(ret[level].begin(), node->val);
else
ret[level].push_back(node->val);
if(node->left) helper(node->left, ret, level + 1);
if(node->right) helper(node->right, ret, level + 1);
}
};
199. Binary Tree Right Side View
- DFS
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<vector<int>> temp;
vector<int> ret;
if(root == NULL)
return ret;
helper(root, temp, 0);
//再取每一行的最后一个节点
for(auto& vLevel : temp)
ret.push_back(*(vLevel.end() - 1));
return ret;
}
private:
void helper(TreeNode* node, vector<vector<int>>& ret, int level){
if(ret.size() == level)
ret.push_back(vector<int>());
ret[level].push_back(node->val);
if(node->left) helper(node->left, ret, level + 1);
if(node->right) helper(node->right, ret, level + 1);
}
};
- BFS
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> q;
vector<int> ret;
int row = 0;
if(root == NULL)
return ret;
q.push(root);
while(!q.empty()){
row = q.size();
for(int i = 0; i < row; i++){
TreeNode* node = q.front();
q.pop();
if(i == row - 1)
ret.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
}
return ret;
}
};
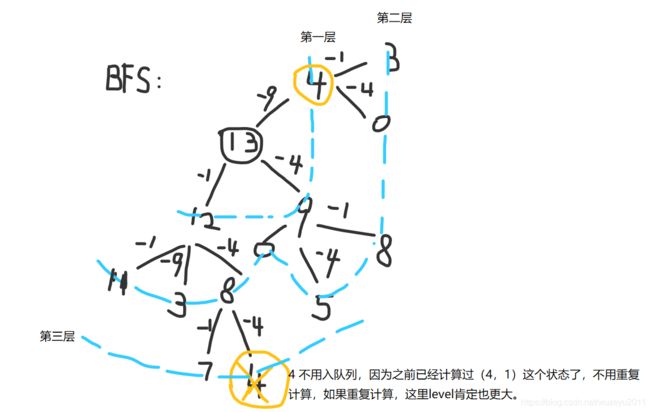
279. Perfect Squares

BFS, 每层元素都携带本层的层数level:
res: 本节点剩余值, level: 本节点所在层
queue
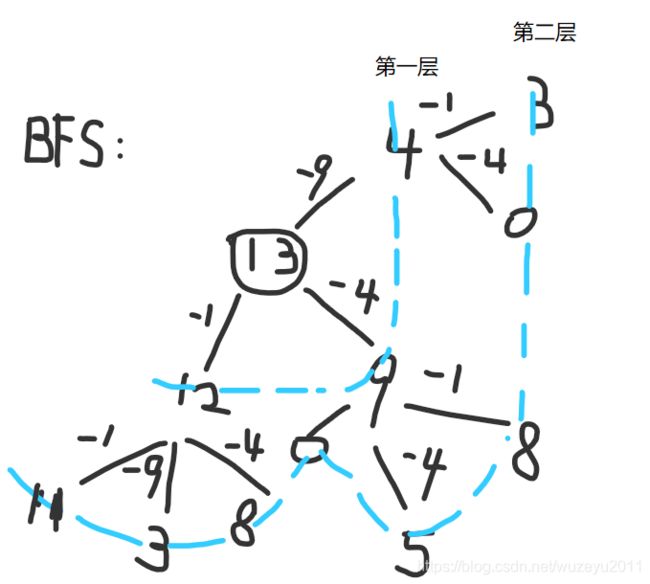
- 遍历完每层所有可能性
class Solution {
public:
int numSquares(int n) {
queue<pair<int, int>> q;
int least = 0;
q.push(make_pair(n, 0));
while(!q.empty()){
pair<int, int> front = q.front();
q.pop();
//cout << "pop:" << front.first <<" level:" << front.second;
for(int i = 1; front.first - i*i >= 0; i++){
//cout <<" res:" << front.first - i*i << " ";
if(front.first - i*i == 0)
return ++front.second;
int res = front.first - i*i;
q.push(make_pair(res, front.second + 1));
}
//cout << endl;
}
return 0;
}
};
class Solution {
public:
int numSquares(int n) {
queue<pair<int, int>> q;
int least = 0;
vector<bool> memo(n, false);
q.push(make_pair(n, 0));
while(!q.empty()){
pair<int, int> front = q.front();
q.pop();
for(int i = 1; front.first - i*i >= 0; i++){
if(front.first - i*i == 0)
return ++front.second;
int res = front.first - i*i;
if(memo[res])
continue;
q.push(make_pair(res, front.second + 1));
memo[res] = true;
}
}
return 0;
}
};
- 动态规划
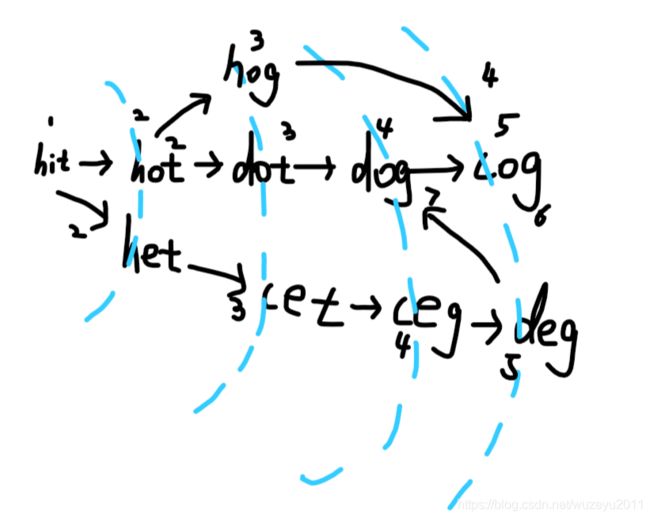
127. Word Ladder
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
queue<pair<string, int>> q;
vector<bool> popList(wordList.size(), false);
string s;
int level = 0;
q.push(make_pair(beginWord, 1));
while(!q.empty()){
s = q.front().first;
level = q.front().second;
q.pop();
if(s == endWord)
return level;
level++;
for(int i = 0; i < wordList.size(); i++){
if(popList[i])
continue;
if(isConnected(s, wordList[i])){
q.push(make_pair(wordList[i], level));
popList[i] = true;//删除掉已经入队或者出队的节点,防止重复遍历到(形成环)
}
}
}
return 0;
}
private:
bool isConnected(string& a, string& b){
int isConnected = 0;
for(int i = 0; i < a.size(); i++){
if(a[i] != b[i])
isConnected += 1;
}
return isConnected == 1;
}
};
- 加入hashtable优化时间复杂度, 搜索临节点效率改善为:26 * wordsize
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
queue<pair<string, int>> q;
unordered_set<string> set;
for(auto& word : wordList){
set.insert(word);
}
string s;
int level = 0;
q.push(make_pair(beginWord, 1));
while(!q.empty()){
s = q.front().first;
level = q.front().second;
q.pop();
//寻找到与s相邻的节点,标记为level++,并且加入队列
int ret = pushQueue(q, set, s, endWord, ++level);
if(ret)
return ret;
}
return 0;
}
private:
int pushQueue(queue<pair<string, int>>& q, unordered_set<string>& set, string& s, string& endWord, int level){
for(int i = 0; i < s.size(); i++){
for(char c = 'a'; c <= 'z'; c++){
char temp = s[i];
if(temp == c)
continue;
s[i] = c;
if(set.find(s) != set.end()){
//搜索到目标节点,则直接返回,不用入队了。
//可能会节约遍历一层的时间。
if(s == endWord)
return level;
q.push(make_pair(s, level));
//删除掉已经入队或者出队的节点,防止重复遍历到(形成环)
set.erase(s);
}
s[i] = temp;
}
}
return 0;
}
};
- DFS?
在这里插入代码片
126. Word Ladder II
347. Top K Frequent Elements
- 优先队列:priority_queue
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int/*数值*/, int/*频率*/> freqMap;
priority_queue<pair<int/*频率*/, int/*数值*/>, std::vector<pair<int, int>>, greater<pair<int, int>>> minHeap;
for(auto& val : nums){
freqMap[val]++;
}
for(auto& pair : freqMap){
if(k == minHeap.size()){
if(pair.second > minHeap.top().first){
minHeap.pop();
minHeap.push(make_pair(pair.second, pair.first));
}
}
else
minHeap.push(make_pair(pair.second, pair.first));
}
vector<int> ret;
while(!minHeap.empty()){
ret.push_back(minHeap.top().second);
minHeap.pop();
}
return ret;
}
};
23. Merge k Sorted Lists
- 套用347题代码,堆内保存数据个数为k个链表中所有不相同的元素。.
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
unordered_map<int/*数值*/, int/*频率*/> freqMap;
priority_queue<pair<int,int>, std::vector<pair<int,int>>, greater<pair<int,int>>> minHeap;
for(auto pList : lists){
ListNode* pHead = pList;
while(pHead){
freqMap[pHead->val]++;
pHead = pHead->next;
}
}
for(auto& pair : freqMap){
minHeap.push(make_pair(pair.first, pair.second));
}
ListNode* ListHead = new ListNode(0);
ListNode* Node = ListHead;
while(!minHeap.empty()){
int val = minHeap.top().first;
int rep = minHeap.top().second;
while(rep--){
Node->next = new ListNode(val);
Node = Node->next;
}
minHeap.pop();
}
return ListHead->next;
}
};
- 优化?
692. Top K Frequent Words
class Solution {
public:
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string, int> freqMap;
//Comparator自定义的小堆,保存前k个出现频次最高的元素,队首是小元素
priority_queue<pair<int, string>, vector<pair<int, string>>, Comparator> minHeap;
for(auto& s : words){
freqMap[s]++;
}
for(auto& pair : freqMap){
if(k == minHeap.size()){
if(pair.second > minHeap.top().first || (pair.second == minHeap.top().first && pair.first < minHeap.top().second)){
minHeap.pop();
minHeap.push(make_pair(pair.second, pair.first));
}
}
else{
minHeap.push(make_pair(pair.second, pair.first));
}
}
vector<string> ret;
while(!minHeap.empty()){
ret.push_back(minHeap.top().second);
minHeap.pop();
}
//将最大元素放置到首位来
reverse(ret.begin(), ret.end());
return ret;
}
private:
struct Comparator {
bool operator()(pair<int, string>& ls, pair<int, string>& rs)
{
return ls.first == rs.first ?
ls.second < rs.second : // 频率一致,字母顺序小的大
ls.first > rs.first;
}
};
};