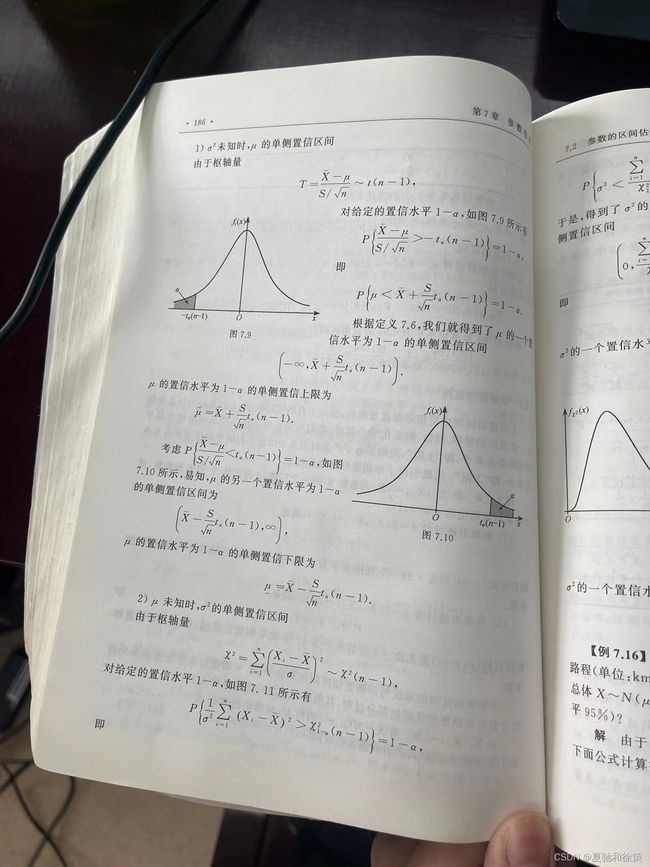
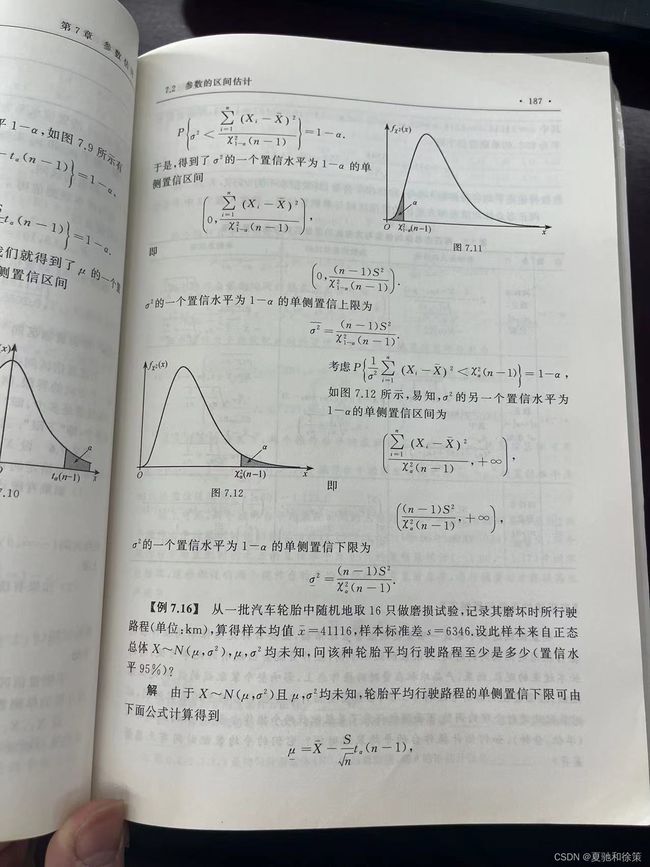
7.2 参数区间的估计
学习目标:
要学习参数的区间估计,我会采取以下步骤:
-
学习理论知识:首先,我会学习与参数的区间估计相关的理论知识,包括置信区间、抽样分布、中心极限定理、样本容量对置信区间的影响等。
-
掌握计算方法:掌握计算参数置信区间的方法是学习参数区间估计的关键。对于不同的参数估计方法,可能有不同的置信区间计算公式,需要学习如何应用这些公式来计算置信区间。
-
理解实际应用:对于实际问题,我会理解如何使用参数置信区间来解决实际问题,例如如何确定置信水平、如何解释置信区间、如何进行假设检验等。
-
实践练习:学习理论知识和计算方法后,我会进行实践练习,例如使用R或Python等工具进行统计分析实验,尝试计算参数的置信区间,理解置信区间的含义,以及如何解释和应用这些结果。
-
持续学习:学习参数的区间估计需要持续学习和练习,以便在实际问题中灵活应用统计方法,提高数据分析的准确性和可靠性。
总之,学习参数的区间估计需要掌握理论知识和计算方法,理解实际应用,进行实践练习,以及持续学习和练习。
解释:
区间估计是一种统计推断方法,用于通过样本数据推断总体参数的估计区间。区间估计是基于样本数据来估计总体参数,由于样本数据的随机性,同样的样本数据可能导致不同的参数估计值。因此,区间估计给出的是总体参数的估计范围,而不是一个确定的点估计值。
在区间估计中,我们通常使用置信区间来描述总体参数的估计范围。置信区间是指总体参数在一定置信水平下的估计范围。例如,如果我们使用95%的置信水平,表示在100次抽样中,有95次的置信区间会覆盖总体参数的真实值。置信区间的长度与样本容量和置信水平有关。样本容量越大、置信水平越高,置信区间越窄,表示我们对总体参数的估计越准确。
区间估计的应用非常广泛,例如在医学、社会科学、经济学等领域中,我们需要通过样本数据估计总体参数,如平均值、方差、比例等。通过区间估计,我们可以给出总体参数的估计范围,帮助我们进行决策和判断,从而更好地理解数据并做出科学的决策。
我的理解:
区间估计是一种基于样本数据对总体参数进行估计的方法,其目的是为了对总体参数的未知真实值提供一个范围估计。具体来说,区间估计就是给出一个区间,该区间的两个端点是由样本数据计算得出的统计量,而这个区间有一定的概率包含总体参数的真实值。这个概率被称为置信水平,通常是以95%或者99%的概率进行估计。
可以举个简单的例子来理解区间估计的概念。
假设我们要估计一群学生的平均身高,但是我们不能测量每个学生的身高,因此我们随机抽取了20名学生的身高作为样本数据。通过计算这20名学生身高的平均值和标准差,我们可以得到一个平均身高的区间估计。如果我们选择了95%的置信水平,那么我们可以得到一个区间,该区间的两个端点是由样本数据计算出来的,这个区间有95%的概率包含总体平均身高的真实值。在实际应用中,我们通常使用区间估计来描述总体参数的不确定性,并根据置信区间的宽度来评估参数估计的精度和可靠性。
 上文解释:
上文解释:
总体均值的区间估计是指通过样本数据来估计总体均值的一个范围区间,这个范围区间是由样本统计量计算得出的,并且有一定的概率包含总体均值的真实值。总体均值的区间估计通常采用t分布或者正态分布进行计算。
总体均值的区间估计的步骤如下:
-
确定置信水平:通常我们会选择95%或者99%的置信水平。
-
选择样本数据并计算样本均值和标准差:根据样本数量和采样方式,我们可以选择不同大小的样本数据。样本均值是样本数据的平均值,样本标准差是样本数据的标准差。
-
计算标准误差:标准误差是样本均值的标准差,可以用样本标准差除以样本大小的平方根得到。
-
计算置信区间:根据所选置信水平和样本数据的大小,可以用t分布或者正态分布计算出置信区间。在使用t分布计算置信区间时,需要注意样本数据的大小是否足够大,如果样本数据的大小小于30,则需要使用t分布来计算置信区间;如果样本数据的大小大于等于30,则可以使用正态分布来计算置信区间。
总体均值的区间估计可以帮助我们了解总体均值的不确定性,并根据置信区间的宽度来评估参数估计的精度和可靠性。当置信区间越窄,估计结果越精确,估计误差也越小。
我的理解:
总体均值的区间估计可以帮助我们了解总体均值的不确定性。在实际应用中,我们很难获得总体的全部数据,因此只能通过对样本数据进行统计分析来推断总体的性质。通过计算样本均值和标准差,我们可以估计总体均值和标准差的值。但是,样本均值和标准差是从样本数据中随机选择得到的,因此可能与总体均值和标准差略有不同。这就需要通过区间估计来估计总体均值的范围,以便了解总体均值的真实值可能在哪个范围内。
区间估计给出了一个包含总体均值的范围,这个范围有一定的概率包含总体均值的真实值。置信水平是衡量区间估计可靠性的一个指标。比如,95%的置信水平意味着在多次采样和估计的过程中,有95%的情况下这个区间包含了总体均值的真实值。在进行区间估计时,我们需要选择置信水平和样本数据的大小,并根据样本数据的均值、标准差和样本数量来计算置信区间的端点。
总体均值的区间估计在很多实际应用中都有着广泛的应用,比如在医学、金融、市场调查等领域。它可以帮助我们了解总体均值的不确定性,进而为决策提供可靠的依据。
上文解释:
正态总体方差的区间估计也是一个常见的统计推断问题。正态总体是指总体的分布服从正态分布,因此正态总体方差的区间估计方法与总体均值的区间估计方法有所不同。正态总体方差的区间估计需要利用样本方差、样本数量和卡方分布的性质来计算置信区间的端点。
一般来说,我们通过样本方差来估计总体方差。但是样本方差通常会低估总体方差,因此需要对样本方差进行调整。具体来说,我们使用样本方差除以自由度的修正因子,得到一个新的统计量,称为修正后的样本方差。自由度是指样本中独立观测值的个数减去1,可以通过样本数量减去1来计算。修正后的样本方差更接近总体方差的真实值,因此可以更准确地进行区间估计。
正态总体方差的区间估计同样需要选择置信水平和样本数据的大小,并根据样本数据的修正后的样本方差和自由度来计算置信区间的端点。置信区间的上下限可以通过查找卡方分布的表格或使用统计软件来计算。常见的置信水平是95%和99%。
总之,正态总体方差的区间估计可以帮助我们了解总体方差的不确定性,进而为决策提供可靠的依据。需要注意的是,在样本数量较小的情况下,使用卡方分布进行区间估计可能会存在较大的误差,因此需要谨慎使用。
我的理解:
正态总体方差的区间估计是指,对于一个满足正态分布假设的总体,根据从中抽取的样本数据,利用统计方法来计算总体方差的一个置信区间,该区间包含总体方差的真实值的概率达到预先设定的置信水平。
通常情况下,我们无法直接获得总体方差的真实值,因此需要利用样本数据来估计总体方差。但是由于样本数据是有限的,估计出来的总体方差往往与真实值存在偏差,因此需要利用置信区间来衡量估计值的不确定性。
具体来说,我们可以根据样本数据计算样本方差,然后根据样本数量和自由度(样本数量减1)计算修正后的样本方差。利用修正后的样本方差和自由度,我们可以通过查找卡方分布表或使用统计软件计算出置信区间的上下限。常见的置信水平是95%和99%。
正态总体方差的区间估计在实际应用中十分重要。例如,在质量控制和产品检验领域,我们需要对产品的尺寸、重量、硬度等指标的方差进行估计,以便评估产品的稳定性和可靠性。通过正态总体方差的区间估计,我们可以判断产品指标方差的大小,进而优化生产工艺、改进产品设计等。
上文解析:
两正态总体均值差的区间估计是指,对于两个满足正态分布假设的总体,根据从中抽取的样本数据,利用统计方法来计算两总体均值差的一个置信区间,该区间包含两总体均值差的真实值的概率达到预先设定的置信水平。
具体来说,假设我们有两个正态总体 X和 Y,其均值分别为 \mu_X 和 \mu_Y,方差分别为 \sigma_X^2 和 \sigma_Y^2。我们从两个总体中分别抽取大小为 n_1 和 n_2 的独立样本,样本均值分别为 \bar{X}和 $bar{Y},样本标准差分别为 S_X 和 S_Y。假设两个总体的方差相等,则可以使用学生 t 分布来计算均值差的置信区间。如果方差不相等,则需要使用 Welch t 分布。
使用学生 t 分布时,我们需要计算样本均值差 \bar{X} - \bar{Y}和标准误差 SE(\bar{X} - \bar{Y}),然后根据置信水平、自由度(n_1 + n_2 - 2)和 t 分布的概率密度函数,查找 t 分布表或使用统计软件来计算置信区间的上下限。
使用 Welch t 分布时,我们需要计算 Welch-Satterthwaite 方程来估计自由度,然后按照上述方法计算置信区间。
两正态总体均值差的区间估计在实际应用中非常重要。例如,在医学和生物统计学领域,我们需要比较两个治疗方案或两个人群的平均数值,以评估它们之间的差异性。通过两正态总体均值差的区间估计,我们可以判断两总体均值差的大小和方向,进而制定合理的决策和行动计划。
我的理解:
两正态总体均值差的区间估计,是指对于两个服从正态分布的总体,通过从两个总体中抽取的样本数据,利用统计学方法估计这两个总体的均值之差,并且通过置信区间来判断均值差的大小和方向。
在实际应用中,我们经常需要比较两个总体的均值差异,例如比较两种治疗方法的疗效,或者比较两个厂家的生产工艺的差异等。在这些应用场景下,我们往往需要从两个总体中分别抽取样本,然后计算样本均值,再通过统计方法来估计总体均值之差,并且构造置信区间来衡量这个差异的显著性和可信度。
具体地,对于两个服从正态分布的总体,我们可以从这两个总体中分别抽取样本,并分别计算出样本均值和样本标准差。接下来,我们可以计算样本均值的差值和它的标准误差,然后利用t分布来构造置信区间,得到总体均值差的一个区间估计。如果两个总体方差相等,我们可以使用学生t分布进行区间估计;如果方差不相等,我们需要使用Welch t分布来进行区间估计。
两正态总体均值差的区间估计在实际应用中非常重要,它可以帮助我们判断两个总体之间的差异是否显著,并且提供了一个可靠的依据来进行决策。
上文解析:
两正态总体方差比的区间估计是指在给定两个服从正态分布的总体的样本方差的情况下,通过统计学方法估计两个总体的方差比,并构造置信区间来估计该比值的精度和可信度。
在实际应用中,我们经常需要比较两个总体的方差差异,例如比较两种设备测量结果的精度、比较两个工艺生产的质量差异等。而两个总体的方差比是非常重要的参数之一,在许多统计模型中也是必要的参数。因此,需要对两个总体的方差比进行区间估计,以便判断差异是否显著并且获得更准确的模型参数估计。
具体地,对于两个服从正态分布的总体,我们可以从这两个总体中分别抽取样本,并计算出样本的方差。然后,我们可以计算两个总体方差的比值,并通过F分布来构造置信区间,得到总体方差比的一个区间估计。在实际应用中,由于F分布的特殊性质,我们通常将置信区间表示为样本方差比的倒数,从而更容易进行计算和解释。
需要注意的是,对于两个总体方差比的区间估计,我们需要满足一些假设前提,如正态性、方差齐性等。同时,在计算置信区间时,还需要考虑样本大小和显著性水平等因素,以确保估计结果的准确性和可靠性。
总之,两正态总体方差比的区间估计在许多领域中都有重要应用,如质量控制、医学研究、工程实验等,能够帮助我们判断两个总体方差是否有显著差异,并为模型参数的准确估计提供重要依据。
我的理解:
两正态总体方差比的区间估计是指在给定两个服从正态分布的总体的样本方差的情况下,通过统计学方法估计两个总体的方差比,并构造置信区间来估计该比值的精度和可信度。
简单来说,我们通过收集两个服从正态分布的总体的样本数据,计算样本的方差,然后使用统计学方法计算出两个总体的方差比,最后通过置信区间来估计方差比的精度和可信度。这个估计过程可以帮助我们比较两个总体的方差差异,从而得出更可靠的结论。
需要注意的是,为了进行方差比的区间估计,我们需要满足一些假设前提,例如两个总体都是正态分布、样本方差是独立的、两个总体的方差是齐性的等。同时,在计算置信区间时,还需要考虑样本大小、显著性水平和自由度等因素,以确保估计结果的准确性和可靠性。
总之,两正态总体方差比的区间估计是一个非常重要的统计学方法,在实际应用中被广泛使用。它能够帮助我们比较两个总体的方差差异,从而得出更准确的结论。
 我的解释:
我的解释:
单侧置信区间是指在进行参数估计时,只考虑某一方向的误差,例如上限或下限。与双侧置信区间不同,单侧置信区间只考虑一个方向的置信度,通常用于需要限制某一方向误差的情况。
在实际应用中,单侧置信区间通常会用于判断某个样本是否符合某个要求或标准,例如检验产品尺寸是否符合标准。如果我们希望限制样本尺寸的上限,我们可以使用单侧置信区间来估计尺寸的最大值,并判断是否超出了标准。
计算单侧置信区间的方法和双侧置信区间类似,不同的是在计算置信区间的时候只考虑一个方向。例如,我们可以根据样本数据和置信度,计算出某个参数的下限置信区间或上限置信区间,并根据实际需要进行判断和应用。
需要注意的是,单侧置信区间通常要比双侧置信区间更具有特定的应用场景,例如需要限制某一方向误差或仅关心某一方向的统计学特征时。同时,在使用单侧置信区间进行参数估计时,也需要注意样本量的大小和显著性水平等因素,以确保估计结果的准确性和可靠性。
我的理解:
单侧置信区间是指在进行参数估计时,只考虑某一方向的误差,例如上限或下限。与双侧置信区间不同,单侧置信区间只考虑一个方向的置信度,通常用于需要限制某一方向误差的情况。
在实际应用中,单侧置信区间通常会用于判断某个样本是否符合某个要求或标准,例如检验产品尺寸是否符合标准。如果我们希望限制样本尺寸的上限,我们可以使用单侧置信区间来估计尺寸的最大值,并判断是否超出了标准。
计算单侧置信区间的方法和双侧置信区间类似,不同的是在计算置信区间的时候只考虑一个方向。例如,我们可以根据样本数据和置信度,计算出某个参数的下限置信区间或上限置信区间,并根据实际需要进行判断和应用。
需要注意的是,单侧置信区间通常要比双侧置信区间更具有特定的应用场景,例如需要限制某一方向误差或仅关心某一方向的统计学特征时。同时,在使用单侧置信区间进行参数估计时,也需要注意样本量的大小和显著性水平等因素,以确保估计结果的准确性和可靠性。
 总结:
总结:
参数的区间估计是统计学中重要的概念之一,其主要目的是通过样本数据对总体参数进行估计,并给出估计结果的可靠区间。以下是参数的区间估计的重点、难点和易错点:
重点:
- 理解置信水平的概念,即给出的区间估计有多大的概率包含总体参数真实值;
- 确定适当的置信水平和样本大小,以保证所得的区间估计具有一定的可靠性;
- 熟悉常见的分布类型(例如正态分布、t分布、F分布等)以及它们在区间估计中的应用;
- 掌握计算区间估计的公式和步骤,包括点估计、标准误差、置信度水平等指标的计算方法。
难点:
- 确定置信度水平的大小,需要权衡区间估计的精度和置信度;
- 样本的大小和样本的分布情况会影响区间估计的精度,因此需要考虑适当的样本量和样本选取方法;
- 对于不同类型的参数,需要根据不同的分布类型和假设条件选择适当的区间估计方法;
- 区间估计结果的解释需要注意置信度水平和置信区间的含义,避免出现误解或歧义。
易错点:
- 对置信度水平和置信区间的概念理解不清,导致误解区间估计结果;
- 在计算标准误差和置信区间时,误用样本标准差代替总体标准差,导致结果不准确;
- 对于不同类型的参数,选择不恰当的分布类型和假设条件,导致区间估计不准确;
- 在解释区间估计结果时,忽略置信度水平的影响,误解区间估计结果的精度和置信度。