LeetCode岛屿问题通用解决模板
文章目录
- 前言
- 第一题:求岛屿的周长
- 模板整理
-
- 遍历方向
- 确定边界
- 重复遍历问题处理
- 模板解第一题
- 第二题:求岛屿数量
- 第三题:岛屿的最大面积
- 第四题:统计子岛屿
- 第五题:统计封闭岛屿的数目
- 第六题:最大人工岛
- 总结
前言
岛屿类问题,最简单的处理方式就是使用深度优先遍历来解,找到一个陆地后,不断的向其上下左右四个方向进行遍历,直到抵达边界或者水域为止。
我们先从一道LeetCode上的题目了解一下一般岛屿类题目的问题场景。
第一题:求岛屿的周长
模板整理
首先按照深度优先遍历的思想,肯定是先找到遍历的方式,一般网格类,我们可以按照上下左右四个方向进行遍历,再外加两个参数,r表示行,c表示列。
我们可以写出如下方法。
遍历方向
public void dfs(int[][] grid, int r, int c) {
// 上
dfs(grid, r - 1, c);
// 下
dfs(grid, r + 1, c);
// 左
dfs(grid, r, c - 1);
// 右
dfs(grid, r, c + 1);
}
假设现在位于坐标(1,1)上,那么其上下左右分别就是(0,1)、(2,1)、(1,0)、(1,2)

接下来,我们就要考虑边界问题,首先就是网格的边界值,其实也就是行和列的边界值。
确定边界
public void dfs(int[][] grid, int r, int c) {
// 网格的边界值
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return;
}
// 上
dfs(grid, r - 1, c);
// 下
dfs(grid, r + 1, c);
// 左
dfs(grid, r, c - 1);
// 右
dfs(grid, r, c + 1);
}
当处理完边界值之后,我们就要考虑遍历到水域的问题了,很明显,当遍历到水域时,也就可以停止了。
public void dfs(int[][] grid, int r, int c) {
// 网格的边界值
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return;
}
// 当遍历到水域时,就应当停止了
if (grid[r][c] == 0) {
return;
}
// 上
dfs(grid, r - 1, c);
// 下
dfs(grid, r + 1, c);
// 左
dfs(grid, r, c - 1);
// 右
dfs(grid, r, c + 1);
}
重复遍历问题处理
到此,我们已经确定了深度优先遍历的边界条件,现在我们要考虑一下实际场景的问题,按照我们现在的边界停止条件,忽略了如下的场景:
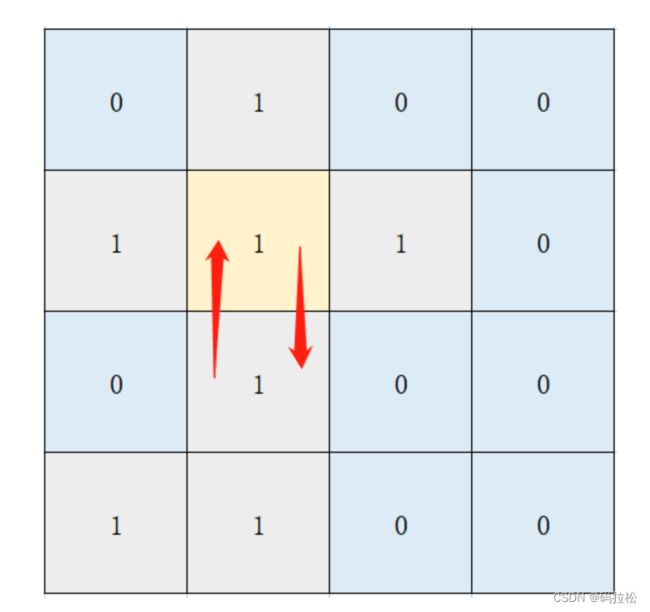
就是说,坐标(1,1)和(2,1)会互相作用,导致永远搜索不完,所以针对这种情况,我们还需要进行额外的处理,处理方式也很简单,一般情况下我们只需要记录一下每次走过的位置即可,当然方式有很多,比如放到Set集合,岛屿问题可以简单点处理,直接改变原有的值即可,比如直接将1改为2。
那么现在坐标(1,1)的值为2,然后要走到(2,1)。
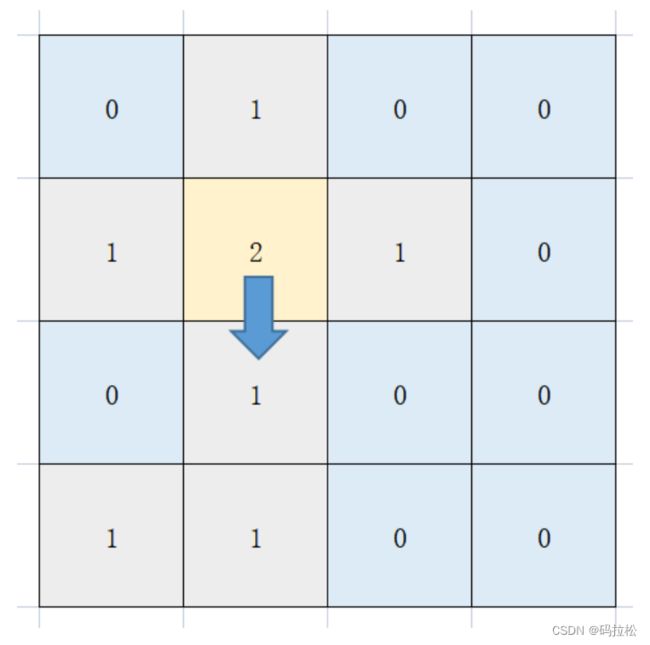
走到(2,1)后,我们也把值改为2,此时又从坐标(2,1)开始遍历,当向上遍历到(1,1)时就会直接停止了,因为此时(1,1)的值已经被改为2,即表示遍历过了。

到此为止,我们就算完成了一个标准的深度遍历模板了,现在可以用它来解题了!
模板解第一题
我们回到求岛屿的周长的问题,可以发现,所要找的岛屿的边,可以分为两种情况,一种是当遍历到网格边界时,其边界就是一条边,第二种情况就是,当遍历到水域时,也会有一条边。
代码如下
public int islandPerimeter(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 当遇到水域时,开始进行遍历
if (grid[i][j] == 1) {
return dfs(grid, i, j);
}
}
}
return 0;
}
public int dfs(int[][] grid, int r, int c) {
// 走向边界,周长加1
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return 1;
}
// 走向水域,周长加1
if (grid[r][c] == 0) {
return 1;
}
// 遍历过了,周长不变,直接返回
if (grid[r][c] == 2) {
return 0;
}
// 遍历过的陆地,设置为2,以免重复遍历
grid[r][c] = 2;
// 最后累加所有遍历结果
return dfs(grid, r - 1, c)
+ dfs(grid, r + 1, c)
+ dfs(grid, r, c - 1)
+ dfs(grid, r, c + 1);
}
第二题:求岛屿数量
这题基本上就是直接套用模板即可完成。
public int numIslands(char[][] grid) {
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 每次遇到陆地就加1,因为一旦遇到陆地,dfs就会一次性把联通的陆地全部改为2
if (grid[i][j] == '1') {
ans++;
dfs(grid, i, j);
}
}
}
return ans;
}
private void dfs(char[][] grid, int r, int c) {
// 网格的边界值
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return;
}
// 当遍历到水域时,就应当停止了
// 遍历过的也可以停止了
if (grid[r][c] == '0' || grid[r][c] == '2') {
return;
}
// 改为2,表示遍历过了
grid[r][c] = '2';
// 上
dfs(grid, r - 1, c);
// 下
dfs(grid, r + 1, c);
// 左
dfs(grid, r, c - 1);
// 右
dfs(grid, r, c + 1);
}
第三题:岛屿的最大面积

这题实际上就是遍历出所有岛屿,然后比较每个岛屿的大小,岛屿的大小也很容易得到。
在原有模板的基础上只需要稍微变动一下,即每次能走到陆地时加1即可,这样就能统计出每一片岛屿的大小。
代码如下
public int maxAreaOfIsland(int[][] grid) {
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
ans = Math.max(ans, dfs(grid, i, j));
}
}
}
return ans;
}
public int dfs(int[][] grid, int r, int c) {
// 走向边界,面积不变
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return 0;
}
// 走向水域,或者走过的陆地时,面积不变
if (grid[r][c] == 0 || grid[r][c] == 2) {
return 0;
}
grid[r][c] = 2;
// 累积当前遍历到的岛屿面积
return 1 + dfs(grid, r - 1, c)
+ dfs(grid, r + 1, c)
+ dfs(grid, r, c - 1)
+ dfs(grid, r, c + 1);
}
第四题:统计子岛屿

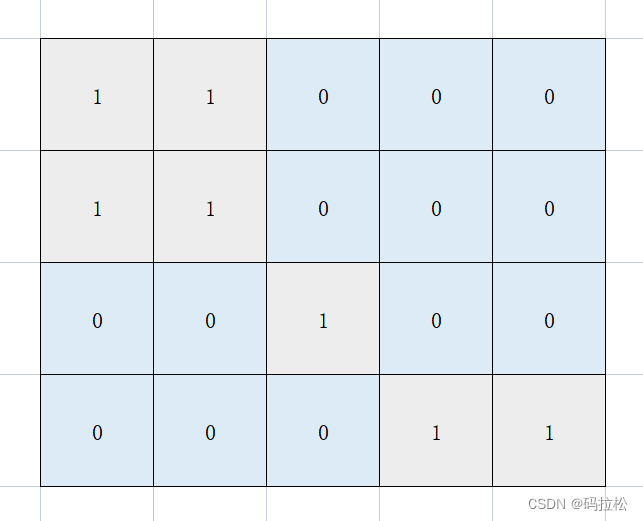
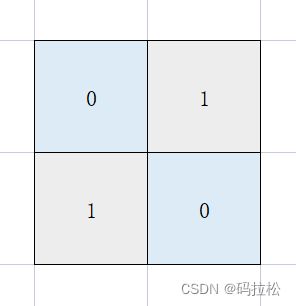
求子岛屿的意思,可以看作就是,求grid2是陆地,且在grid1也是陆地的部分,根据题目中的示例1所示结果:

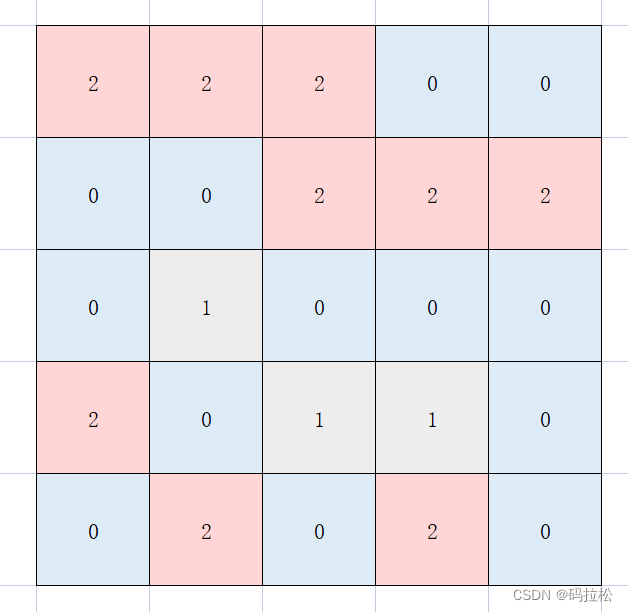
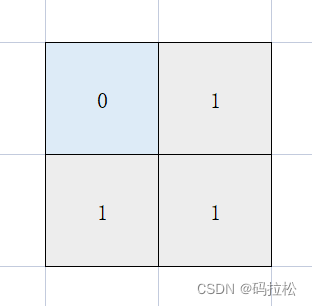
为了区分出红色1的部分,我们必须给出额外的标记,比如我们可以把1改为2,变成下图这样:
此时的网格与我们之前遇到的都不太一样,因为他出现了3种情况,即0,1,2,不过也不会很麻烦,我们只要认为现在0,1都是水域即可。
因此我们套用模板,代码如下:
public int countSubIslands(int[][] grid1, int[][] grid2) {
int ans = 0;
// 找到grid1和grid2重叠的部分,将grid2重叠的部分加1,直接用grid2[i][j] += grid1[i][j],即可完成。
for (int i = 0; i < grid2.length; i++) {
for (int j = 0; j < grid2[0].length; j++) {
if (grid2[i][j] == 1) {
grid2[i][j] += grid1[i][j];
}
}
}
// 此时,grid2,出现了3种情况,即0,1,2,我们可以认为0和1都不是陆地
for (int i = 0; i < grid2.length; i++) {
for (int j = 0; j < grid2[0].length; j++) {
if (grid2[i][j] == 2) {
ans++;
dfs(grid2, i, j);
}
}
}
return ans;
}
public void dfs(int[][] grid, int r, int c) {
// 网格的边界值
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return;
}
// 此时遍历到0和1,就应当停止了
// 3表示遍历过的,也可以停止了
if (grid[r][c] == 0 || grid[r][c] == 1 || grid[r][c] == 3) {
return;
}
// 改为3,表示遍历过了
grid[r][c] = 3;
// 上
dfs(grid, r - 1, c);
// 下
dfs(grid, r + 1, c);
// 左
dfs(grid, r, c - 1);
// 右
dfs(grid, r, c + 1);
}
如果,按照上述代码去执行,你会发现结果会多出一个岛屿来。
所以,我们还得额外处理一下2与1联通的情况,这种情况下是不能算做是子岛屿的,所以我们就还是需要将1和2一起来遍历,只不过遍历到1时要额外记录一下。
此时求解的问题可以转换为:遍历每一块岛屿,且每一块岛屿都由2组成。
最终代码实现
public int countSubIslands(int[][] grid1, int[][] grid2) {
int ans = 0;
// 找到grid1和grid2重叠的部分,将grid2重叠的部分加1,直接用grid2[i][j] += grid1[i][j],即可完成。
for (int i = 0; i < grid2.length; i++) {
for (int j = 0; j < grid2[0].length; j++) {
if (grid2[i][j] == 1) {
grid2[i][j] += grid1[i][j];
}
}
}
// 此时,grid2,出现了3种情况,即0,1,2,我们可以认为0和1都不是陆地,但遇到1需要额外记录,由于只有两种情况,遇到或没遇到,因此我们可以直接用boolean来代替
for (int i = 0; i < grid2.length; i++) {
for (int j = 0; j < grid2[0].length; j++) {
if (grid2[i][j] == 2) {
// dfs结果为true,表示没有遇到1
if (dfs(grid2, i, j)) {
ans++;
}
}
}
}
return ans;
}
public boolean dfs(int[][] grid, int r, int c) {
// 网格的边界值
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return true;
}
// 当遍历遇到1时,记录为false
if (grid[r][c] == 1) {
return false;
}
// 其他情况,都返回true
if (grid[r][c] == 0 || grid[r][c] == 3) {
return true;
}
// 改为3,表示遍历过了
grid[r][c] = 3;
// 注意这里要使用单&来处理,因为要走完每一条路,不然会出现漏改为3的情况
return // 上
dfs(grid, r - 1, c) &
// 下
dfs(grid, r + 1, c) &
// 左
dfs(grid, r, c - 1) &
// 右
dfs(grid, r, c + 1);
}
第五题:统计封闭岛屿的数目
封闭岛屿的定义,可以理解为:它是一个不在边界值上的岛屿,即满足岛屿的同时也满足0不会在落在网格的4条边上,有了这个条件之后,我们就好处理了,和第四题一样,还是可以用boolean值来做一个遍历到边界的额外记录。
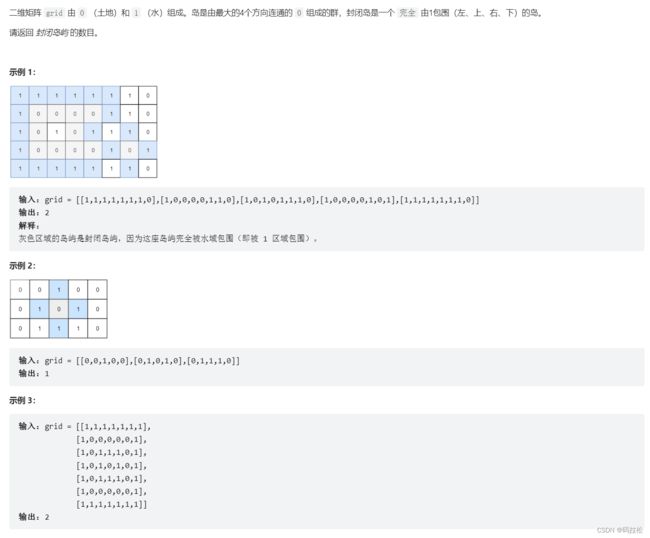
吐槽一下出题者,不按套路出牌,0是陆地,1是水域,这和前面的几题的定义是反过来的。。。
本题的模板,在判断边界条件时稍有改动,当走到边界时可以直接完成判断,和前面对比,也就少了一步标记为走过的,以及继续顺着走下去的情况。
之所以可以这样,是因为在所有的边界上,只要有一个不满足条件,那么就不满足封闭岛屿的要求。
比如,像下图这样,当从坐标(1,2),走向坐标(0,2)后,对于之前的题目,我们是需要从(0,2)开始继续向上下左右四个方向遍历的,但对于本题,就不需要了,因为一旦判断出(0,2)值为0,就可以确定这片为非封闭岛屿了。
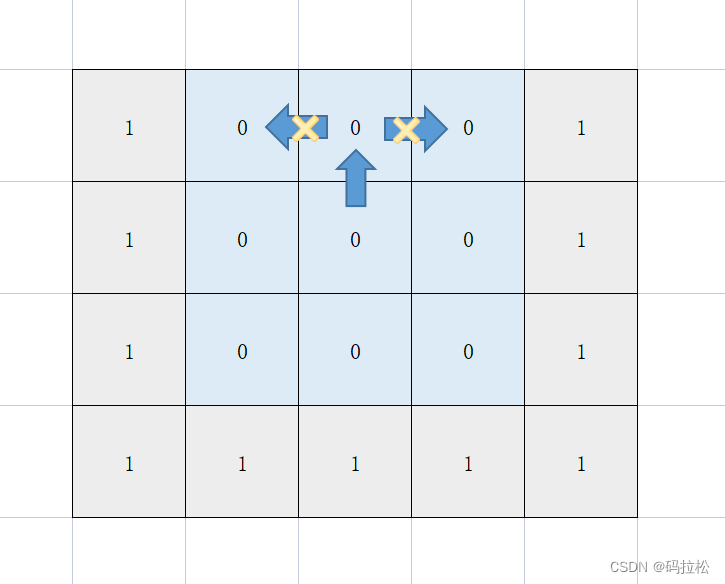
套用模板后,代码如下:
public int closedIsland(int[][] grid) {
int ans = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 注意本题0是陆地,1是水域。。。
if (grid[i][j] == 0 && dfs(grid, i, j)) {
ans++;
}
}
}
return ans;
}
public boolean dfs(int[][] grid, int r, int c) {
// 遇到网格的边界值时,判断是不是水域,只有是水域时才满足封闭岛屿的要求,
// 如果是陆地,不满足封闭岛屿的要求,因此可以不用继续顺着走下去了。
// 如果是水域,不满足岛屿的要求,因此也不用继续顺着走下去了。
if (r == 0 || c == 0 || r == grid.length - 1 || c == grid[0].length - 1) {
return grid[r][c] == 1;
}
// 当遍历到水域时,就应当停止了
// 遍历过的也可以停止了
if (grid[r][c] == 1 || grid[r][c] == 2) {
return true;
}
// 改为2,表示遍历过了
grid[r][c] = 2;
return
// 上
dfs(grid, r - 1, c) &
// 下
dfs(grid, r + 1, c) &
// 左
dfs(grid, r, c - 1) &
// 右
dfs(grid, r, c + 1);
}
第六题:最大人工岛
本题的思路,我们可以先计算每一片岛屿的面积,然后找到只隔一块水域的两个岛屿,相加其面积即可得到结果。
步骤分解:
1. 计算每一片岛屿的面积
这个好实现,就是前面第三题的方式。
2. 找到只隔一块水域的两个岛屿
当我们找到岛屿之后,就可以遍历所有水域,然后搜索每一块水域的上下左右,看看是不是岛屿,如果是岛屿就加上岛屿的面积。
因为要求水域的上下左右是不是岛屿,因此我们在计算每一片岛屿的面积的时候,可以顺带记录下每一片岛屿中陆地的坐标,这样即可根据坐标判断其是不是岛屿。
如下图,坐标{1,1}上下左右都是岛屿,并且每一片岛屿的面积都为1,因此最终面积为5,
其余坐标{0,0},{0,2},{2,0},{2,2}上下左右遍历后,最终面积都为3。
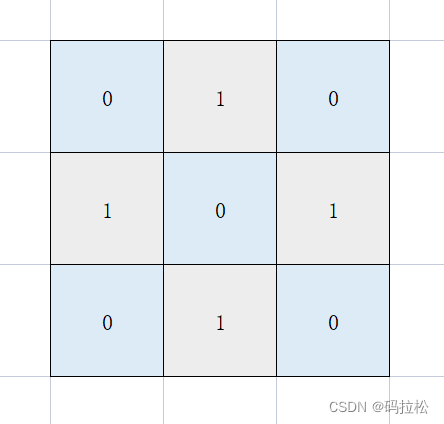
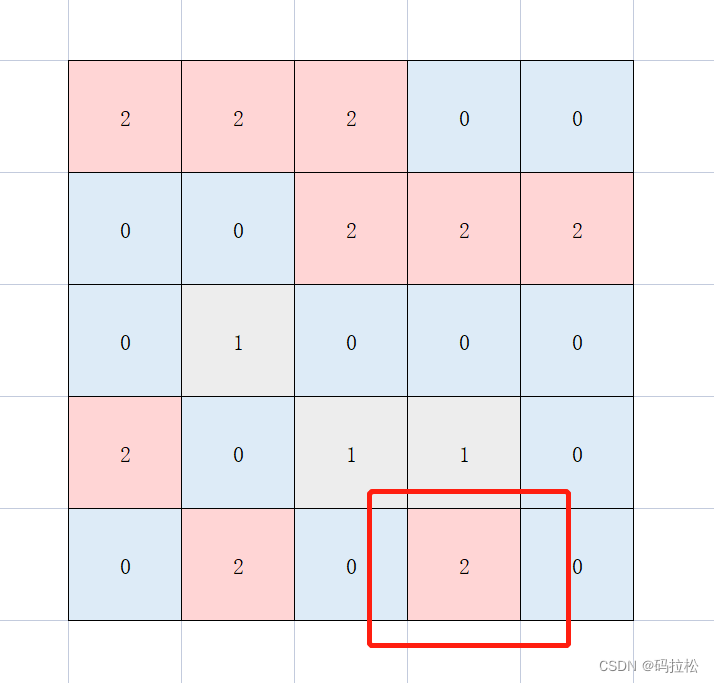
上述分析中,我们忽略了一种场景,如下图:
现在坐标{1,1}的上、左,和下、右,虽然都是岛屿,但上、左和下、右实际分别都是同一个岛屿,如果不处理的话,就会出现重复累加面积的情况,向上遍历时,发现岛屿面积为3,向左遍历时,也发现岛屿面积为3,最终会加两次3,导致结果错误。
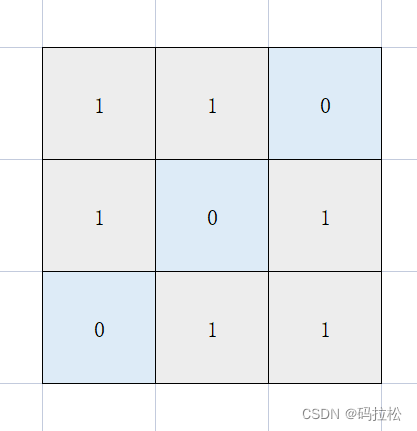
因此针对这种情况,我们就需要标记出每一个陆地的归属岛屿,这样当我们从水域开始进行上下左右遍历到陆地时,再判断陆地是不是归属于同一个岛屿即可避免重复计算的问题。
为了方便满足上述场景,我们可以使用一个Map来记录,Key直接记录为坐标,Value记录坐标对应的岛屿,以及岛屿的面积。
最终代码实现如下:
public int largestIsland(int[][] grid) {
int ans = 0;
// key为坐标,value为坐标对应的岛屿信息,包含:岛屿编号、岛屿面积
Map<String, IslandInfo> islandMap = new HashMap<>();
// 岛屿编号
int id = 1;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
int area;
IslandInfo islandInfo = new IslandInfo();
// 使用求岛屿面积的方式,只是多传了两个参数,用于处理islandMap信息
area = dfs(grid, i, j, islandMap, islandInfo);
// 设置岛屿编号和面积
islandInfo.id = id++;
islandInfo.area = area;
// 针对全岛屿情况,特殊处理
ans = Math.max(ans, area);
}
}
}
// 下面开始针对水域做处理,只要遍历每个水域的上下左右,如果发现是岛屿,并且岛屿编号不相同,即可加上岛屿面积。
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 0) {
// 找到上下左右
String up = search(grid, i - 1, j);
String down = search(grid, i + 1, j);
String left = search(grid, i, j - 1);
String right = search(grid, i, j + 1);
// 如果上下左右是岛屿,就从islandMap中取得岛屿信息
IslandInfo upIsland = new IslandInfo();
if (up != null) {
upIsland = islandMap.get(up);
}
IslandInfo downIsland = new IslandInfo();
if (down != null) {
downIsland = islandMap.get(down);
}
IslandInfo leftIsland = new IslandInfo();
if (left != null) {
leftIsland = islandMap.get(left);
}
IslandInfo rightIsland = new IslandInfo();
if (right != null) {
rightIsland = islandMap.get(right);
}
// 确认相邻岛屿非同一个岛屿后,即可累加相邻岛屿面积
int area = upIsland.area;
if (upIsland.id != downIsland.id) {
area += downIsland.area;
}
if (upIsland.id != leftIsland.id && leftIsland.id != downIsland.id) {
area += leftIsland.area;
}
if (upIsland.id != rightIsland.id && rightIsland.id != downIsland.id && rightIsland.id != leftIsland.id) {
area += rightIsland.area;
}
ans = Math.max(ans, area + 1);
}
}
}
return ans;
}
/**
* 非陆地返回:null
* 陆地返回:陆地坐标
*/
public String search(int[][] grid, int r, int c) {
// 边界非陆地
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return null;
}
// 返回陆地坐标
if (grid[r][c] == 2) {
return r + "," + c;
}
return null;
}
/**
* 通用模板,在计算岛屿面积的基础上,通过islandMap记录每一块陆地的坐标
*/
public int dfs(int[][] grid, int r, int c, Map<String, IslandInfo> islandMap, IslandInfo islandInfo) {
if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) {
return 0;
}
if (grid[r][c] == 0 || grid[r][c] == 2) {
return 0;
}
grid[r][c] = 2;
islandMap.put(r + "," + c, islandInfo);
return 1 + dfs(grid, r - 1, c, islandMap, islandInfo) +
dfs(grid, r + 1, c, islandMap, islandInfo) +
dfs(grid, r, c - 1, islandMap, islandInfo) +
dfs(grid, r, c + 1, islandMap, islandInfo);
}
/**
* 岛屿信息
*/
class IslandInfo {
// 默认编号为0
int id;
// 默认面积为0
int area;
}
总结
通过上面6题,应该可以体会出通用解决模板的套路,无论题目如何变化,其边界判断、水域、陆地判断、上下左右遍历都是非常标准的解决岛屿问题的方式,只要掌握了这个套路,其他无非就是在其基础上演化处理而已。