Unity ——使用贝塞尔曲线对三维管状物体进行弯曲

参考链接：【Unity】弹性鱼竿简单实现-通过贝塞尔曲线修改Mesh - 简书

参考论文：吴晓亮, 黄襄念. Unity 中使用贝塞尔曲线对三维物体进行弯曲[J]. 现代计算机, 2016 (5): 57-59.

unity项目下载：https://download.csdn.net/download/weixin_43042683/87690343

效果图

0 引言

随着虚拟现实的发展，在游戏引擎中对三维物体进行弯曲效果的模拟越来越重要。 在三维游戏引擎中，需要对一些三维的物体进行弯曲，以达到游戏操作中实时模拟物体弯曲。说到弯曲，自然而然想到曲线，从曲线的角度出发，那么关键就是如何生成曲线，以及如何根据曲线修改物体形状，从而达到弯曲的效果。 生成曲线的话，可以直接想到用贝塞尔曲线，传统的贝塞尔曲线算法被用 于各类图形制作软件中，如 Photoshop 等软件，但多限于二维线条的应用，在三维物体上的应用较少。 通过贝塞尔曲线算法结合三维物体的网格顶点，可以实现对条形三维物体进行弯曲变化。

1 贝塞尔曲线

Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。 1962年，法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名，称为贝塞尔曲线。

参考链接：Unity 贝塞尔曲线（Beizer curve）的原理与运用

1.1 一阶贝塞尔曲线

标准公式：

 示意图：

代码实现：

    // 一阶贝塞尔曲线，参数P0、P1、t对应上方原理内的一阶曲线参数.
    Vector3 Bezier(Vector3 p0, Vector3 p1, float t)
    {
        return (1 - t) * p0 + t * p1;
    }

1.2二阶贝塞尔曲线

标准公式：

示意图：

代码实现：

    // 二阶贝塞尔曲线，参数对应上方原理内的二阶曲线参数.
    Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, float t)
    {
        Vector3 p0p1 = (1 - t) * p0 + t * p1;
        Vector3 p1p2 = (1 - t) * p1 + t * p2;
        Vector3 temp = (1 - t) * p0p1 + t * p1p2;
        return temp;
    }

1.3三阶贝塞尔曲线

标准公式：

示意图：

   // 三阶贝塞尔曲线，参数对应上方原理内的三阶曲线参数.
    Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
    {
        Vector3 temp;
        Vector3 p0p1 = (1 - t) * p0 + t * p1;
        Vector3 p1p2 = (1 - t) * p1 + t * p2;
        Vector3 p2p3 = (1 - t) * p2 + t * p3;
        Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
        Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
        temp = (1 - t) * p0p1p2 + t * p1p2p3;
        return temp;
    }

1.4 n 阶贝塞尔曲线

标准公式：

代码实现：

//贝塞尔曲线公式
private Vector3 CalculateBezier(float t)
{
    Vector3 ret = new Vector3(0, 0, 0);
    int n = 阶数;
    for(int i = 0; i <= n; i++)
    {
        Vector3 pi = 第i个控制点的坐标;
        ret = ret + Mathf.Pow(1 - t, n - i) * Mathf.Pow(t, i) * Cn_m(n, i) * pi;
    }
    return ret;
}
//组合数方程
private int Cn_m(int n, int m)
{
    int ret = 1;
    for(int i = 0; i < m; i++){
        ret = ret * (n - i) / (i + 1);  
    }
    return ret;    
}

设计思路

在三维物体上添加多个控制点，其中控制点可以使用n个空节点来代替，控制点的坐标即为空节点的坐标。至于t值，可以看作顶点到底部的距离与整个三维物体长度的比值，0<= t <=1。这样设计的话，我们第一个控制点P0应该在三维物体的底部位置，而最后一个控制点Pn应该在三维物体的顶部位置。

2.弯曲的实现 

根据上面公式计算出的只是一条曲线，而我们的目的是三维物体模型能按照这个曲线进行弯曲。

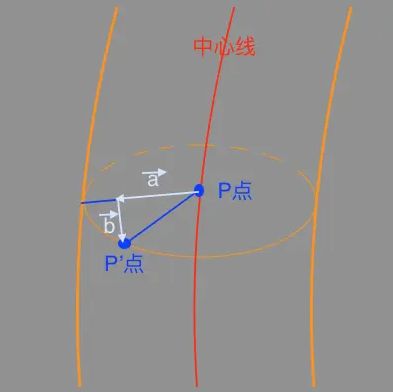
对于管状物体来说，我们计算出来的曲线其实是它的中心线，而mesh顶点应该位于中心线的两侧，所以顶点弯曲后的坐标是应该要由贝塞尔曲线计算的坐标经过一定变换得来。
经过观察可以发现，弯曲后顶点的坐标P'应由计算出的曲线上的坐标P进行两次偏移得出：在该点法线方向上进行偏移a、在垂直于弯曲面的方向上进行偏移b。

 对应代码如下：

// 对原来的顶点做贝塞尔曲线变换，得到弯曲变换后对应的点位置
private void UpdateBezierBend()
{   
    oriVertices = 模型未弯曲时的顶点数组;
    topPos = 最后一个控制点的坐标，用来计算模型长度;
    bendVector = 弯曲方向;
    for(int i = 0; i < oriVertices.Length; i++)
    {
        //获取顶点坐标,计算t值
        Vector3 oriPos = oriVertices[i];
        float t = oriPos.y / topPos.y;
        //获取顶点在贝塞尔曲线上对应的坐标
        Vector3 p = CalculateBezier(t); 
        //获取顶点在曲线上应有的法线偏移向量
        Vector3 vectorA = GetBendNormalVector(t, oriPos, bendVector); 
        //获取顶点在曲线上应有的垂直偏移向量
        Vector3 vectorB = new Vector3(oriPos.x, 0, oriPos.z) - Vector3.Project(new Vector3(oriPos.x, 0, oriPos.z), bendVector); 
        //获取顶点最终弯曲位置
        vector3 p' = p + vectorA + vectorB;
    }
    todo-修改顶点坐标;
}
// 获取指定点上的法向量偏移
private Vector3 GetBendNormalVector(float t, Vector3 oriPos, Vector3 bendVector)
{
    Vector3 tangentVector = CalculateBezierTangent(t);//切线斜率
    Vector3 normalVector = 由法线和切线互相垂直计算出法线方向；
    //法线向量的模应为到投影到弯曲面后，到中心点的距离
    float magnitude = Vector3.Project(new Vector3(oriPos.x, 0, oriPos.z), bendVector).magnitude;
    normalVector = normalVector.normalized * magnitude;
    return normalVector;
}
//对曲线公式求导得出切线向量
private Vector3 CalculateBezierTangent(float t)
{
    Vector3 ret = new Vector3(0, 0, 0);
    int n = 阶数;
    for(int i = 0; i <= n; i++)
    {
        Vector3 pi = 第i个控制点的坐标;
        ret = ret + (-1 * (n - i) * Mathf.Pow(1 - t, n - i - 1) * Mathf.Pow(t, i) * Cn_m(n, i) * pi + i * Mathf.Pow(1 - t, n - i) * Mathf.Pow(t, i - 1) * Cn_m(n, i) * pi);
    }
    return ret;
}

这样我们就实现了通过控制点生成曲线，通过曲线弯曲物体的方法。

3.构造受力模型

简单构造一个受力模型，通过物体施加拉力，拉力使控制点发生变化，从而使物体弯曲。设定一个Cube为施加拉力F的物体，然后为每个控制点设定一个完全弯曲所需要的力Fc，然后设定控制点朝拉力方向弯曲的角度为：
a = Mathf.Clamp(F/Fc, 0, 1.0) * 拉力与控制点的夹角;
为了模拟比较真实的弯曲效果，Fc可以看成三维物体每小节的的弹力大小，越靠近底部的控制点Fc就越大，越难弯曲，反之，越靠近顶部的控制点Fc越小，也就越容易弯曲。
代码如下：

private void UpdateControlPoint()
{
    float F = Cube.force;
    //根据受力计算各个控制点旋转角度
    n = 控制点数量;
    for(int i = 1; i < n - 1; i++)//第一个和最后一个点不计算弯曲
    {
        //计算最大弯曲方向
        Vector3 toVector = 施力物体相对控制点pi的方向;
        Quaternion maxRotation =  Quaternion.FromToRotation(Vector3.up, toVector);
        //计算弯曲比例
        float rotateRate = Mathf.Clamp(F / Fc, 0f, 1.0f);
        //设置旋转角度
        pi.localRotation = Quaternion.Lerp(Quaternion.Euler(0, 0, 0), maxRotation, rotateRate);
    }
}

4. 结语

该方法做出来的弯曲效果还是很自然的（如效果图），使用也比较简单，且不需要关节控制。但是比较吃性能，另外考虑到光照，顶点坐标更新后需要重新计算下mesh的法线信息normals。 

目前该方法对于管状的三维物体效果较佳，对于形状复杂的三维物体效果很差。该方法要求三维物体的顶点数要尽量多才能有效果。顶点数少的话很容易造成三维物体的扭曲变形。