前缀和算法【一维、二维】

算法推导

首先这种算法适合于求从 x 到 y 的和。

一维情况

一维代码十分简单，我们只需要每个都记录前面所有的和即可，注意细节 下标从1开始

for(int i = 1 ; i <= n ; i ++){
	cin >> temp;
	a[i] = a[i - 1] + temp;
}

这里我们就看两种情况：一种是 开始时 ，一种是 执行中

在开始时，因为我们是从1开始，a[0] = 0，所以第一个就是temp;

在执行过程中，因为前一个是前面所有的数字之和，加上temp就变成当前数字之和了

二维情况

二维的前缀和则分为两个部分，一个是计算前缀和，另一个则是计算从（x1,y1）到（x2,y2）的值

计算前缀和

假设我们输入的值为

1	1	1	1
1	1	1	1
1	1	1	1

现在我们需要处理的前缀和

	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4
3	0	3
4	0	4

问题一：如何计算前缀和数组的元素？

若我们需要计算a[i][j]，我们需要计算a[i-1][j] + a[i] [j-1] + temp - a[i-1][j-1]。

上面元素 + 左边元素 - 左上角元素

• a[i-1][j]：表示前面 列的前缀和
• a[i] [j-1]：表示前面的 行的前缀和

所以两个直接相加 ，再加上temp，就能得到此单元格的内容

但是需要注意的是，前面两个会将a[i-1][j-1]都加进去，所以这里需要 减去一个 即可

现在我们计算a[1] [1] = a[0][1] + a[1][0] + a[0][1] - a[0][0] + 1 = 1

计算行

a[2] [1] = a[1][1] + a[2][0] + 1 - a[1][0] = 2

计算列

a[1][2] = a[1][1] + a[0][2] + 1 - a[0][1] = 2

a[2][2] = a[2][1] + a[1][2] - a[1][1] + 1 = 2 + 2 - 1 +1= 4

	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4
3	0	3
4	0	4

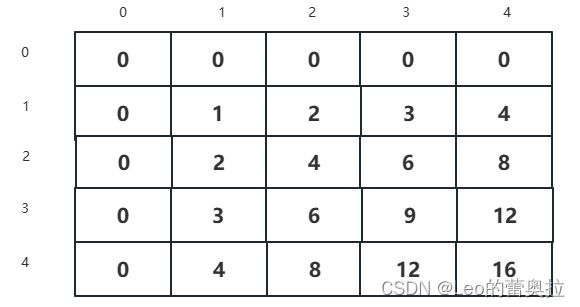
同样的处理后我们将得到以下表格

	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
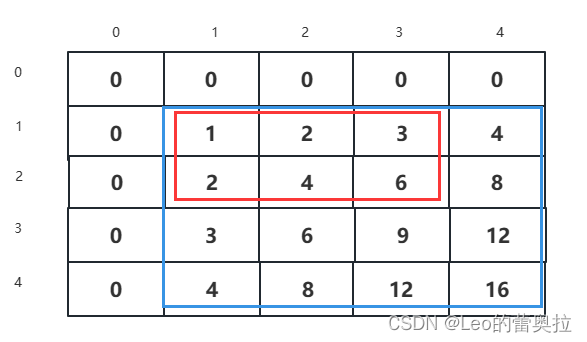
2	0	2	4	6	8
3	0	3	6	9	12
4	0	4	8	12	16

得到代码

for(int i = 1 ; i <= n ; i ++){
	for(int j = 1 ; j <= m ; j ++){
		cin >>temp ;

		a[i][j] = a[i - 1][j] + a[i][j - 1] + temp - a[i-1][j-1];
	}
}

计算结果

现在假设我们需要计算（x1,y1）和（x2,y2）的和。

因为前面我们已经获得了前缀和的一个数组，但是都是基于（1，1）这个点，现在需要改变起点，就需要进行重新计算

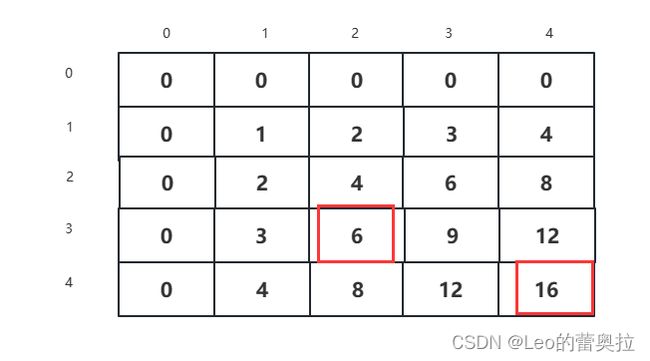
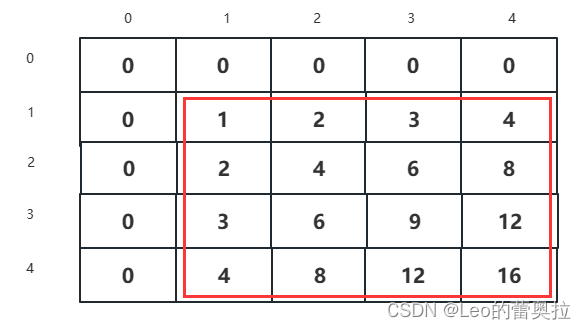
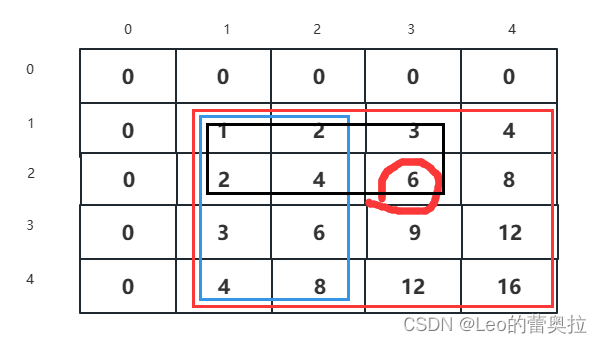
假设当前我们需要计算（2,3）到（4,4）

首先我们需要明确这两个位置表示的数字意思

• (2,3)：表示从（1,1）开始到（2,3）的前缀和

  

• （4,4）：表示从（1,1）开始到（4,4）的前缀和）

  

从两个图中，很容易发现这两者有相交的地方

所以，我们需要进行相减

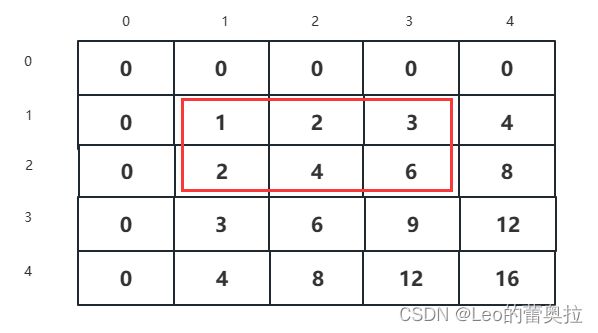
我们需要减去这两个内容（蓝色框 + 黑色框）

对应到数组内分别对应

• 蓝色：a[x1 - 1][y2]
• 黑色：a[x2][y1-1]

但是很明显的，这中间同样也减了两次相同的内容：a [x1 - 1] [ y1 - 1]，所以需要加上

解决代码

while(q--){
	cin >> x1 >> y1 >> x2 >> y2;

	cout << a[x2][y2] - a[x1 - 1][y2] - a[x2][y1 - 1] + a[x1 - 1][y1 - 1];
}

完整代码

一维

#include 

using namespace std;

const int N = 100009;

int a[N];

int main()
{
    int n , m , temp = 0;

    cin >> n >> m;

    for(int i = 1 ; i <= n ; i ++){
        cin >> temp;
        a[i] = a[i - 1] + temp;
    }

    int l , r ;
    while(m--){
        cin >> l >> r;
        cout << a[r] - a[l - 1] << endl;
    }

    return 0;
}

二维

#include

using namespace std;

const int N = 1008;

int a[N][N];
int n ,  m , q;


int main(){
    cin >> n >> m >> q;
    int temp;
    for(int i = 1 ; i <= n ; i ++){
        for(int j = 1 ; j <= m ; j ++){
            cin >> temp;
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] +temp;
        }
    }
  
    int x1 , y1 , x2 , y2;
    while(q --){
        cin >> x1 >> y1 >> x2 >> y2;
      
        cout << a[x2][y2] -a[x1-1][y2] - a[x2][y1 - 1] + a[x1-1][y1-1] << endl; 
      
    }
  
    return 0;
}