来自清华的AdaSP：基于自适应稀疏成对损失的目标重识别

摘要

论文链接：https://arxiv.org/abs/2303.18247
物体重识别(ReID)旨在从大型图库中找到与给定探针具有相同身份的实例。成对损失在训练强大的ReID网络中发挥着重要作用。现有的成对损失密集地利用每个实例作为锚，并在小批量中对其三元组进行采样。这种密集采样机制不可避免地引入了视觉相似性很少的正对，这可能对训练有害。为解决该问题，本文提出一种新的损失范式，称为稀疏成对损失(SP)损失，只利用小批量中每个类的少数适当对，并根据经验证明，它对ReID任务足够。基于所提出的损失框架，我们提出了一种自适应的正挖掘策略，可以动态适应多样化的类内变化。广泛的实验表明，SP损失及其自适应变体AdaSP损失优于其他成对损失，并在几个ReID基准上取得了最先进的性能。代码可以在https://github.com/Astaxanthin/AdaSP上找到。

1、简介

目标重识别(ReID)是视觉监控中最重要的视觉任务之一。它旨在将不同场景下不同摄像头捕获的相同身份的行人/车辆图像关联起来。最近，随着深度神经网络在计算机视觉领域的繁荣，ReID任务迅速发展到更复杂的特征提取器[8,37,40,44,60,61]和更复杂的损失[43,45,57,58]。在重识别任务[35]中，受益于量化两幅图像的语义相似度/距离，度量损失与身份损失被广泛应用以提高排序精度。

图1所示。密集成对损失和稀疏成对(SP)损失之间的区别。为简单起见，这里只显示了两个类，用圆圈和三角形标记。红色圆圈代表锚点。密集成对损失，如三元组损失[19]和循环损失[45]，将每个实例视为一个锚，并挖掘其正负对来构建一个损失项。SP损失将每个类别视为一个单元，并分别挖掘信息量最大的正对和负对，而不使用锚点。

通常，度量损失用于度量学习，其目的是将原始信号映射到低维嵌入空间，其中类内实例聚类，类间实例分离。成对框架，如三元组损失[19]和循环损失[45]，使用锚点来拉出它们的正对，同时将负对推开。大多数现有的成对损失[14,19,38,45]致力于利用小批量中的所有实例，并密集锚定每个实例(我们称之为密集成对方法)以对其三元组进行采样。尽管开发了一些困难的样本挖掘方法[7,45,50,51]以加速收敛或提高性能，但这些损失仍然以密集的方式计算(即图1中的顶部行)。这种密集设计不可避免地引入有害的正对[1,43]，它们具有很少的视觉相似性，并可能导致度量学习的优化[54]的糟糕局部最小值，因为由光照变化、遮挡、不同视角引起的大类内变化(图2a)等。

在这现工作中，没有必要在一个小批量中使用所有实例，因为它们中的大多数要么是微不足道的，要么是有害的对。本文提出一种新的损失范式，即稀疏成对损失(SP)损失，只利用小批量中每个类的信息量最大的对，而不依赖密集的实例级锚点，如图1(最底层)所示。对于对象ReID任务，根据经验发现，只要挖掘出适当的类别，只使用每个类别的几对就足以进行损失计算。基于提出的损失框架，我们对正向挖掘策略进行了严格的研究。

与已经被积极研究的负挖掘相比[14,42,54]，正挖掘仍未被充分开发。一般来说，一个合适的正对应该能够适应不同程度的类内变化。例如，在侧面视角或黑暗照明下被遮挡的行人与图2a中他的正面视角几乎没有视觉相似性，而在没有任何遮挡的清晰照明下的实例(蓝色边界框)可以桥接它们，从而形成适合训练的一对。为了获得适当的正对，一些工作[25,43,55]试图挖掘“中等”或容易的正对，但仍然依赖于密集的锚点。

图2。行人识别数据集中不同水平的类内变化。(a)密集遮挡、光照变化和视角不同导致的类内变化大。在这种情况下，挖掘构成最大类内超球半径的最硬正对对度量学习是有害的，而塑造最小超球半径的最硬正对则是合适的度量学习。(b)视觉特征高度相似的类内变化小。在这种情况下，最困难和最不困难的例子在视觉上都有明显的相似性。

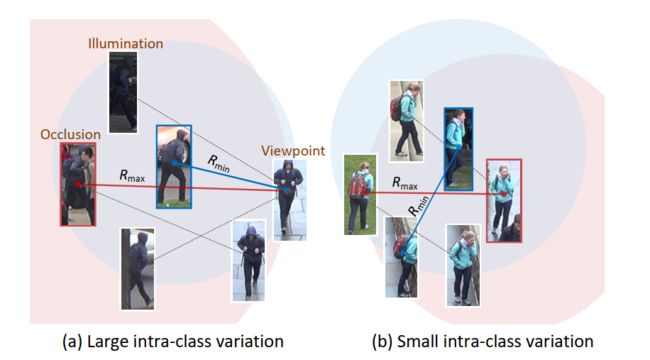
本文首先提出一种难度最小的正挖掘策略，以解决较大的类内变化。受几何见解的启发，一类中最硬的正对塑造了覆盖所有类内样本的最大超球体的半径。然而，由于类内差异很大，它可能会过大，从而引入压倒性的视觉差异。在这种情况下，构建最小超球的最不困难的正对可以被用作更合适的具有明显视觉相似性的正对(图2a)。此外，为了处理具有不同类内变化的类(图2)，开发了一种自适应挖掘方法，自动重加权这两类正对，根据类的特定情况塑造一个动态的类内超球。本文的主要贡献总结如下：

• 本文提出一种新的成对损失框架——稀疏成对损失——仅利用小批量中每个类的少量信息正/负对。
• 提出了一种难度最小的正挖掘策略，以解决较大的类内变化，并进一步赋予它一种根据每个小批量中不同级别的类内变化的自适应机制。
• 在各种人员/车辆ReID数据集上评估了所提出的AdaSP损失，并在不同基准上优于现有的密集成对损失。

2、相关工作

物体 ReID。物体重识别(Object ReID)，包括行人和车辆的再识别，被广泛应用于非重叠摄像头的智能监控系统中[4,20]。目前，特征表示学习和深度度量学习已经成为ReID任务的常规步骤，在早期研究中，它们取代了手工设计的特征[13,36]和距离度量学习[24,31,53]。为了缓解特征表示中的不对齐，许多研究[5,27,37,40,44,48,60,61]将局部聚合特征与全局表示相结合，在人/车重识别任务中取得了显著的改进。最近，视觉transformer[8,46]被引入到ReID研究中[18,26,40]，以获得更具判别力的特征表示。此外，Fu等[10,11]成功地在大规模无标签行人重识别数据集上进行了预训练，以提高泛化性能。

深度度量学习。度量学习主要关注设计一种度量损失，使其能够最大化嵌入空间中的内部相似性，同时最小化嵌入空间中的内部相似性。通过将每个实例视为一个锚，许多成对度量损失，如三元组损失[19]及其变体[5,12,57,58]、四元组损失[3]和提升结构损失[38]，要求锚正对的相似性高于锚负对的相似性。为了进一步增强硬样本的权重，多相似度损失函数[50]、排名损失函数[51]和循环损失函数[45]分别根据相对相似度和最优状态对每个损失函数进行加权。除了ReID和图像检索任务，Prannay等人[22]提出了一种监督对比损失来解决图像分类任务。然而，这些成对损失高度依赖于实例级锚点，并需要密集地挖掘每个锚点的正对。

难样本挖掘。为了缓解训练过程中琐碎三元组占主导地位的问题，硬样本挖掘在度量学习中起着至关重要的作用。Alexander等人[19]根据经验证明，在小批量中挖掘最难的正负对的三元组损失优于对所有三元组进行采样的三元组损失。然而，当锚点-正对的相似性远低于锚点-负对时，最困难的对可能会导致糟糕的局部最小值[38,42,54,56]，特别是对于较大的类内变化。这个问题的解决方案大致集中在挖掘“不那么难”的负面/正面因素上。例如，一方面，Florian等[42]利用相似度低于锚点正的半硬负对，而Ben等[14]和Bhavya等[47]挖掘智能硬负对和最优硬负对，以避免选择过于困难的硬负对;另一方面，Hailin等[43]选择适度的正例对来减少较大的类内变化的影响，而其他研究[25,55]直接对三元组的生成进行简单的正例挖掘。

3、方法

3.1、稀疏成对损失

给定一个由K个随机类组成的mini-batch，每个mini-batch包含N个实例，我们表示第i类中第N个实例的归一化嵌入向量为${\mathbf{z}}_n^i=\frac{{\mathbf{w}}_n^i}{\Vert {\mathbf{w}}_n^i\Vert }$。相应地，任意两个实例之间的度量可以用它们的点积相似度来描述。本文没有将每个实例视为锚，而是提出了稀疏成对损失(SP)，以分别挖掘每个类别的正对和负对。小批量的SP损失可以表示为:
$${\mathcal{L}}_{SP}=\frac{1}{K}\sum _i^K\log \left(1+e^{\frac{S_i^{-}-S_i^{+}}{\tau }}\right)\text{\hspace{1em}(1)}$$

其中$\tau$是一个温度参数。$S_i^{-}$表示第i类选择的负对与所有$(K-1)N\times N$个负对的相似度。本文挖掘了最困难的一个，因为它描述了类之间的最小距离，并代表了所有负对中信息量最大的一对。相应地，采用最硬负相似度的软版本:
S i − ≈ τ log ⁡ ( ∑ n = 1 N ∑ j = 1 , j ≠ i K ∑ m = 1 N e z n i z m j τ ) (2) S_{i}^{-} \approx \tau \log \left(\sum_{n=1}^{N} \sum_{j=1, j \neq i}^{K} \sum_{m=1}^{N} e^{\frac{z_{n}^{i} z_{m}^{j}}{\tau}}\right) \tag{2} Si−​≈τlog ​n=1∑N​j=1,j=i∑K​m=1∑N​eτzni​zmj​​ ​(2)
作为类比，$S_i^{+}$表示适当的正相似度，这将在3.2节和3.3节详细描述。从表面上看，SP损失要求每个类别的最难负相似度小于其适当的正相似度。虽然本质上，它将每个类视为一个单元，并以稀疏的方式最大化其类间和类内相似性之间的差异，这与其他成对方法不同，这些方法密集地生成每个对应于单个实例的损失项。

图3。SP损失和其他密集成对损失之间裕度差异的示意图。黑点和绿色三角形表示不同类别的样本。蓝色圆圈以锚点A为中心，半径为其正对AB。橙色虚线圆圈表示由外边距扩展的边界。(a)密集成对损失采用固定间隔。它们需要手动微调超参数，以扩大正对和负对之间的相似性/距离的差异。(b) SP损失的动态边际。稀疏地为每个类别而不是每个实例挖掘最难的负样本对，形成一个间隔，动态扩展类边界并将负样本推到外部。

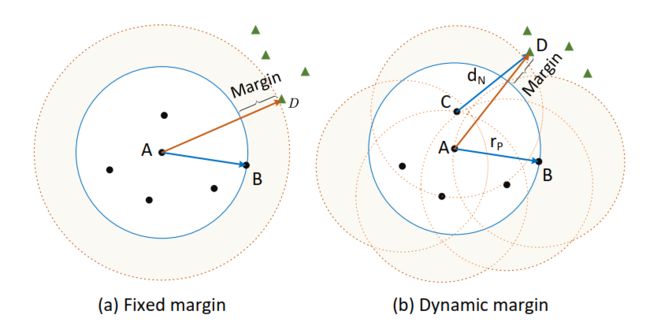
隐式动态边际。所提出的SP损失的另一个优点是，它不需要显式间隔作为超参数，这在许多密集的成对损失[19,45,50]中被广泛利用，以扩大正负之间的差异。相反，SP损失施加了一个隐含的动态裕度，如图3b所示。假设正对构成覆盖所有类内样本的超球$\left(h_P\right)$的半径，记为$r_P$，那么SP损失要求类间距离$d_N$大于类内半径。因此，根据不等式$r_P<d_N<d_{AD}$，即负样本，几何上被排除在半径为$r_P$的K个超球面并集所形成的动态边界之外。此后，如果我们像其他密集损失一样将$h_P$的中心作为一个锚点，由于$r_P<d_{AD}<2r_P$，其正负对之间的间隔从0到$r_P$ 而密集成对损失通常配置固定的预定义间隔，如图3a所示。

3.2、最小难度的正样本挖掘

通常，第i类中最难的正向对的相似度可以用软版本生成：
$$S_{i,h}^{+}\approx -\tau \log \left(\sum _{n=1}^N\sum _{m=1}^N{e}^{-\frac{{\mathbf{z}}_n^i{\mathbf{z}}_m^i}{\tau }}\right)\text{\hspace{1em}(3)}$$

从几何上讲，最难的正向对会形成以该正对的任意一个实例为中心的超球体半径，并覆盖该类内的所有其他实例，如图4a所示。类似地，每个实例与其最远的正样本配对后，可以形成不同半径的类内超球体。相应地，第n个正对的相似度可以由:
$$S_{i,n}^{+}\approx -\tau \log \left(\sum _{m=1}^N{e}^{-\frac{{\mathbf{z}}_n^i{z}_m^i}{\tau }}\right)\text{\hspace{1em}(4)}$$
因此，每个类可以得到N个不同大小的超球，其中最难的正向对所构造的超球是最大的超球(图4)。然而，复杂的光照、强烈的遮挡、不同的视点通常会造成较大的类内变化，这必然会导致正对视觉差异过大，尤其是最难的正向对。在这种情况下，在嵌入空间中夸大最难对的相似度将在很大程度上与原始数据特征相矛盾，从而误导特征学习。

图4。不同级别的类内变化示意图。黑点和绿色三角形表示不同类别的样本。最硬和最不硬的正对分别确定覆盖所有类内样本的最大超球(红色)和最小超球(蓝色)的半径。灰色圆形表示以其他实例为中心的超球体，半径不同，对应于最远的一对。SPL和SPS分别表示最大超球和最小超球的正相似度。(a)类内差异大。最大超球体和最小超球体的尺寸有显著差异。(b)类内变异小。在这种情况下，所有超球体都具有相似的大小。

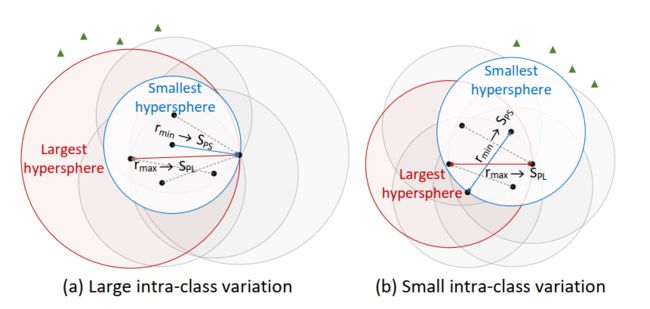
为了解决这个问题，我们软化了难挖掘策略，选择构造最小超球的最少难正向对(图4a)，最少硬正向对的相似度可以由:
S i , l h + ≈ τ log ⁡ ( ∑ n = 1 N e S i , n + τ ) = τ log ⁡ ( ∑ n = 1 N 1 ∑ m = 1 N e − z n i z m i τ ) (5) \begin{aligned} S_{i, l h}^{+} & \approx \tau \log \left(\sum_{n=1}^{N} e^{\frac{S_{i, n}^{+}}{\tau}}\right) \\ & =\tau \log \left(\sum_{n=1}^{N} \frac{1}{\sum_{m=1}^{N} e^{-\frac{z_{n}^{i} z_{m}^{i}}{\tau}}}\right) \end{aligned} \tag{5} Si,lh+​​≈τlog(n=1∑N​eτSi,n+​​)=τlog ​n=1∑N​∑m=1N​e−τzni​zmi​​1​ ​​(5)

值得注意的是，对于以最小超球为中心的实例，最不难的正向对仍然是难对，但它在整个类中产生的学习信号比最难的正向对弱，可以有效降低类内变化较大的影响。

糟糕的局部极值优化。在训练具有较大类内变化和较低类间变化的数据集时，密集成对损失会受到糟糕的局部最小值优化。因为在这种情况下，锚点图像很可能与最困难的负面图像更相似，而不是它的正面图像。我们认为他们是有害的三胞胎。因此，锚点在引入有害三元组方面起着重要作用。相反，由于无锚点设计和最少难度挖掘策略，SP损失可以很大程度上降低形成有害三元组的可能性。除了定量结果外，我们还提供了理论证明，证明SP在小批量中采样的有害阳性对的期望百分比低于密集采样方法，这在补充材料中显示。

因此，为了在鲁棒训练阶段衡量它们的差异，我们计算mini-batch中第i类最难和最容易相似度的调和平均值，如下所示:
$$h_i=\frac{2S_{i,lh}^{+}{S}_{i,h}^{+}}{S_{i,lh}^{+}+S_{i,h}^{+}}\text{\hspace{1em}(6)}$$

相应地，如果最难的正相似度与最难的正相似度之间存在较大差距，则调和平均值接近较小的正相似度，即最难的正相似度。而如果它们的相似度很接近，调和均值将接近它们的正态均值。调和均值随着最硬正相似度的增大而增大，这在很大程度上揭示了最硬正对的显著性。

因此，我们采用相似度的调和平均值(没有梯度反向传播)作为自适应权重，以平衡每个类别中最难和最难的正向对:

$${\alpha }_i=\{\begin{array}{ll}{h}_i& S_{i,h}^{+}⩾0\\ 0& S_{i,h}^{+}<0\end{array}\text{\hspace{1em}(7)}$$

利用上述正对的权重，加权正相似度可以得到：
$$S_i^{+}={\alpha }_i{S}_{i,h}^{+}+\left(1-{\alpha }_i\right)S_{i,lh}^{+}\text{\hspace{1em}(8)}$$

因此，公式1中的mini-batch的整个度量损失可以重写为:
$${\mathcal{L}}_{SP}=\frac{1}{K}\sum _i^K\log \left(1+e^{\frac{S_i^{-}-\left({\alpha }_i{S}_{i,h}^{+}+\left(1-{\alpha }_i\right)S_{i,lh}^{+}\right)}{\tau }}\right)\text{\hspace{1em}(9)}$$

从几何角度看，加权正相似度$S_i^{+}$表示一个半径可变的动态超球体，使损失函数能够自动适应不同程度的类内变化。

与现有方法的比较。密集的成对损失由锚正和锚负对产生。它们中的大多数[22,38,51]密集采样每个正例对，并挖掘困难的负例对，建立三元组用于度量学习。最近的一些研究集中在挖掘信息正对以加快训练收敛，如表1所示。三元组[19]和循环损失[45]利用了最硬的锚点正对。MS[50]和MP损失[43]根据最硬负向量对的相似度来选择锚点正向量对，以避免因类内变化过大而导致的局部极值。EP[55]损失直接采用最简单的锚-正对构造三元组。所提出的SP损失不依赖实例级锚点，而是挖掘每个类别的信息正对。SP-H和SP-LH旨在挖掘最难和最难的正例对。AdaSP根据类内变化程度动态改变正相似度。

4、实验

为了证明SP损失在对象ReID任务中的优势，我们首先在三个行人ReID数据集(Market- 1501 [62]， DukeMTMC-reID [41]， MSMT17[52])和两个车辆数据集(VeRi-776 [32]， VehicleID[33])上比较了单个SP损失与其他当前度量损失的性能，包括三重组损失[19]，多相似度(MS)损失[50]，圈损失[45]，监督对比(SupCon)损失[22]和容易正(EP)三重组损失[55]。其次，我们探讨了度量损失对增加类内变化的鲁棒性。然后，我们采用不同的网络架构来评估将所提出的AdaSP与身份丢失相结合所取得的ReID性能改善。此外，我们还研究了SP损失的超参数对ReID任务性能的影响。最后，我们在7个行人员/车辆基准上广泛评估了AdaSP损失，并将其与最先进的方法进行了比较。

数据集和评估指标。采用CUHK03[30]、Market-1501[62]、DukeMTMC-reID[41]、MSMT17[52]四个人ReID数据集和VeRi-776[32]、VehicleID[33]、VERI-WILD[34]三个车辆ReID数据集对我们的方法进行评估。每个数据集的详细信息汇总在Tab中。S1(补充材料)。我们采用了广泛采用的指标，包括平均平均精度(mAP)， Rank1 (CMC@1)和Rank5 (CMC@5)来量化ReID结果。

实现细节。对于行人ReID任务，我们采用了流行的MGN[48]与实例批处理规范化(IBN)[39]在Fast-ReID[17]中作为骨干，除非有特殊说明。嵌入特征的大小设置为256。在不同的实验中，输入图像大小设置为384 × 128或256 × 128。对于车辆ReID任务，我们采用ResNet-50 [16]， IBN为骨干。嵌入特征的大小设置为2048。所有实验的输入图像大小设置为256×256。对于这两个任务，总体损失由恒等损失(即交叉熵损失)和度量损失(我们的方法中的SP损失)组成:
$$\mathcal{L}={\mathcal{L}}_{ID}+\lambda {\mathcal{L}}_{SP}\text{\hspace{1em}(10)}$$

采用权值衰减因子为5e-4的Adam优化器[23]和基础学习率为3.5e-4的预热策略。除了最大的VERI-WILD (120 epoch)外，我们在所有数据集上训练网络60个epoch。VeRi-776和所有人ReID数据集的批处理大小设置为128,VehicleID/VERI-WILD的批处理大小设置为512。

4.1、与其他成对损失的比较

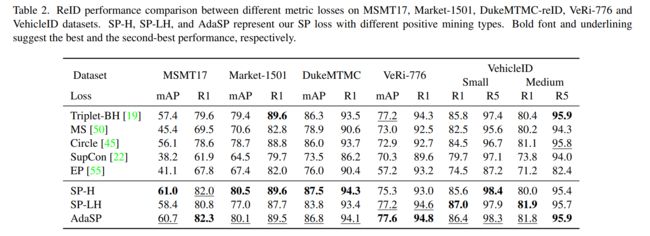
在本节中，我们首先评估并比较了MSMT17、Market-1501、DukeMTMC-reID、VeRi-776和VehicleID数据集上的SP损失与其他度量损失。为了达到一个公平的比较，我们保持相同的实验设置除了公制损失。所有数据集的实例数首先设置为8。输入的人物图像大小设置为384 × 128。性能对比见表2。可以看出，SupCon loss在所有数据集上的性能都非常有限，因为它对每个锚点都采样了所有的正对，这不仅不能增强信息对，而且很可能引入有害的三元组。尽管EP损失为每个锚挖掘了最简单的阳性，这可以避免引入有害的三元组，但它在MSMT上只能达到41.1的mAP，因为它缺乏对硬但无害的阳性对的增强。通过挖掘较低难度的正极和负极，MS损失的表现优于SupCon和EP损失，但仍落后于最佳方法。此外，triplet-BH损失和circle损失在个人ReID数据集上实现了相当的性能，因为它们基本上共享相同的挖掘策略，即每个锚的最难的正/负。对于SP损失，可以观察到SP- h损失在除VeRi-776之外的几乎所有数据集上都优于其他密集的成对损失，这表明稀疏对足以进行学习。此外，SP-H在三个行人ReID数据集上优于SPLH，而在车辆ReID数据集上获得的R1低于SP-LH。这可能是因为在每个身份有8个实例的情况下，人和车辆数据集中的大多数类分别包含小的和大的类内变化。总的来说，AdaSP在所有数据集上获得了最佳或次优性能，因为它利用动态正对来适应不同级别的类内变化。

4.2、消融研究

对不断增加的类内变化的鲁棒性。为了显示SP损失对大型类内变化的优势，我们进一步将每个标识的实例数分别从8增加到16和32。实验结果如图5所示。可以看到，在小批处理中增加每个标识的实例数后，所有度量损失都会受到性能下降的影响。这主要是因为类内的变化随着类中样本数量的增加而变得强烈。然而，在不同的度量损失之间，观察到对不断上升的类别内变化的敏感性存在显著差异。具体来说，当实例数增加到32个时，SupCon的mAP性能和EP损失下降了70%以上。圆和MS损耗也损失了30%以上的mAP性能。与其他损失相比，批处理硬挖掘的三重损失似乎对上升的类内变化不那么敏感，然而，它仍然比SP损失的三个变体表现得更差。这表明我们的SP损失，即使是最难的SPH版本，也比其他密集的成对损失对较大的类内变化更不敏感，更稳健。

此外，可以观察到，当每个身份采样8个实例时，SP-H的性能最好，而增加实例数后，SP-LH的性能下降最小。这一现象表明，最低难度的正挖掘可以大大降低对不断增加的类内变化的敏感性。AdaSP同时吸收了SP-H和SP-LH的优点，在扩大类内变异后，获得了最好的mAP性能。在VeRi-776数据集上也可以得出类似的结果，如补充资料中的图S1所示。

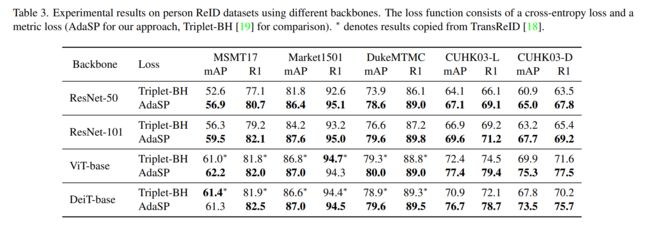
推广到不同的网络。为了证明SP损失与身份损失相结合时在提高ReID性能方面的优势，我们用AdaSP取代了三元组损失，并在四人ReID数据集上使用不同的网络实现了广泛的评估。输入图像的大小设置为256 × 128。实验结果如表3所示。结合交叉熵损失，AdaSP在几乎所有数据集和所有网络上都优于三重熵损失。特别是ResNet- 50和ResNet-101，在每个数据集上观察到超过3%的mAP改进。ResNet50-IBN, ResNet-152和MGN[48]的其他结果显示在Tab中。补充材料中的S2。这些令人鼓舞的实验结果表明，所提出的AdaSP损失能够跨不同的网络架构为行人实例生成判别特征表示，并可以取代三元组损失，有效地与交叉熵损失一起工作。

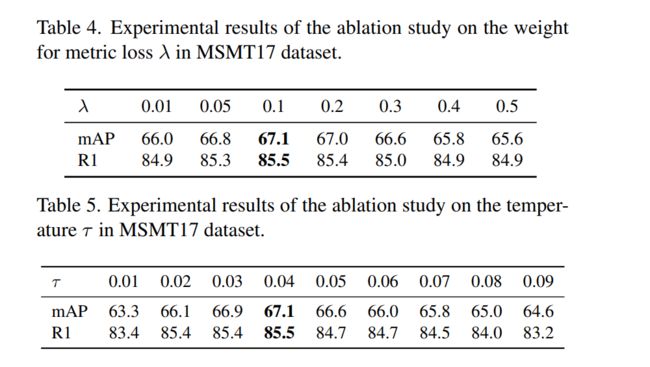
超参数的影响。在本节中，我们将探讨超参数的影响，包括公式10中SP损失的权重λ及其温度τ，对行人和车辆ReID数据集的影响。我们首先将MSMT17的λ从0.01改变到0.5。实验结果如表4所示，总体性能对λ权重不敏感，λ为[0.05,0.3]时mAP仍能保持在66.5以上，λ为0.1时性能最好。然后将温度$\tau$配置为0.01 ~ 0.09，间隔为0.01，实验结果如表5所示。可以看出，温度为0.04时mAP性能最好。然后，我们在VeRi- 776数据集上进行了类似的实验，以探索超参数对车辆ReID任务的影响。实验结果如表所示。S3和Tab。辅助材料S4。最佳mAP是在温度0.05和失重0.5的情况下实现的。在上述参数研究的基础上，本文所有实验均采用最优超参数。

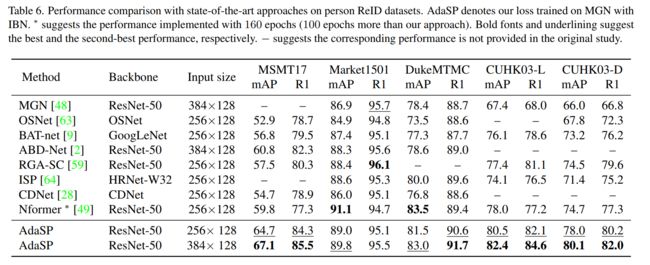
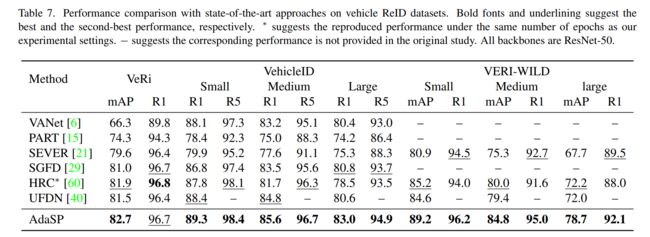
我们将AdaSP损失与基于CNN网络架构的最先进的ReID方法进行了比较，该方法基于四个行人ReID数据集和三个车辆ReID基准。实验结果如表6和表7所示。由表6可以看出，在384 × 128输入尺寸相同的情况下，AdaSP的性能明显优于MGN和ABD-Net。与其他输入尺寸为256 × 128的方法相比，AdaSP在MSMT17和cuhk03 - 3数据集上的最佳mAP分别为64.7和78.0，分别比SOTA方法Nformer提高4.9%和3.3%。对于车辆ReID基准测试，我们的方法在所有数据集的几乎所有评估指标上都达到了最佳性能。特别是对于最大的数据集VERI-WILD, AdaSP在三个测试集的mAP性能上优于HRC[60]和UFDN[40]至少4%。

5、结论

在本文中，我们提出了一种稀疏的成对损失，它只需要为一个小批中的每个类挖掘一个正对和一个负对来形成度量损失项。为了避免从具有较大类内变异的身份中抽取有害的正对，我们开发了一种最小难度的正挖掘方法，并进一步赋予其自适应策略。我们在人员和车辆ReID数据集上对拟议的SP/AdaSP损失进行了仔细评估。定量实验结果表明，我们的损耗优于当前的度量损耗，并在大多数基准上实现了最先进的性能。