斐波那契的矩阵快速幂
斐波那契数列为例 an=an-1+an-2
我们的目的是通过矩阵乘法,求得斐波那契数列的第n项,为了得到这个结果,我们还需要由[an-2 an-1]推得[an-1 an]
我们设[an-2an-1]为矩阵A,因为A1×2B2×2=C1×2,所以C与A是同规模的矩阵
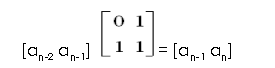
代码(来自CHC大神)
#include <cstdio>
using namespace std;
#define N 2
#define MOD 10000
//斐波那契的矩阵快速幂
// a = a * b
void matric_mul(int a[][N],int b[][N])
{
int i,j,k;
int tmp[N][N]={0};
for(i=0;i<N;i++)
{
for(j=0;j<N;j++)
{
for(k=0;k<N;k++)
{
tmp[i][j] = (tmp[i][j]+a[i][k]*b[k][j]);
}
}
}
for(i=0;i<N;i++)
{
for(j=0;j<N;j++)
{
a[i][j] = tmp[i][j];
}
}
}
int quickpow(int n){
//int ans=1,tmp=base;
int ans[2][2]={{1,0},{0,1}};
int tmp[2][2]={{0,1},{1,1}};
while(n){
if(n&1) matric_mul(ans,tmp);
matric_mul(tmp,tmp);
n>>=1;
}
for(int i=0;i<N;i++){
for(int j = 0;j<N;j++)
printf("%d\t",ans[i][j]);
printf("\n");
}
return ans[0][1];
}
int main()
{
int n;
while(~scanf("%d",&n)&&n!=-1)
printf(" f[%d] = %d\n",n,quickpow(n));
return 0;
}