BZOJ 1449 球队收益(最小费用最大流)
题目链接:http://61.187.179.132/JudgeOnline/problem.php?id=1449
题意:

思路:首先,我们假设后面的M场比赛两方都是输的,即初始时的lose[i]再加上i参加的场次。这样,后面对于i,每赢一场的收益增加值为:
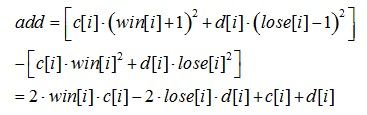
之后win[i]++,lose[i]--。至此,我们得到建图的方法:
(1)源点到每场比赛连流量1,费用0;
(2)每场比赛向双方连流量1,费用0;
(3)每个人到汇点连x条边(x为该人在M场比赛中出现的次数),流量1,费用为上面计算出的add值。每条边的add值是不同的。
最后计算最小费用再加上初始时的收益就是答案。
struct node
{
int u,v,next,cost,cap;
};
node edges[N*50];
int head[N],e;
void add(int u,int v,int cap,int cost)
{
edges[e].u=u;
edges[e].v=v;
edges[e].cap=cap;
edges[e].cost=cost;
edges[e].next=head[u];
head[u]=e++;
}
void Add(int u,int v,int cap,int cost)
{
add(u,v,cap,cost);
add(v,u,0,-cost);
}
int pre[N],F[N],C[N],visit[N];
int SPFA(int s,int t,int n)
{
int i;
for(i=0;i<=n;i++) F[i]=0,C[i]=INF,visit[i]=0;
queue<int> Q;
Q.push(s); F[s]=INF; C[s]=0;
int u,v,cost,cap;
while(!Q.empty())
{
u=Q.front();
Q.pop();
visit[u]=0;
for(i=head[u];i!=-1;i=edges[i].next)
{
if(edges[i].cap>0)
{
v=edges[i].v;
cost=edges[i].cost;
cap=edges[i].cap;
if(C[v]>C[u]+cost)
{
C[v]=C[u]+cost;
F[v]=min(F[u],cap);
pre[v]=i;
if(!visit[v]) visit[v]=1,Q.push(v);
}
}
}
}
return F[t];
}
i64 MCMF(int s,int t,int n)
{
int i,x,temp;
i64 ans=0;
while(temp=SPFA(s,t,n))
{
for(i=t;i!=s;i=edges[pre[i]].u)
{
x=pre[i];
ans+=edges[x].cost*temp;
edges[x].cap-=temp;
edges[x^1].cap+=temp;
}
}
return ans;
}
int n,m,win[N],lose[N],c[N],d[N];
int det[N],S,T;
int cal(int i)
{
int temp=2*win[i]*c[i]-2*(lose[i]+det[i])*d[i]+c[i]+d[i];
win[i]++;
det[i]--;
return temp;
}
int main()
{
RD(n,m);
int i;
i64 ans=0;
FOR1(i,n)
{
RD(win[i],lose[i]),RD(c[i],d[i]);
}
int x[N],y[N];
FOR1(i,m)
{
RD(x[i],y[i]);
det[x[i]]++; det[y[i]]++;
}
FOR1(i,n) ans+=c[i]*sqr(win[i])+d[i]*sqr(lose[i]+det[i]);
S=0; T=n+m+1;
clr(head,-1);
FOR1(i,m) Add(S,i,1,0),Add(i,m+x[i],1,0),Add(i,m+y[i],1,0);
int j,k;
FOR1(i,n)
{
k=det[i];
FOR1(j,k) Add(m+i,T,1,cal(i));
}
ans+=MCMF(S,T,T+1);
PR(ans);
}