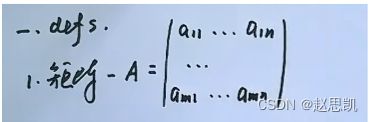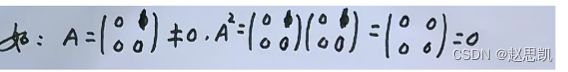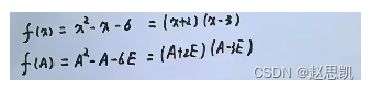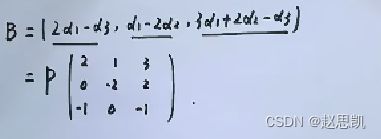线性代数2:矩阵(1)
目录
矩阵:
矩阵的定义:
0矩阵
方阵
同型矩阵:
矩阵相等的判定条件
矩阵的三则运算:
乘法的适用条件
矩阵与常数的乘法:
矩阵的乘法:
矩阵的乘法法则:
Note1:
Note2:
Note3:
向量与矩阵的关系:
转置矩阵:
矩阵多项式:
矩阵的重要性质:
性质2:
性质3:
矩阵在研究什么?
矩阵:
矩阵的定义:
矩阵和行列式的相同点以及不同点:
矩阵的行和列的个数m和n可以不同,行列式的必须相同。
行列式本质就是一个常数,而矩阵的本质是一个图标。
0矩阵
对于一个矩阵,当矩阵中所有的元素都为0时,我们才称这个矩阵为0矩阵。
方阵
行数和列数相等的矩阵就叫做方阵。
同型矩阵:
两个不同的矩阵A和B,A的行和B的行相等,A的列和B的列也相同,这样的两个矩阵就叫做同型矩阵。
矩阵相等的判定条件
对于两个同型矩阵,当他们内部的元素也全部相等时,我们就说这两个矩阵是相等的。
矩阵的三则运算:
矩阵的三则元素包括加减乘,因为我们矩阵的本质是图标,图标的相除是没有意义的。
乘法的适用条件
对于两个同型矩阵之间,我们可以使用加减法。同型矩阵可以相加减。
矩阵之间的加减法法则是对应元素相加减即可。
矩阵与常数的乘法:
常数乘以矩阵等价于矩阵中的每一个元素都乘以常数。
结合我们之前学习的行列式,我们可以得出一个结论:我们知道,行列式的公共因子是从可以从某一行或者某一列中提取出来,而矩阵的公共因子必须从矩阵中的所有元素中提取出来。
矩阵的乘法:
对于这两个矩阵,我们可以发现A矩阵的列数等于B矩阵的行数,所以我们就可以用A*B。
简计:内标相同可以乘。
乘出来的结果也是一个矩阵,这个矩阵的行数和列数则是由第一个矩阵的行数和第二个矩阵的列数来决定的。
简计:外标决定行列式的型。
矩阵的乘法法则:
我们可以这样记忆:C11表示矩阵的第一个元素,他的结果是由A矩阵的第一行元素分别×B矩阵的第一列元素之和。
所以Cmn的计算方法是由A矩阵的第m行元素分别与B矩阵的第n行元素相×再相加的结果。
Note1:
两个数只要有一个为0就可以得出两个数的乘积为0,但是我们的矩阵并不是一个数,矩阵是一个图标。
Note2:
Note3:
向量与矩阵的关系:
向量一定是矩阵,是矩阵的一种,默认使用向量就是列向量,我们可以把向量α理解为n行1列的矩阵。
转置矩阵:
转置矩阵就是把原矩阵的行和列进行颠倒即可。
我们可以发现,一个转置向量*一个普通向量的结果是一个常数。
那么我们用一个普通向量*一个转置向量的结果是什么呢?
我们可以发现,一个普通向量*一个转置向量的结果是一个方阵。
简记:两向量相乘,左转置为常数,右转置为方阵。
矩阵多项式:
我们把一个x的n次多项式与一个n阶方阵进行综合,得出结果:
E则表示矩阵的最小单位,E的写法如下:
对于矩阵多项式来说,我们也可以因式分解:
矩阵的重要性质:
我们进行推导
这里有两个矩阵:一个是m行n列,一个是n行s列,所以A*B是合法的,我们先对矩阵B进行列化,列化的过程如下:
如图所示,第一个五角星的结果为A的第一行×B1,第二个五角星的结果为A的第二行×B1等等。
所以第一行的五角星可以代表B1×A的全部元素,也就是B1×A。
性质2:
有三个向量,矩阵P是由三个向量组成的矩阵。
我们怎么用P来表示出矩阵B呢?
性质3:
我们把这个矩阵中的元素提取出来,放到行列式里面去。
我们在这个行列式中任取一个元素,该元素的行数和列数分别是i和j,我们删除掉这一行和这一列,就能够得到一个余子式Mij
这个余子式是n-1阶的。
根据余子式和对应的行列数,我们可以求出对应的代数余子式:
我们把求出来的代数余子式的行列数进行颠倒放进一个矩阵中。
求出来的这个矩阵就叫做伴随矩阵,求伴随矩阵的方法是先取出矩阵A的所有元素到行列式A中去,然后求出这个行列式的所有代数余子式,并把这些代数余子式行列数进行颠倒放进矩阵中去,这个矩阵就叫做伴随矩阵,
那么用原矩阵×伴随矩阵的结果是多少呢?
我们知道一个性质:用行列式的第n行(列)元素乘以第n行(列)元素的代数余子式的结果就是行列式的值,而用第n行(列)元素分别乘以第m(m≠n)行(列)的结果就是0,所以我们可以求出结果。
矩阵在研究什么?
我们分别写两个线性方程组。
我们把第一个方程组的系数拎出来可以构成是一个矩阵:
我们再把所有的未知数拎出来,可以构成一个列:
而A与x的内标相同,可以用A*X。
计算出来的是矩阵是m行1列的矩阵。
所以计算出来的结果就是这个齐次方程组。
而AX=0表示AX的结果为0矩阵。
所以用这两个矩阵相×就可以表示出齐次方程组。
而对于非齐次方程组,那么AX=b,我们也可以把b化成矩阵的形式:
所以AX等于b就等价于: