清风建模-皮尔逊相关检验

目录

前言

一、皮尔逊相关系数是什么？

二、皮尔逊相关系数如何计算？

        1.前提条件

2.检查数据是否是正态分布

3.皮尔逊相关系数的计算

4.对皮尔逊相关系数进行假设检验

总结

---

---

前言

       面对一批数据进行分析和建模，首先需要掌握参数估计和假设检验这两个数理统计的最基本方法，给定的数据满足一定的分布要求后才能建立回归分析和方差分析等数学模型。本文介绍皮尔逊相关系数的假设检验和它的适用条件。

一、皮尔逊相关系数是什么？

        在统计学中，皮尔逊相关系数，是用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间，其绝对值越大说明该两个变量越相关。

注意：该系数只能评价两个线性变量之间的相关性。

二、皮尔逊相关系数如何计算？

1.前提条件

1.         在计算皮尔逊相关系必须用spss数前（推荐用spss24及之后的版本）画出各个变量之间的散点图（相关性可视化）。当然也可以用其他软件，如excel，matlab。若两个变量的散点图呈线性的关系，则可以用皮尔逊相关系数。反之，则不能用。
2.         然后再判断总体数据是否满足正态分布。例如：如果你要比较5个变量两两的相关性，这时就要进行判断，方法有很多种，后面会提到。

注意：若以上条件有一不满足，则不能用皮尔逊相关系数。 

2.检查数据是否是正态分布

        可能很多小伙伴很疑惑为什么要判断数据是否是正态分布，因为我们要对皮尔逊相关系数进行假设检验。那为什么要进行皮尔逊相关假设检验？因为这是为了要证明相关不是因为抽样的偶然性造成的。那它的假设检验又怎么和数据是否正态分布扯上了关系，因为我们在求得皮尔逊相关性系数后，通常还会用t检验之类的方法来进行皮尔逊相关性系数检验， 而t检验是基于数据呈正态分布的假设的。t检验又是什么玩意？t检验，亦称student t检验（Student's t test），主要用于样本含量较小，总体标准差σ未知的正态分布。

1. 正态分布JB检验（大样本 n>30）

上面写了这么多，可以用matlab来实现，0.05是我们因为我们假设置信度为0.95。

MATLAB中进行JB检验的语法：[h,p] = jbtest(x,alpha) 当输出h等于1时，表示拒绝原假设；h等于0则代表不能拒绝原假设。 alpha就是显著性水平，一般取0.05，此时置信水平为1‐0.05=0.95 。x就是我们要检验的随机变量，注意这里的x只能是向量。

% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)

% 用循环检验所有列的数据
n_c = size(Test,2);  % number of column 数据的列数
H = zeros(1,6);  % 初始化 节省时间和消耗
P = zeros(1,6);

for i = 1:n_c
    [h,p] = jbtest(Test(:,i),0.05);
    H(i)=h;
    P(i)=p;
end
disp(H)
disp(P)

Text为存放数据的矩阵。

2.Q-Q图 

要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点 是否近似地在一条直线附近。（要求数据量非常大）

3.小样本3≤n≤50：Shapiro-wilk检验

3.皮尔逊相关系数的计算

       皮尔逊相关系数的计算 ，matlab种有corrcoef函数（correlation coefficient相关系数）。 R = corrcoef(A) ，返回 A 的相关系数的矩阵，其中 A 的列表示随机变量（指标），行表示观测值（样本）。 R = corrcoef(A,B) 返回两个随机变量 A 和 B （两个向量）之间的系数。 我们要计算体测的n个指标之间的相关系数，只需要使用下面这个语句： R = corrcoef(Test)。%Text为保存文件的矩阵。

4.对皮尔逊相关系数进行假设检验

附上matlab代码：

%% 假设检验部分
x = -4:0.1:4;
y = tpdf(x,28);  %求t分布的概率密度值 ,28是自由度，28为n-2，上面我们假设 n= 30.
figure(1)
plot(x,y,'-')
grid on  % 在画出的图上加上网格线
hold on  % 保留原来的图，以便继续在上面操作
% matlab可以求出临界值，函数如下
tinv(0.975,28)    %    2.0484
% 这个函数是累积密度函数cdf的反函数
plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')

计算各列之间的相关系数以及p值 ,一行代码：[R,P] = corrcoef(Test)   R返回的是相关系数表，P返回的是对应于每个相关系数的p值。%Test为存放数据的矩阵。

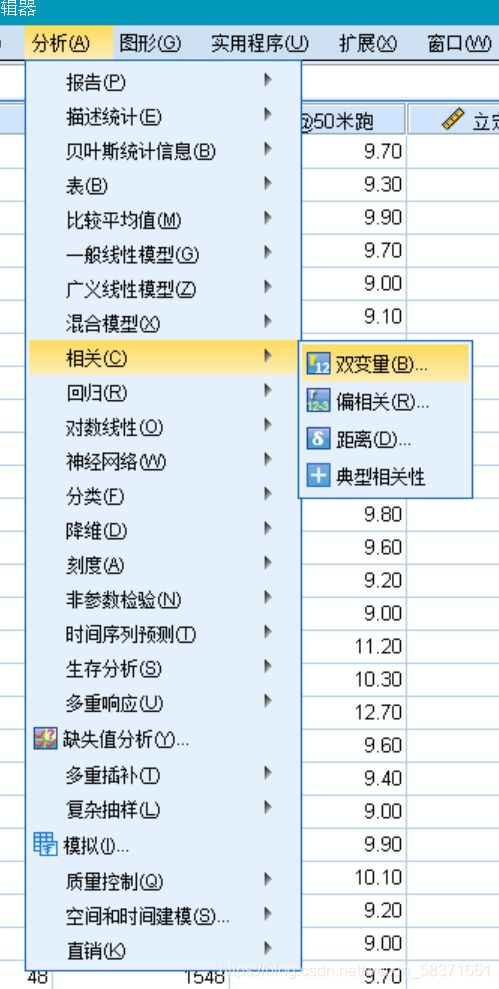
可以用spss软件进行求解，具体步骤

显著意思就是拒绝原假设。

总结

要用皮尔逊相关系数必须满足连续数据，正态分布，线性关系。