【ARIMA-WOA-LSTM】差分自回归移动平均方法-鲸鱼优化算法-LSTM预测研究(python代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Python代码实现
1 概述
差分自回归移动平均模型(ARIMA)是一种广泛应用于各领域的预测模型1-19],主要包含自回归模型和移动平均模型2个部分。自回归模型的阶数为p,信号差分的阶数为d,移动平均模型的阶数为q,因此模型通常表示成ARIMA( p,d ,q) ,具体的数学表达式为:
 ARIMA模型的具体实现过程如下:
ARIMA模型的具体实现过程如下:
(1)对所研究的时间序列数据进行平稳性验证,如果不满足要求,则对其进行d阶差分转换成平稳时间序列。
(2)通过自相关系数图和偏自相关系数图以及贝叶斯信息准则[201确定阶数p 和q。
(3)采用确定好阶数的ARIMA(p , d ,q)拟合时间序列,并根据预测后的数据和原时间序列进行结果统计和预测精度分析。
鲸鱼优化算法及其应用
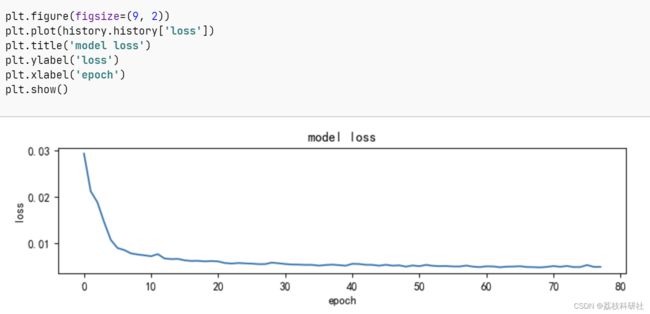
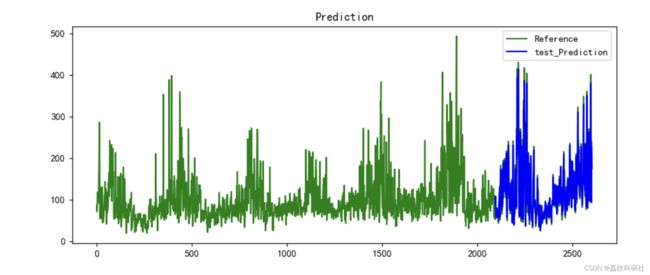
2 运行结果
# ===========主程序================
Max_iter = 3 # 迭代次数
dim = 5 # 鲸鱼的维度
SearchAgents_no = 3 # 寻值的鲸鱼的数量
# 参数的上限
UB = np.array([500, 500, 500, 0.999, 300])
# 参数的下限
LB = np.array([1, 1, 1, 0.00001, 1])
fitnessCurve, para = woa(LB, UB, dim=dim, whale_num=SearchAgents_no, max_iter=Max_iter).opt()
print('最佳参数为 ', para)
#显示预测结果
%matplotlib notebook
fig1 = plt.figure(figsize=(10, 4),dpi=100)
plt.plot(new_data, label="Reference", color='green')
plt.plot(range(len(x_train)+timestep+1,len(new_data)),draw_test, color='blue',label='test_Prediction')
plt.title('Prediction', size=12)
plt.legend()
plt.show()
plt.figure(figsize=(10, 4),dpi=100)
plt.plot(test_data, label="Actual", color='red',linewidth=4)
plt.plot(range(len(x_train)+timestep+1,len(new_data)),draw_test, color='blue',label='Prediction',linewidth=2.5,linestyle="--")
plt.title('ARIMA-LSTM Prediction', size=15)
plt.ylabel('AQI',size=15)
plt.xlabel('time/day',size=15)
plt.legend()
plt.show()
3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]岑威钧,王肖鑫,蒋明欢.基于EEMD-LSTM-ARIMA的土石坝渗压预测模型研究[J].水资源与水工程学报,2023,34(02):180-185.
[2]沈露露,梁嘉乐,周雯.基于ARIMA-LSTM的能量预测算法[J].无线电通信技术,2023,49(01):150-156.
[3]曹梦茜,郑东健.基于FCM-WOA-LSTM的大坝变形预测模型及其应用[J].水电能源科学,2023,41(05):71-75.DOI:10.20040/j.cnki.1000-7709.2023.20221887.