Keras中 LSTM 模型解读

LSTM模型

图中看起来是三个cell，其实是一个cell在不同时刻上的拼接，也就是说其实是一个cell在不同时刻的状态。我们就以中间那个cell为例进行说明吧。
其中，四个黄色的小矩形就是普通神经网络的隐藏层结构，其中第一、二和四的激活函数是sigmoid，第三个的激活函数是tanh。t时刻的输入X和t-1时刻的输出h(t-1)进行拼接，然后输入cell中，其实可以这样理解，我们的输入X(t)分别feed进了四个小黄矩形中，每个小黄矩形中进行的运算和正常的神经网络的计算一样（矩阵乘法），有关记忆的部分完全由各种门结构来控制（就是0和1），同时在输入时不仅仅有原始的数据集，同时还加入了上一个数据的输出结果，也就是h(t-1)，那么讲来LSTM和正常的神经网络类似，只是在输入和输出上加入了一点东西。cell中可以大体分为两条横线，上面的横线用来控制长时记忆，下面的横线用来控制短时记忆。

输入

下面我们就来说说输入问题，在Keras中，LSTM的输入shape=(samples, time_steps, input_dim)，其中samples表示样本数量，time_steps表示时间步长，input_dim表示每一个时间步上的维度。我举一个例子吧，现在有一个数据集有四个属性(A，B, C, D)，我们希望的预测标签式D，假设这里的样本数量为N。如果时间步长为1，那么此时的输入shape=(N, 1, 4)，具体的数据是这样的[A(t-1), B(t-1), C(t-1), D(t-1)]（此处表示一个数据样本），样本标签为[D(t)]；如果时间步长为2，那么此时的输入shape=(N, 2, 4)，具体的数据是[[A(t-2), B(t-2), C(t-2), D(t-2)], [A(t-1), B(t-1), C(t-1), D(t-1)]]（此处仍表示一个样本数据）。

输出

关于Keras中LSTM的输出问题，在搭建网络时有两个参数，一个output_dim表示输出的维度，这个参数其实就是确定了四个小黄矩形中权重矩阵的大小。另一个可选参数return_sequence，这个参数表示LSTM返回的时一个时间序列还是最后一个，也就是说当return_sequence=True时返回的是(samples, time_steps, output_dim)的3D张量，如果return_sequence=Flase时返回的是(samples, output_dim)的2D张量。比如输入shape=(N, 2, 8)，同时output_dim=32，当return_sequence=True时返回(N, 2, 32)；当return_sequence=False时返回(N, 32)，这里表示的时输出序列的最后一个输出。
关于return_sequence的理解：即返回序列，若为true，则说明后面还有LSTM模型需要接收序列，即存在步长，若为false，说明不需要接收模型，则没有步长这个参数。

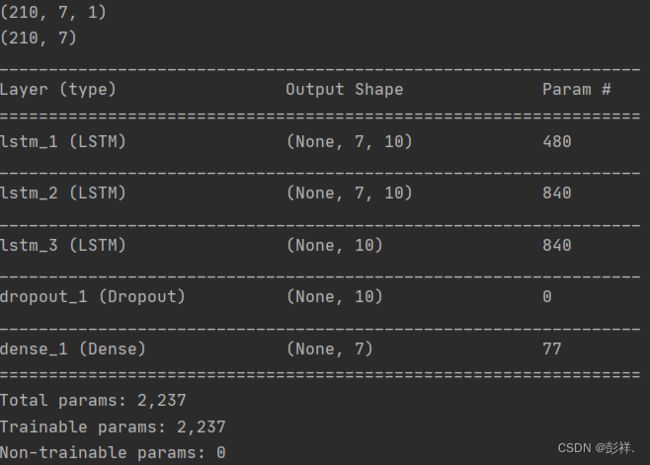
	model = Sequential()
    model.add(LSTM(10, activation='relu', return_sequences=True, input_shape=(n_input, n_features)))
    model.add(LSTM(10, activation='relu', return_sequences=True, dropout=0.2, recurrent_dropout=0.2))
    model.add(LSTM(10, activation='relu', return_sequences=False,dropout=0.2, recurrent_dropout=0.2))
    #Error when checking target: expected dense_1 to have 3 dimensions, but got array with shape (207, 7)
    # model.add(Conv1D(128, 8, padding='same'))
    model.add(Dropout(0.8))
    model.add(Dense(n_out))
    model.summary()

这里我们设置LSTM神经元个数为10，方便计算：

通过上面的推导我们发现，其实实际的参数量和步长是没有关系的，这一点我也验证了一下，通过改变输入shape=(samples, time_steps, input_dim)中的time_stpes的值，参数量不会发生变化。