Matleb学习--图论最短路径问题

1.图论：

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。
图论可分为两种图，有向图和无向图。顾名思义，即连接两点之间的线是否有箭头。在笔者看来，无向图也属于有向图的一种，不过是有向图连接两点之间的线为双向箭头罢了。

2. 画图的两种方法：

1. 网站在线画图（推荐）点我进入网站
   进入网站后界面如下：
   首先说一下其中必要处的功能

Node Count:	设置点数，即右方圆圈个数
Graph Data:	单列数字为写出圆圈内的数字点数（单列数字个数之和即为Node Count），双列数字为确定圆圈之间关系，也可增加到三列，即增加权重一项，具体演示可看下文
0（1）-index	圆圈内最低数字从0（1）开始
Download as PNG	以图片格式导出
Undirected(Directed)	无向图（有向图）

然后对部分功能做出解释
**单列数字功能以及和Node Count关系

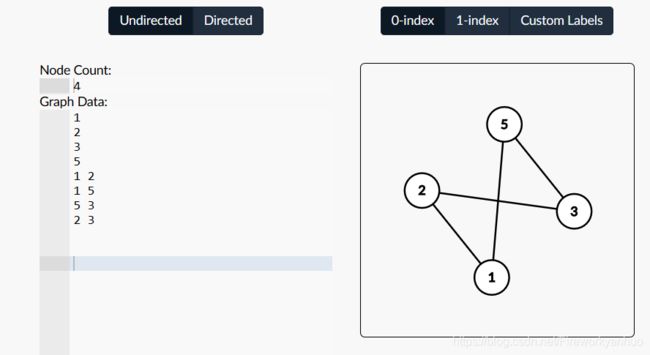
**双列数字的功能（千万注意空格）

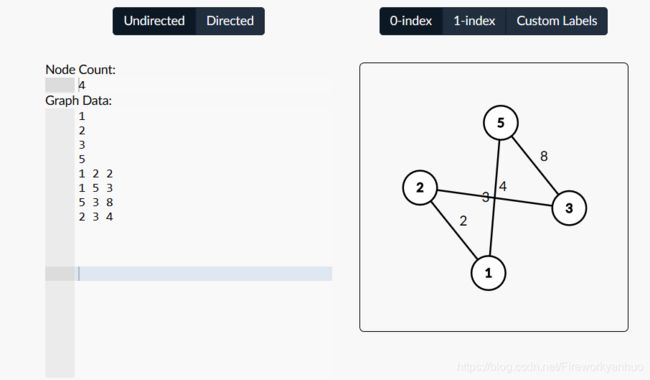
**加入权重的图论

**带箭头的图论

2. Matleb制图
   先上代码，代码能看懂的可直接移步第三部分。（代码来自清风老师，侵权可删）

%% Matlab作无向图
% （1）无权重（每条边的权重默认为1）
% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图
% s 和 t 都必须具有相同的元素数；这些节点必须都是从1开始的正整数，或都是字符串元胞数组。
s1 = [1,2,3,4];
t1 = [2,3,1,1];
G1 = graph(s1, t1);
plot(G1)
% 注意哦，编号最好是从1开始连续编号，不要自己随便定义编号

% 注意字符串元胞数组是用大括号包起来的哦
s2 = {'学校','电影院','网吧','酒店'};
t2 = {'电影院','酒店','酒店','KTV'};
G2 = graph(s2, t2);
plot(G2, 'linewidth', 2)  % 设置线的宽度
% 下面的命令是在画图后不显示坐标
set( gca, 'XTick', [], 'YTick', [] );  

% （2）有权重
% 函数graph(s,t,w)：可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = graph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  

%% Matlab作有向图
% 无权图 digraph(s,t)
s = [1,2,3,4,1];
t = [2,3,1,1,4];
G = digraph(s, t);
plot(G)
set( gca, 'XTick', [], 'YTick', [] );  

% 有权图 digraph(s,t,w)
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = digraph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  

函数说明

graph(s,t)	可以在s和t中的对应节点之间创建边，并生成一个图
graph(s,t,w)	可以在s和t中的对应节点之间以w的权重创建边，并生成一个图

其他代码注释已给详细，看代码实践即可。

3.权重邻接矩阵

权重邻接矩阵即将图论用矩阵表示出来，自身与自身关系为0，自身与其他无关系的为无穷大（Inf）,有关系的即为权重。权重邻接矩阵按图论分类也可分为有向图的权重邻接矩阵和无向图的权重邻接矩阵。两者之间主对角线上元素均为零，Dij表示第i个节点到第j个节点的权重。区别无向图为对称矩阵，有向图一般不是对称矩阵。最后二图顶千言。