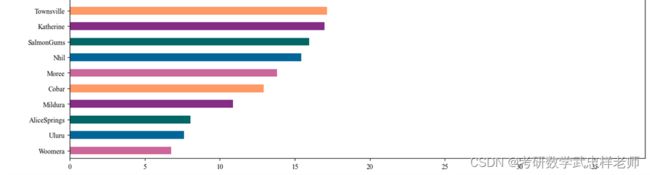Can We Predict Australian Rainfall?建立LSTM模型预测澳大利亚平均降雨量

数据集：Rain in Australia | Kaggle

数据探索

首先df =pd.read_csv('weatherAUS.csv')读入数据，df.shape查看形状为(145460, 23)。

通过df['RainTomorrow'].value_counts(dropna=False)查看下雨与不下雨标签各自的数量，No为110316，Yes为31877，NaN为3267。

通过df.RainTomorrow.fillna('null').value_counts(normalize=True)统计各标签占比，发现Yes占75.84%，No占21.91%，NaN占2.25%，有轻微的样本不均衡问题，但不是很严重。

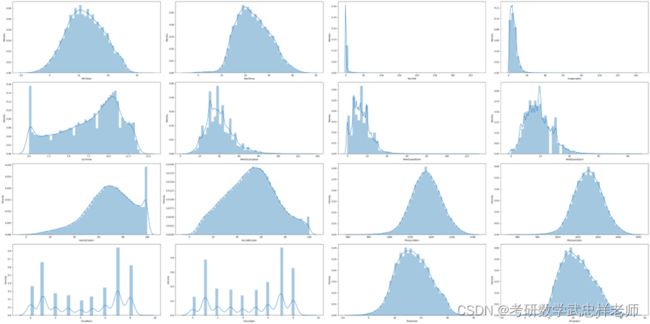
接下来通过df[i].dtype=='float64'找出所有数值型数据并绘制分布：

发现有部分数值型数据呈偏态分布。

下面绘制最近1000天的最高和最低气温，发现季节特征明显：

绘制相关性热力图，发现Temp9am、Temp3pm、Pressure3pm等属性相关性较强，可以只保留其中的一个，删除其余属性。

 

下面统计每个城市下雨天数和非下雨天数的百分比并按从高到低排序。可以看出排名前列的Portland、Walpole、Cairns等地大多位于澳洲东西沿海，为亚热带气候或海洋性气候，较为湿润；而排名靠后的Woomera、Uluru、Mildura等地大多身居内陆，为热带沙漠气候，较为干旱少雨。 

 

接下来探索气压与是否下雨的关系。下面的散点图横纵坐标分别为两个时间点的气压值，发现气压越低越容易下雨，这与常识符合。

 

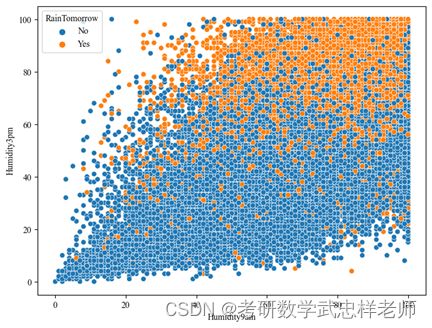
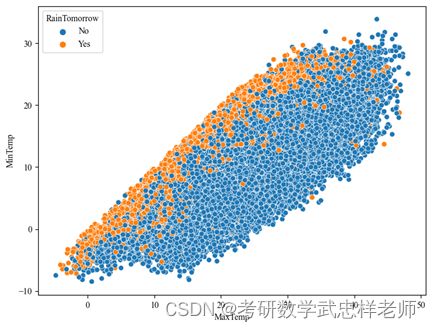
我们再来探索湿度和温度对是否下雨的影响，发现湿度越高、温差越小越容易下雨：

 

 

数据预处理

去除空值

通过weather = weather.dropna(axis = 0,subset = ['RainTomorrow'])删除标签为空值的行。

缺失值填充

一般而言，对于类别型变量，采用众数填充；对数值型变量采用中位数或平均数填充。

使用XGBoost进行特征筛选

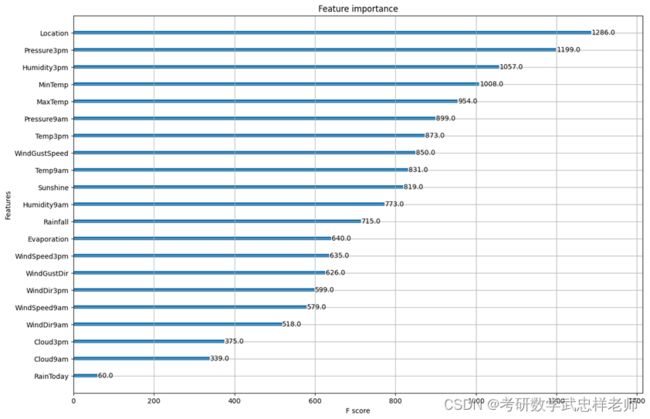
重要性分数，衡量了特征在模型中的提升决策树构建中的价值：一个属性越多的被用来在模型中构建决策树，它的重要性就相对越高。属性重要性是通过对数据集中的每个属性进行计算并排序得到的。在单个决策树中通过每个属性分裂点改进性能度量的量来计算属性重要性，由节点负责加权和记录次数。意即一个属性对分裂点改进性能度量越大（越靠近根节点），权值越大、被越多提升树所选择，属性就越重要。性能度量标准可以是选择分裂节点的Gini纯度，也可以是其他度量函数。最终将一个属性在所有提升树中的结果进行加权求和后然后平均，得到重要性得分。一个已训练的Xgboost模型能够自动计算特征重要性，并通过plot_importance()绘制：

特征编码

主要使用了sklearn.preprocessing中的LabelEncoder、OrdinalEncoder和OneHotEncoder对特征和标签进行编码。

Ordinal Encoding是最简单的一种思路，对于一个具有m个类别的特征 ，我们将其对应地映射到 [0，m−1] 的整数。

LabelEncoder() 用于标签编码，而数据的标签一般只有一维，所以其编码的数据维度应为 (n_samples,)。

独热编码是非常常用的一种编码方式，对于一个具有m个类别的特征，我们将其扩展为一个m维的向量，向量的各个分量与各个类别一一对应。对于属于第i个类别的特征，其对应向量中第i维为 1 ，其他各维为 0 。意即这m维分量是互斥的，每次只有一个维度被激活，对应其类别。独热编码很自然地解决了 LabelEncoder 所要求的特征内在顺序的限制，并且经过独热编码后，特征变成稀疏的了，这有两个好处：解决了分类器不好处理属性数据的问题；在一定程度上也起到了扩充特征的作用。但独热编码的问题也很明显：编码后会使得空间维度大大增加，尤其在类别很多的时候，这会使得训练难以进行（当然此时也可以考虑使用PCA降维等方法缓解特征空间庞大的问题）。

LSTM时间序列预测

滑动窗口

时间序列数据可以转化为监督学习问题。可以使用前面的时间步（time steps）作为输入变量，下一个时间步作为输出变量。pandas中的shift()函数可以完成这一转换。使用之前的时间点的值来预测下一个时间点的值骤称为滑动窗口方法（sliding window method），在一些文献中，也称为窗口方法（window method）。包含时间点的个数称为窗口宽度（window width）或延迟大小（size of the lag）。滑动窗口是将时间序列数据转换成监督学习问题的基础。

时间序列分解

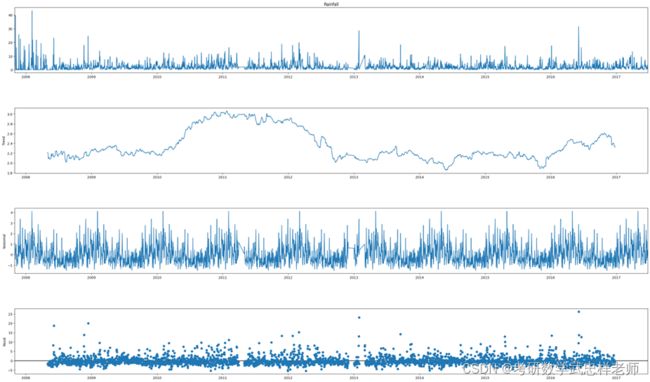
时间序列的数据往往会呈现出周期性变化的规律，这种周期性变化规律往往是由季节性因素所带来的。如果时间序列数据的时间颗粒度是时刻（如小时）,那它的季节性周期有可能是24，如果时间颗粒度是天，那季节性周期有可能是7，如果时间颗粒度是月，那季节性周期有可能是12，如果时间颗粒度是季度，那它的季节性周期有可能是4。下面我们调用statsmodels.tsa.seasonal中的seasonal_decompose函数对澳洲降水数据进行时间序列分解。

日粒度下的时间序列分解 

月粒度下的时间序列分解

搭建网络

我们的预测任务是降水量，这是一个连续值，因此属于回归问题。在Keras中，LSTM的数据格式要求为 [样本，时间步长，特征]三元组，我们首先对数据集进行形状转换，再搭建LSTM网络。因为是回归问题，所以全连接层的输出为1，损失函数指定为MAE（平均绝对误差），优化器为Adam。

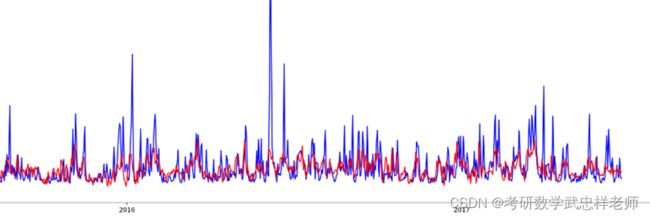
其中红线为预测值，其变化趋势与真实值（蓝线）大致拟合。 

部分代码：

# LSTM时间序列预测：指定城市的降水量
def run_preds_city(df, city, groupby='Date'):
    
    df = df.loc[df['Location'] == city]
    
    category_col = [x for x in df.columns if df[x].dtype == 'object']

    for name in category_col:
    # 对类别型数据进行编码
        enc = sklearn.preprocessing.LabelEncoder()
        enc.fit(list(df[name].values.astype('str')) + list(df[name].values.astype('str')))
        df[name] = enc.transform(df[name].values.astype('str'))
    
    # 时间序列预测可以被认为是监督学习问题 
    # 将序列向前移动一个时间步
    combined_df = df.groupby([groupby]).mean()
    combined_df['RainfallPred'] = combined_df['Rainfall'].shift(1)

    combined_df.drop(['Rainfall'], axis=1, inplace=True)
    #combined_df = combined_df[['Humidity3pm', 'WindGustSpeed', 'Pressure3pm', 'Sunshine', 'MaxTemp', 'WindGustDir', 'MinTemp', 'Rainfall']] 
    lstm_dataset = combined_df.values
    lstm_dataset = lstm_dataset.astype('float32')

    reframed = combined_df
    reframed.dropna(inplace=True) # 去除空值
    column_names = reframed.columns

    # 归一化   
    scaler = MinMaxScaler(feature_range=(-1, 1))
    reframed = scaler.fit_transform(reframed)   
    reframed = pd.DataFrame(reframed, columns=column_names)

    # 划分训练集和测试集  
    values = reframed.values
    forecast_period = np.round(len(values)*0.7, 0).astype(int)
    train = values[:forecast_period, :]
    test = values[forecast_period:, :]

    # 取出数据和标签    
    train_X, train_y = train[:, :-1], train[:, -1]
    test_X, test_y = test[:, :-1], test[:, -1]

    # LSTM的数据格式要求为 [样本，时间步长，特征] 三元组
    train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
    test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
  
    lstm_model = Sequential()
    lstm_model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) # 隐藏层有50个神经元
    lstm_model.add(Dense(1)) # 因为是回归问题，所以全连接层输出为1
    lstm_model.compile(loss='mae', optimizer='adam')  # 损失函数为绝对误差MAE，优化器为Adam 
     
    history = lstm_model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=1, shuffle=False) # 验证集即为测试集
    # 返回一个 History 对象。其 History.history 属性是连续 epoch 训练损失
 
    plt.figure(figsize=(6, 4))
    plt.plot(history.history['loss'], label='train',color='r') # 绘制训练集loss和测试集loss
    plt.plot(history.history['val_loss'], label='test',color='b')
    plt.legend()
    plt.show()
    
    # 预测   
    yhat = lstm_model.predict(test_X)
  
    test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
  
    inv_yhat = np.concatenate((test_X[:, 0:], yhat), axis=1)
    inv_yhat = scaler.inverse_transform(inv_yhat)
    inv_yhat = inv_yhat[:,-1]
  
    test_y = test_y.reshape((len(test_y), 1))
    inv_y = np.concatenate((test_X[:,0:], test_y), axis=1)
    inv_y = scaler.inverse_transform(inv_y)
    inv_y = inv_y[:,-1]
  
    rmse = np.sqrt(mean_squared_error(inv_y, inv_yhat)) # 均方根误差
    
    lstm_predictions = [np.nan for _ in range(0,len(train_X))]
    combined_df['LSTM Prediction'] =  lstm_predictions+list(inv_yhat)

    plt.figure(figsize=(100, 10))
    plt.title('Test RMSE: %.3f' % rmse)
    plt.plot(combined_df['RainfallPred'],color='b')
    plt.plot(combined_df['LSTM Prediction'],color='r')
    plt.show()

run_preds_city(df, 'Perth', 'Date')