马尔可夫蒙特卡洛方法(MCMC)简单理解
本文没有理论推导证明,旨在用简单的例子理解MCMC方法。
引入
p ( T ∣ D ) = p ( D ∣ T ) p ( T ) p ( D ) (1) p(T|D) = \frac{p(D|T)p(T)}{p(D)} \tag{1} p(T∣D)=p(D)p(D∣T)p(T)(1)
(1)是一个基本的贝叶斯公式, p ( T ∣ D ) p(T|D) p(T∣D)是后验值, p ( T ) p(T) p(T)是先验值, p ( D ∣ T ) p(D|T) p(D∣T)是似然值,分母是积分项,要求出后验值的话看起来计算并不复杂。
但是如果说现在有很多的参数呢
p ( T , l , k ∣ D ) = p ( D ∣ T , l , k ) p ( l ) p ( k ) p ( T ) ∫ T ∫ k ∫ l p ( D ∣ T , l , k ) p ( l ) p ( k ) p ( T ) d l d k d T (2) p(T,l,k|D) = \frac{p(D|T,l,k)p(l)p(k)p(T)}{\int_T\int_k\int_lp(D|T,l,k)p(l)p(k)p(T)dldkdT} \tag{2} p(T,l,k∣D)=∫T∫k∫lp(D∣T,l,k)p(l)p(k)p(T)dldkdTp(D∣T,l,k)p(l)p(k)p(T)(2)
对于上式,肉眼可见,我们已经不能通过解析的方式得到结果了,主要是分母的原因(二重积分已经是不容易的事,况且规范的函数才可积出来)
因此马尔科夫蒙特卡洛(MCMC)方法出现,帮我们解决后验分布的问题,就是不用计算(2)式中可怕的分母,也能得到 T , l , k T,l,k T,l,k的后验分布。
先不要管太多,假设只有一个参数 x x x,它服从正态分布 N ( 0 , 1 ) N(0,1) N(0,1),我们要近似 x x x的分布,也就是近似 N ( 0 , 1 ) N(0,1) N(0,1),先来看一下MCMC的过程
图 1 图1 图1

图 2 图2 图2
通过不断地采样,得到 x 1 , x 2 , . . . . , x n , . . . . x1,x2,....,xn,.... x1,x2,....,xn,....,用这些样本来近似 x x x的分布,这就是MCMC的作用:近似分布
接下来看细节方面。
蒙特卡洛(MCMC中第二个MC):
到底采多少样本就可以近似 x x x的后验分布呢,答案是无穷个,只要你愿意,采多少都可以,不断采样的过程就是蒙特卡洛采样。
但是,漫无目的的瞎采当然近似不到后验分布,所以出现了M-H采样,就是说,新采样本好于 x n − 1 x_{n-1} xn−1,那么保留作为 x n x_n xn,差于 x n − 1 x_{n-1} xn−1,以一定概率保留(差的都不采很有可能陷入局部最优),以一定概率舍去,舍去的话重新采样。样本的好与坏一定是有评价体系的,这可能是似然值、适应度等等,这里是 N ( 0 , 1 ) N(0,1) N(0,1)在新样本的概率密度。
M-H采样保证了样本更高概率去往正态分布的中心,更低概率去往两边。
马尔科夫(MCMC中第一个MC):
从上图中可以看到,新样本来自于且仅来自于上一个样本,跟之前的样本没关系,这就是马尔科夫链的定义。
仅仅这一个要求是不够的,没有办法保证最终能得到一个平稳的 x x x分布,那怎么才能得到 x x x的平稳分布?答案是需要一个平稳的马尔科夫链才行,平稳的马尔科夫链需要满足细致平稳条件,下面举例说明。
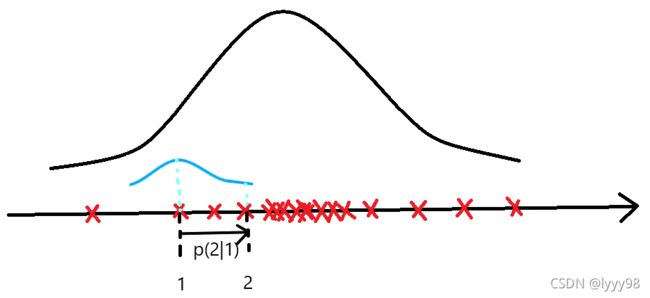
图 3 图3 图3
假设 x n − 1 x_{n-1} xn−1取值1, x n x_{n} xn取值2,2怎么来的呢,它从 p ( x ∣ 1 ) p(x|1) p(x∣1)得到, p ( x ∣ 1 ) p(x|1) p(x∣1)就是以 x n − 1 = 1 x_{n-1}=1 xn−1=1为期望,1为方差的正态分布(图3蓝色),方差是我随便给的,正态分布(图3蓝色)也可以换成其他的分布,重点是需要个确定的分布,那现在 p ( 2 ∣ 1 ) p(2|1) p(2∣1)就是定值。确定的分布可以保证每次从 1 → 2 1\rightarrow2 1→2的概率是一样的,接着想宽泛一点, 1 → 2 , 2 → − 5 , − 5 → 4 , 4 → 100 , 100 → 50 1\rightarrow2,2\rightarrow-5,-5\rightarrow4,4\rightarrow100,100\rightarrow50 1→2,2→−5,−5→4,4→100,100→50……等等,都是确定的概率,这就是细致平稳条件的要求( π P = π {\pi}P=\pi πP=π满足啦),马尔科夫链就能近似到平稳分布了。
将马尔科夫和蒙特卡洛结合起来,就能发挥强大的功效,我们采的样本就能像图3中的红色叉叉,它们很好的体现了 x x x真实的分布,下面画一个更直接的图。
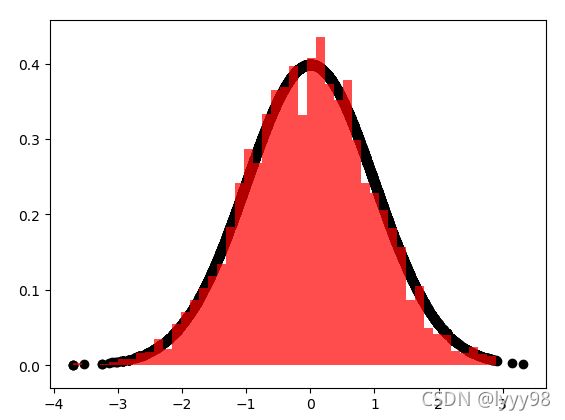
图 4 图4 图4
Gibbs采样
以上我们只近似了 x x x的分布,如果现在有两个维度呢,需要近似 π ( x , y ) \pi(x,y) π(x,y)呢?采样该怎么采,这也不难,先采 x 1 x_1 x1,再根据 P ( y ∣ x 1 ) P(y|x_1) P(y∣x1)采 y 1 y_1 y1,再根据 P ( x ∣ y 1 ) P(x|y_1) P(x∣y1)采 x 2 x_2 x2,……这样我们就采到了 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1,y_1),(x_2,y_2),(x_3,y_3) (x1,y1),(x2,y2),(x3,y3)……过程如下图。
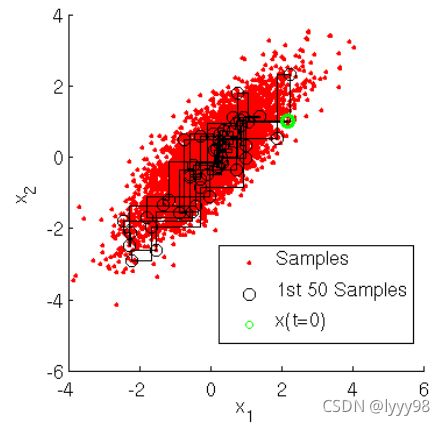
图 5 图5 图5
图5截自刘建平老师的博客.
该博客有更详细的理论推导,本文中的例子也参考了该博客中的实例。