卷积神经网络
卷积神经网络
1. 从多层感知机到卷积神经网络
有了多层感知机之后,我们应该怎么做CV(Computer Vision)任务呢?一种简单的想法是把图像看成一维张量直接输入到一个多层感知机里。
这样可以吗?当然可以,早期的CV就是这么做的,但是有啥问题呢?主要有2个方面:
问题1:参数量太大了。
问题2:无法利用图像的空间位置信息。
巧合的是,以上这俩问题,通过引入卷积这个技术方案可以【一石二鸟】。
下面举例推导,假设输入是k×l的单通道图像,准备使用的网络是含有一个隐层的多层感知机。
-
如果隐层为一般的全连接层:
容易写出隐层前向传播的公式:
h = u + ∑ i = 0 k l W i x i (1-1) h=u+\sum_{i=0}^{kl}W_ix_i\tag{1-1} h=u+i=0∑klWixi(1-1)
(1-1)中,kl分别为图像宽度和高度;x为把图像压成一维后的向量(1×kl);h为隐层一维表示向量(不妨先令其与x同大小,1×kl);u为同大小偏置;W是kl×kl大小的二维矩阵。此时的参数量为W矩阵的元素数,
kl^2。 -
如果隐层为完全卷积层:
这次我们要做出改进:不把图像看成一维的,以充分利用其隐含的空间信息,利用卷积核来利用这种空间信息,进行特征提取。
其中,这个“完全卷积”是指:用【若干】个大小为
s×s的卷积核,对原图做卷积。具体是多少个呢?取决于卷积核移动的步长。可以理解为:**在图像上每做一次卷积操作 就更换一个新的卷积核。**对应的隐层前向传播公式为:
H i , j = U i , j + ∑ a ∑ b W i , j , a , b X i + a , j + b (1-2) H_{i,j}=U_{i,j}+\sum_{a}\sum_{b}W_{i,j,a,b}X_{i+a,j+b}\tag{1-2} Hi,j=Ui,j+a∑b∑Wi,j,a,bXi+a,j+b(1-2)
(1-2)中,a、b分别为卷积的横向纵向步长。此时W是一个四维矩阵,大小为:s×s×(k2/a)×(l2/b)此时的参数量为:
(s/a)×(s/b)×kl^2。 -
如果隐层为卷积层:(就是我们现在常用的)
第二种方法利用了图像的重要特性之一 —— 局部性,但仍然存在参数量过大的问题(可以看到其参数量和全连接是一个级别的)。那这次我们的改进更加“极端”:
**对于单通道的输入图像,只用一个卷积核进行平移卷积操作;而且对于图像上的任一部分,只做一次卷积。**计算公式如下:
H i , j = U i , j + ∑ a ∑ b W a , b X i + a , j + b (1-3) H_{i,j}=U_{i,j}+\sum_{a}\sum_{b}W_{a,b}X_{i+a,j+b}\tag{1-3} Hi,j=Ui,j+a∑b∑Wa,bXi+a,j+b(1-3)
(1-3)中,W缩小为2维矩阵,大小为:s×s。(就是一个卷积核嘛)此时的参数量为:
s×s。
幸运的是,我们不仅通过第三种方法减少了参数量,同时还利用到了图像的另一个重要特性——平移不变性。
想象一下,在第二种方法中,给图像各个部分做卷积的卷积核都不一样,那图像左上角的猫咪和右下角的猫咪经过隐层后的表示一样吗?(假设两只猫咪一模一样,是平移过去的)
很明显不会一样。那经过第三种方法的隐层呢?那就是一模一样的了,这正是我们想要的。
最后解释一下卷积神经网络利用的两个图像特性(或者说假设):
1. 平移不变性:对于图像中完全相同的两个物体,其通过隐层后的表示不应因其所处位置改变而改变。
2. 局部性:图像的局部特征往往比全局特征更容易表示图像中的某个物体。
2. 卷积神经网络技术细节
相信你仔细看完上一节的内容后对卷积神经网络有了比较充分的认识。但想要卷积具体用在神经网络中,还需要引入全套技术细节。为了更好地使用、改进甚至创造卷积神经网络,我们需要进一步了解这些技术细节。
2.1 卷积在神经网络中是怎么运作的?
通过上一节的内容,对于单通道图像相信你已经足够了解卷积的运作了,为了更清晰的表示,这里通过图形来描述 一张单通道图像通过卷积层发生的事情:
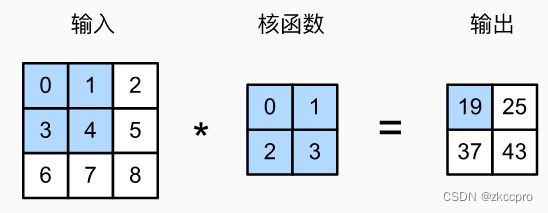
图1 单通道输入、单通道输出卷积层的运作方式
然鹅实际中,以上这种方式很少用到。我们的输入有时是三通道的RGB图像,而且我们更希望运用卷积层将输入数据进行【升维】操作,以提取到更多可能有用的潜在特征。
这就需要多通道输入、多通道输出的卷积层。这时的卷积层应该如何运作呢,一图胜千言,下图可以很好的说明:
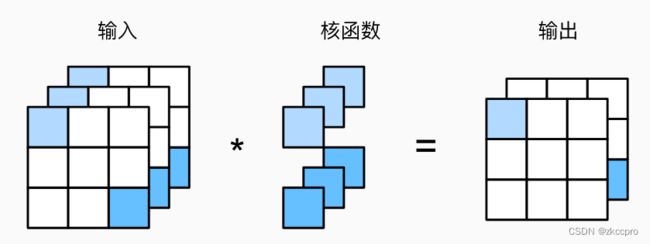
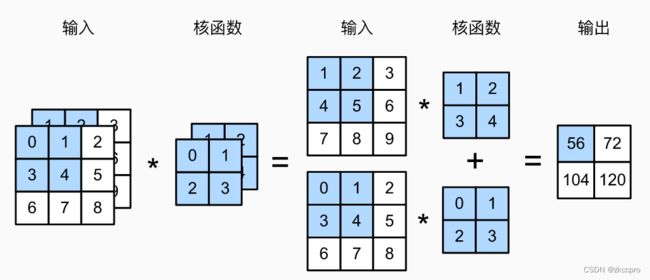
图2 多通道输入、多通道输出卷积层的运作方式
如图2(上),输入有3通道,输出有2通道。我们总共需要6个不同的卷积核对其进行卷积:上面3个卷积核分别卷积输入的3个通道,并把结果【相加】后作为输出的第1个通道;下面的3个卷积核分别卷积输入的3个通道,并把结果【相加】后作为输出的第2个通道。
到这里,你应该明白卷积神经网络对于多输入通道多输出通道的工作原理了。最重要的事情是计算任一卷积层所含的参数:(划重点,要考的…)
对于 m个输入通道、n个输出通道、卷积核大小为(s×s)的卷积层来说,其参数为:m×n×s×s。
pytorch对卷积操作有直接的接口支持:
conv = nn.Conv2d(input_channels, output_channels, kernel_size=3)
output = conv(input)
这就定义了一个卷积层,它是一个callable对象,好理解吧!
2.2 填充与步幅
-
如图3,经过卷积层后,输出图像的尺寸相比输入发生了缩小。有时尺寸缩小是我们不希望看到的,因为这就意味着每做一次卷积就丢失了一圈边缘像素。所以为了解决这个问题,我们需要引入padding(填充)来解决。
仔细观察图3,可以发现丢失边缘信息是右边一列和下面一行,因此填充时只需把这部分填上0即可。
pytorch对此有封装好的接口:
conv = nn.Conv2d(1, 1, kernel_size=(3, 3), padding=1) # 高度和宽度各填充1行/列 conv = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1)) # 高度和宽度各填充2和1可见,当卷积核大小不一样时,对应损失边缘行数(列数)也不一样,因此填充大小也不一样。
一般情况下,我们在做卷积时希望保持输入输出图像尺寸不变。
-
步幅:
如图4,如果卷积核移动的步幅大于1,输出图像尺寸将有更明显地缩小,直接减半了:
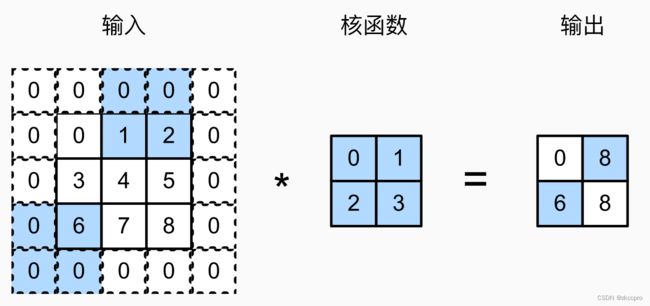
图4 步幅在卷积层中的作用类似,pytorch对步幅(stride)也有可直接调用的接口:
# 横纵向的步幅均为2 conv = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2) # 横向步幅为3,纵向步幅为4 conv = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))这个东西在卷积神经网络里不咋常用,它能做的事情下面的池化也可以,但比池化更灵活一些(相当于池化的策略是可学习的)。
2.3 池化(汇聚)
池化(汇聚)的作用和步幅不为1的卷积核类似,都可以起到缩小图像尺寸的作用。实际上**,池化层就是一个固定策略、卷积核大小和步幅均为n的卷积层。**
常见的池化策略有两个:最大池化、平均池化。
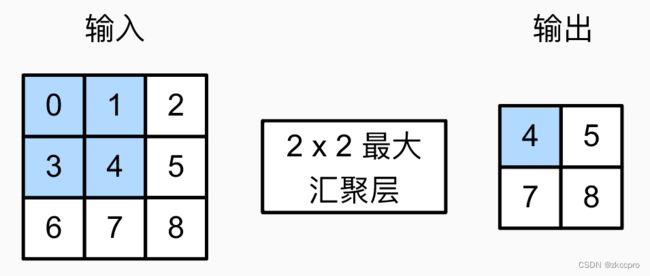
图5 最大池化层
图5可以很好地说明池化层的作用,图5的最大池化层做的事情就是:以2×2为卷积核大小,以1为步幅,以最大池化为固定策略,对原图做卷积,得到输出图像。平均池化也类似,好理解吧…
**池化层可以有效地起到过滤冗余信息的作用。**想象卷积神经网络就是一个过滤器,卷积层提取信息的同时也需要有滤网来过滤掉一些冗余信息,那么池化层就起到了这个过滤网的作用。他把输入层的具体元素去除掉,只保留局部的最大值或者平均值,在实际使用中这是十分有效的。
同样,pytorch对此也有接口支持:(pytorch默认池化卷积核尺寸与步幅相等)
import torch.nn.functional as F
# 若干卷积层...
x = nn.MaxPool2d(2) # 最大池化,卷积核大小为2,输出长宽都将缩小2倍
# 若干卷积层...
x = nn.AvgPool2d(4) # 平均池化,卷积核大小为4,输出长宽都将缩小4倍
# 全连接层...
上面的代码也透露了一个使用建议:一般来说,在网络中接近输入的位置尽量使用最大池化,网络中接近输出的位置尽量使用平均池化。因为明显最大池化将损失更多的信息,到了网络后面几层剩下的都是十分滴珍贵的信息,不应该将其滤掉。
另外,对于CV任务有一种说法是:最大池化可以提取图像细节纹理,平均池化容易提取图像背景。仔细想想也好理解吧…为啥不用最小池化呢?因为最小池化的输入可能都是0,对前向传播起到抑制作用。
2.4 特征映射与感受野
卷积层有时被称为特征映射(feature map),其实就是输入和输出之间的维度升降器。
而感受野是指:对于第n层卷积层输出图像中的某一个元素x,影响其计算的原输入图中所有像素,即为元素x的感受野(receptive field)。
感受野的概念可能不太直观,如果不太理解可以参考图1。在图1的输出中,标蓝的元素[19],其计算需要输入图像中标蓝的[0,1,3,4]元素。那么可以说,输入中的[0,1,3,4]是输出元素[19]的感受野。(当然,你应该合理外推,假设图1中的输入和输出之间还有若干层)
有时我们想要每个输出元素的感受野尽可能大(全局感受野),这就需要建立一个更深的网络,或者设计巧妙的跳跃连接来达到这个目的。
3. LeNet
最后,LeNet是每一个CVer都应该知道的网络,它是世界上第一个成功应用的卷积神经网络。LeNet在1998年被Yann LeCun提出,并以其名字命名。
LeNet当时就广泛应用于各个手写字识别领域,并取得了非常好的准确率,一度赶超当时人工智能领域的主流算法SVM。LeNet之后,卷积神经网络逐渐成为了CV的主流方法,同时也促使深度学习成为监督学习的主流方法。
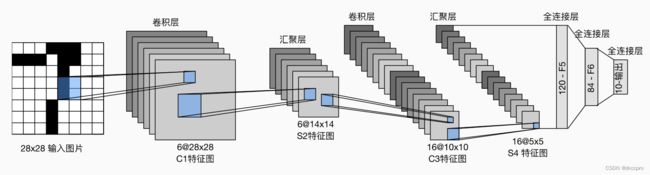
图6 LeNet结构
这就是LeNet的结构,也没多深,就。。。
一层卷积,一层池化;一层卷积,一层池化;全连接、全连接、全连接;over!
并不复杂的结构就能在手写字各种落地领域有极好的效果,可见卷积神经网络整套技术方案的合理性!
时至今日,你可以用各种深度学习框架快速搭建出LeNet,比如用pytorch:
import torch
from torch import nn
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
可见,现在的各种深度学习框架同样强大且易用,甚至逐渐形成了一套从模型设计到部署到落地推理的庞大生态。这对于今天深度学习领域研究的极块发展 起到了很大的推动作用。