《Reinforcement Learning: An Introduction》第5章笔记

Chapter 5 Monte Carlo Methods

Monte Carlo 方法不假设拥有完备的环境知识，它仅仅需要经验–从与环境的实际或模拟交互中得到的一系列的状态、动作、和奖励的样本序列。

Monte Carlo方法是基于平均采样回报的来解决强化学习问题的方法。

5.1 Monte Carlo Prediction

Monte Carlo 方法的基本思想：一个状态的价值是它的期望回报，也就是从那个状态开始能得到的期望的未来累积折扣奖励。因此一种简单的实现方法是将从访问到状态开始观察到的回报平均化。随着越来越多的回报被观察到，这个平均值肯定会收敛到期望值。

假设我们要估计在策略$\pi$下的状态s的价值$v_{\pi }(s)$，并且给定一个遵循策略$\pi$并且经过状态s的episodes集合。 将一个episode中状态s的每一次出现称为对s的一次访问(visit)。可想而知，在同一个episode里，状态s可能会被访问多次，我们将一个episode里状态s第一次被访问称为s的首次访问（first visit to s）。

• 首次访问MC方法（The first-visit MC method）将首次访问后的平均回报作为$v_{\pi }(s)$的估计。

• 每次访问MC方法（every-visit MC method）将其估计为所有访问 s 之后的平均回报。

• 首次访问MC方法和每次访问MC方法非常相似但有些许不同的理论性质。 当s的访问次数趋于无穷时，两者都可以收敛到$v_{\pi }(s)$。

下图是首次访问MC方法的流程图，每次访问MC方法除了去检查$S_t$是否已经出现过之外，是一样的。

【Example 5.1: Blackjack】 是一个用MC方法的例子。

Monte Carlo算法能用回溯图表示吗？当然可以，对于Monte Carlo 的估计值$v_{\pi }$， 状态节点是根节点，而它下面的是一个特定的单个序列的整个转移轨迹（以终止状态结束），如下图所示。

Monte Carlo 方法不是自举(bootstrap)的，它对于每个状态的估计是独立的。因为这个特点，当只想知道一个状态或一小部分状态的价值时，Monte Carlo方法就特别有吸引力；此时只需要从这些感兴趣的状态出发生成很多样本序列，并只对这些状态进行平均回报的计算。（这是Monte Carlo 方法的第三个优点，可以从实际经验学习，也可以从模拟经验学习是另外两个优点）

5.2 Monte Carlo Estimation of Action values

Monte Carlo 方法的最优目标之一是估计$q_{\ast }$，为了实现它，考虑对动作价值的策略评估问题。

对动作价值的策略评估问题是估计$q_{\pi }(s,a)$， 即遵循策略$\pi$，从状态s出发，采取动作a的期望回报。 Marlo Carlo方法估计动作价值的方法与上一节估计状态价值时是一样的。如果在状态s被访问，并且采取了动作a时，称状态-价值对在一个序列中被访问：

• 每次访问MC（every-visit MC）方法将所有动作-价值对得到的回报的平均值作为动作价值函数的近似。
• 首次访问MC（first-visit MC）方法将每个序列中第一次在这个状态下采取这个动作得到的回报的平均值作为动作价值函数的近似。

此时我们面临的唯一复杂情况是许多状态-价值对可能从来没有被访问过。当$\pi$是一个确定性策略，那么遵循$\pi$意味着在每个状态只会观测到一个状态的回报。当无法获取回报进行平均时，Monte Carlo将无法根据经验来改善其他动作的估计。所以与第2章讨论过k臂赌博机问题一样，这是如何保持探索(maintaining exploration)的普遍问题。解决这个问题的一个方法是：
​ exploring starts：使序列从一个指定的状态-价值对开始，同时保证所有状态-价值对都有一个非零概率被选择成起点。这个方法保证了，在采样序列的数目趋向无穷时，所有状态-价值对都会被访问无数次。

5.3 Monte Carlo Control

在第4章 提到过广义策略迭代GPI（generalized policy iteration，GPI），GPI同时维护一个近似的策略和近似的价值函数。价值函数不断迭代使其更精确地近似对应当前策略的价值函数，而策略也根据当前的价值函数不断调优，就如下图显示的那样，这两个过程最终会使策略和价值函数趋向最优解。

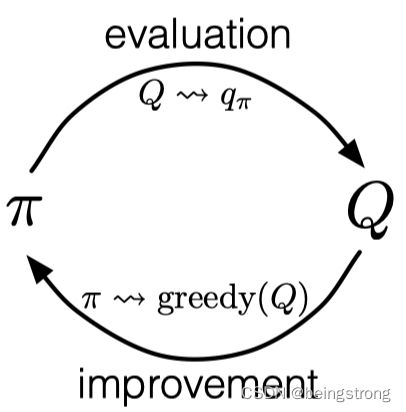
经典策略迭代的Monte Carlo 版本，从任意策略${\pi }_0$开始，交替完成策略迭代和策略提升，以最优策略和动作价值函数作为终止：
$${\pi }_0\stackrel{E}{⟶}{q}_{\pi 0}\stackrel{I}{⟶}{\pi }_1\stackrel{E}{⟶}{q}_{\pi 1}\stackrel{I}{⟶}{\pi }_2\stackrel{E}{⟶}\cdots \stackrel{I}{⟶}{\pi }_{\ast }\stackrel{E}{⟶}{q}_{\ast }$$
上式中的$\stackrel{E}{⟶}$是策略评估，$\stackrel{I}{⟶}$是策略提升。策略评估可以按照5.2节所述执行。如果基于两个假设：1. 序列是由探索性出发（exploring start）生成的；2. 进行策略评估时可以在无限多的序列中进行探索。Monte Carlo方法可以对任意${\pi }_k$ 精确的计算对应的$q_{{\pi }_k}$。
策略提升方法是在当前价值函数上贪心地选择动作。对于任意的动作价值函数q，对应的贪心策略为：对于任意的$s\in \mathcal{S}$，一定选择具有最大动作价值的动作：
$$\pi (s)\dot{=}\underset{a}{\mathrm{argmax}}q(s,a)(5.1)$$

策略提升能够通过将$q_{{\pi }_k}$的贪心策略作为${\pi }_{k+1}$ 来实现，这样的${\pi }_k$和${\pi }_{k+1}$满足4.2节的策略提升定理，对于所有状态$s\in \mathcal{S}$:
$$\begin{array}{rl}{q}_{{\pi }_k}(s,{\pi }_{k+1}(s))& =q_{{\pi }_k}(s,\underset{a}{\mathrm{argmax}}{q}_{{\pi }_k}(s,a))\\ & =\underset{a}{\max }{q}_{{\pi }_k}(s,a)\\ & \ge q_{{\pi }_k}(s,{\pi }_k(s))\\ & \ge v_{{\pi }_k}(s)\end{array}$$

在之前章节学到过，这个定理保证了${\pi }_{k+1}$ 一定比${\pi }_k$更优，除非${\pi }_k$已经是最优策略，这样两者都是最优策略。所以在只能得到若干个回合采样序列而不知道环境动态知识时， Marte Carlo方法就可以用来寻找最优策略。

前面我们提到作了两个假设来保证Marte Carlo方法的收敛，但是为了得到一个实际可用的算法，我们必须去除这两个假设，我们先考虑如何去掉第一个假设。

去掉第一个假设，即策略评估时可以在无限多的序列中进行探索，有两种方法（DP和Monte Carlo方法都适用）:

• 在每次策略评估中对$q_{{\pi }_k}$做出尽量好的逼近。这要求做一些假设并定义一些测度，来获取逼近误差的幅度和出现概率的上下界，然后采取足够多的步数来保证这些边界足够小。这个方法可以保证收敛到令人满意的近似水平，但是在实际使用中，即使问题足够小，也可能需要太多的序列用于计算。
• 不再要求在策略改进之前就完成策略评估。在每一个评估步骤中，我们让动作价值函数逼近$q_{{\pi }_k}$，但我们并不期望它在经过很多步之前非常接近真实的值。 在第4章中的价值迭代就是一种极端实现方式。

在每一个序列结束后，使用观测到的回报进行策略评估，并在该序列访问到的每一个状态上进行策略的改进，基于这个思路的算法，被称为Monte Carlo ES（Monte Carto with Exploring Starts），伪代码如下图：

5.4 Monte Carlo Control without Exploring Starts

如何避免很难被满足的探索性出发假设呢？唯一的一般性方法是保证agent能够持续地选择所有动作，有两种方法可以保证这一点，被称为在线策略（on-policy）方法和离线策略（off-policy）方法：

• 在线策略方法尝试评估和提升用来决策的策略。也就是用于生成采样数据序列的策略和用于实际决策的待评估和改进的策略是相同的。前文的Monte Carlo ES 方法是一个在线策略的例子。
• 离线策略方法评估和提升的策略不同于用来生成数据的策略。

本节讨论在线Monte Carlo 方法如何用来去除不实际的探索性出发假设。

在线策略控制方法的策略通常是soft的，也就是说对于对于所有$s\in \mathcal{S}$和$a\in \mathcal{A}(s)$，有$\pi (a|s)>0$，但它们会逐渐逼近到一个确定性策略。在线策略算法使用 $ϵ-greedy$策略，在大多数时候选择具有最大预估动作价值的动作，以一个小的概率$ϵ$ 来从所有动作中等概率的随机选择一个动作。也就意味着所有非贪心动作有一个最小概率$\frac{ϵ}{|\mathcal{A}(s)|}$被选中，而贪心动作有概率$1-ϵ+\frac{ϵ}{|\mathcal{A}(s)|}$。$ϵ-greedy$策略是$ϵ-soft$策略的一个例子，即对某个$ϵ>0$，对于所有状态和动作满足$\pi (a|s)\ge \frac{ϵ}{|\mathcal{A}(s)|}$。

在线策略的首次访问MC控制算法的伪代码如下图，对于任意的$ϵ-soft$策略$\pi$，根据$q_{\pi }$生成的任意一个$ϵ-greedy$策略保证优于或等于$\pi$。

根据策略提升定理，对于任意$ϵ-soft$策略$\pi$，任意根据 $q_{\pi }$生成的$ϵ-greedy$策略都是对其的提升。假设${\pi }^{\prime }$是一个$ϵ-greedy$策略， 策略提升定理的条件成立，因为对于任意的状态$s\in \mathcal{S}$：
$$\begin{array}{rl}{q}_{\pi }(s,{\pi }^{\prime }(s))& =\sum _a{\pi }^{\prime }(a|s)q_{\pi }(s,a)\\ & =\frac{ϵ}{|\mathcal{A}(s)|}\sum _a{q}_{\pi }(s,a)+(1-ϵ)\underset{a}{\max }{q}_{\pi }(s,a)(5.2)\\ & \ge \frac{ϵ}{|\mathcal{A}(s)|}\sum _a{q}_{\pi }(s,a)+(1-ϵ)\sum _a\frac{\pi (a|s)-\frac{ϵ}{|\mathcal{A}(s)|}}{(1-ϵ)}{q}_{\pi }(s,a)\\ & (thesumisaweightedaveragewithnonnegativeweightssummingto1,andassuchitmustbelessthanorequaltothelargestnumberaveraged)\\ & =\frac{ϵ}{|\mathcal{A}(s)|}\sum _a{q}_{\pi }(s,a)-\frac{ϵ}{|\mathcal{A}(s)|}\sum _a{q}_{\pi }(s,a)+\sum _a\pi (a|s)q_{\pi }(s,a)\\ & =v_{\pi }(s)\end{array}$$

​ 所以，通过策略提升定理，有${\pi }^{\prime }\ge \pi$，也就是对于所有状态$s\in \mathcal{S}$，有$v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s)$，而该式等号成立的条件是：当且仅当${\pi }^{\prime }$和$\pi$都是最优的$ϵ-soft$策略，也就是它们比所有其他的$ϵ-soft$策略都更优或相同（证明略，见原书）。

5.5 Off-policy Prediction via Importance Sampling

所有的学习控制算法有一个困境：它们希望学习到的动作可以使随后的智能体行为是最优的，但是为了探索所有的动作，以保证找到最优动作，它们需要采取非最优的行动。那怎么解决这个困境呢？ 离线策略（off-policy）的解决办法是使用两个策略，一个策略用来学习并成为最优策略，被称为目标策略(target policy)；另一个策略做更多探索，用来产生智能体的行动样本，被称为行为策略(behavior policy)。这种情况下认为学习所用的数据“off"了目标策略，因此整个过程被称为离线策略学习。

在线策略和离线策略的对比：

• 在线策略通常更简单，且首先被考虑。
• 离线策略需要额外的概念和记号。并且因为其数据来自一个不同的策略，所以离线策略方法方差更大，收敛更慢。
• 但是离线策略更强大更通用，可以将在线策略看做是目标策略和行为策略是相同的离线策略方法的特例。

假设将目标策略记为$\pi$， 行为策略记为$b$，两个策略是已知且固定。

覆盖假设(assumption of coverage)： 为了使用从$b$得到的序列来估计$\pi$，我们要求在$\pi$下采取的每个动作都至少偶尔能在$b$下发生，也就是说当$\pi (a|s)>0$时，要求$b(a|s)>0$。 在这个假设下，在与$\pi$不同的状态下，$b$必须是随机的。而目标策略$\pi$可能是确定的。

几乎所有的离线策略都使用重要性采样（importance sampling），一种给定来自其他分布的样本的条件下，来估计某种分布的期望值的通用技术。

重要度采样比(importance-sampling ratio)：轨迹在目标策略和行为策略中出现的相对概率。离线策略学习将回报用重要度采样比来加权的方式来应用重要性采样。给定起始状态$S_t$，后续的状态-价值轨迹$A_t,S_{t+1},A_{t+1},\cdots ,S_T$在策略$\pi$下发生的概率是：
$$\begin{array}{rl}& Pr\{A_t,S_{t+1},A_{t+1},\cdots ,S_T|S_t,A_{t:T-1}\sim \pi \}\\ & =\pi (A_t|S_t)p(S_{t+1}|S_t,A_t)\pi (A_{t+1}|S_{t+1})\cdots p(S_T|S_{T-1},A_{T-1})\\ & =\prod _{k=t}^{T-1}\pi (A_k|S_t)p(S_{k+1}|S_k,A_k)\end{array}$$
式中的$p$是第3章中的式(3.4)定义过的状态转移概率，因此在目标策略和行为策略下的轨迹的相对概率（重要度采样比）为：
$${\rho }_{t:T-1}\dot{=}\frac{{\prod }_{k=t}^{T-1}\pi (A_k|S_t)p(S_{k+1}|S_k,A_k)}{{\prod }_{k=t}^{T-1}b(A_k|S_t)p(S_{k+1}|S_k,A_k)}=\prod _{k=t}^{T-1}\frac{\pi (A_k|S_t)}{b(A_k|S_t)}(5.3)$$
尽管整体轨迹的概率值依赖于MDP的状态转移概率，并且MDP的状态转移概率通常是不可知的，但是它们在分子和分母中是完全相同的，所以可被约分。重要度采样比最终仅依赖于两个策略及其数据，而不依赖于MDP。

我们希望估计目标策略下的期望回报（价值），但是我们只有从行为策略得到的回报$G_t$，这些从行为策略得到的回报有错误的期望$\mathbb{E}[G_t|S_t=s]=v_b(s)$，所以不能用它们的平均来得到$v_{\pi }$。解决方法是使用重要性采样，使用重要度采样比${\rho }_{t:T-1}$可以调整回报使其有正确的期望值：
$$\mathbb{E}[{\rho }_{t:T-1}{G}_t|S_t=s]=v_{\pi }(s)(5.4)$$

介绍完基础概念后，终于到了本节算法出场的时候了，也就是平均化一批遵循策略$b$的观测序列的回报来估计$v_{\pi }(s)$的Monte Carlo 算法。对于每次访问MC方法，定义所有访问过的状态s的时刻集合为$\mathcal{T}(s)$； 对于首次访问MC方法，$\mathcal{T}(s)$只包含在序列内首次访问状态s的时刻。用$T(t)$表示时刻t后的首次终止，$G_t$表示在t之后到达$T(t)$的回报。则$\{G_t{\}}_{t\in \mathcal{T}(s)}$是状态s对应的回报值，而$\{{\rho }_{t:T(t)-1}{\}}_{t\in \mathcal{T}(s)}$ 是对应的重要度采样比，为了估计$v_{\pi }(s)$，有两种方法：

• 普通重要性采样(ordinary importance sampling)： 根据重要度采样比来调整回报值并对结果进行平均：
  $$V(s)\dot{=}\frac{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}{G}_t}{|\mathcal{T}(s)|}(5.5)$$
• 加权重要性采样(weighted importance sampling)：根据重要度采样比来调整回报值并对结果进行加权平均，式中如果分母为零，则值也为零:

$$V(s)\dot{=}\frac{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}{G}_t}{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}}(5.6)$$

那这两种重要度采样方法有什么区别呢？

• 对于首次访问MC方法，普通重要性采样是无偏的，加权重要性采样是有偏的
• 对于首次访问MC方法，普通重要性采样的方差一般是无界的，而如果假设回报有界，即使重要性采样比是无界的，加权重要性采样的方差也能收敛到零。
• 在实际应用中，加权重要性采样因为低方差被偏好使用，但是普通重要性采样因为更容易扩展到本书后面的函数逼近的近似方法也不会被放弃使用。
• 在每次访问MC方法中，两种重要性采样方法都是有偏的，但是随着样本数增加，偏差会逐渐趋近于0。

实际使用中，每次访问MC方法更常被使用，因为它不需要跟踪状态是否被访问过，并且更容易扩展到近似。使用加权重要性采样的用于off-policy的策略评估的完整版每次访问MC算法在下一节5.6节会学到。

5.6 Incremental Implementation

在第2章的2.4节学过的增量式实现可以直接应用到Monte Carlo方法，在那里是计算平均奖励，在Monte Carlo方法中我们计算平均回报。对于在线策略Monte Carlo方法可以直接使用已经学过的增量式实现方法，而对于离线策略Monte Carlo方法，需要分别讨论一下普通重要性采样和加权重要性采样。

普通重要性采样方法，可以直接使用第2章的增量式方法，只是将奖励替换成缩放后的回报就可以了。

加权重要性采样方法，因为需要对回报加权平均，就需要一个略微不同的增量式算法。

假设有一个回报序列$G_1,G_2,\cdots ,G_{n-1}$，都从相同的状态开始，并且每一个回报都对应一个随机权重$W_i$（例如，$W_i={\rho }_{t_i:T(t_i)-1})$。希望得到如下估计，并且在获得了一个额外的回报值$G_n$时能保持更新：
$$V_n\dot{=}\frac{{\sum }_{k=1}^{n-1}{W}_k{C}_k}{{\sum }_{k=1}^{n-1}{W}_k},n\ge 2(5.7)$$

为了能不断跟踪$V_n$的变化，必须为每一个状态维护前n个回报对应的权值的累加值和$C_n$， $V_n$的更新规则为：
$$\begin{gathered} V_{n+1}\dot{=}{V}_n+\frac{W_n}{C_n}[G_n-V_n],n\ge 1(5.8) \\ and{C}_{n+1}\dot{=}{C}_n+W_{n+1},C_0\dot{=}0 \end{gathered}$$

下图是一个完整的Monte Carlo 策略评估的增量式算法，虽然命名为离线策略场景，并使用加权重要性采样，但是可以适用于在线策略场景（通过使目标和行为策略一样，并且W总是为1）。

5.7 Off-policy Monte Carlo Control

下图是离线Monte Carlo控制算法的伪代码，使用行为策略生成数据，学习和提升目标网络。为了探索所有的可能性，要求行为策略一定是的soft的。

这个方法一个潜在的问题是，当回合中的所有其余动作都是贪心的，此方法只能从回合的尾部学习。如果非贪心的行为很普遍，那么学习将会很慢，尤其是对长回合早期出现的状态，这可能会大大减慢学习速度。解决这个问题的最重要方法可能是结合下一章会学到的时间差分学习。如果$\gamma$小于1，下一节提出的想法可能也有很大帮助。

5.8 *Discounting-aware Importance Sampling

TODO，后面再看

5.9 *Per-decision Importance Sampling

TODO，后面再看

5.10 Summary

关键知识点

• Monte Carlo 方法的三个优点
• Monte Carlo 方法的第四个优点：不符合马尔科夫性时损害较小，因为它们不是自举的(boostrap)
• 探索式出发
• 在线策略(on-policy)算法
• 离线策略(off-policy)算法
• 重要性采样、普通重要性采样、加权重要性采样

---

参考资料

1. 《Reinforcement Learning: An Introduction》Sutton, Richard S. and Andrew G. Barto. 第2版， 书籍网站
2. https://github.com/ShangtongZhang/reinforcement-learning-an-introduction
3. https://github.com/YunlianMoon/reinforcement-learning-an-introduction-2nd-edition/tree/master