《Reinforcement Learning: An Introduction》第2章笔记

2. Multi-armed Bandits

• 评估性反馈（evaluative feedback） 完全取决于采取的动作，这是强化学习采用的方式。纯粹的评估性反馈表明要执行的动作有多好，但是不关注它是否是可能的最好或最坏的动作。
• 指导性反馈（instructive feedback）独立于要采取的动作，这是监督学习的基础。纯粹的指导性反馈表明要采取的正确动作，独立于实际上采取的动作。

本章在只有一个动作的简化情况讨论强化学习的评估性质，也就是所谓的非关联(nonassociative)情形，避免了完全强化学习问题的许多复杂情况。

这个特别的非关联的，评价性反馈问题是“k臂赌博机问题( k-armed Bandit Problem)”的简化版本。

2.1 A k-armed Bandit Problem

k臂赌博机问题： 假设你要重复地从k个选项或动作中进行选择，每次选择后你都将收到一个数值奖励，这个奖励服从一个取决于你选择的动作的平稳概率分布。你的目标是在一段时间段内最大化期望得到的总奖励，比如1000次选择或1000个时间步。

在k臂赌博机问题中，选择k个动作中的每一个都会有一个期望的或者平均的奖励，将它称为该动作的“价值（value)”。 设在时刻 $t$ 选择的动作为$A_t$， 对应的奖励为$R_t$， 任一动作$a$ 的价值记作 $q_{\ast }(a)$， 即$a$被选择后的期望奖励为：

$$q_{\ast }(a)\dot{=}\mathbb{E}\left[R_t\mid A_t=a\right]$$

如果我们可以知道每个动作的价值，那解决k臂赌博机问题就很简单，只要选择具有最大价值的动作就可以了。当我们不能确切的知道每个动作的价值，我们可以通过估计的方式来得到它，将时刻$t$ 估计的动作$a$的价值记作 $Q_t(a)$， 我们希望它能够接近$q_{\ast }(a)$。

贪心(greedy)动作 是指每一个时刻里估计的价值最高的那些动作，如果每次选择动作时，我们都选择贪心动作，此时就是利用(exploiting)， 如果选择那些非贪心的动作，此时就是在探索(exploring)。

2.2 Action-value Methods

动作价值方法(action-value methods)是指一类估计动作的价值并使用该估计来进行动作选择决策的方法。

在前面提到动作的真实值是该动作被选择的期望奖励，那一种很自然的估计价值的方法就是将实际收到的奖励进行平均：
$$Q_t(a)\dot{=}\frac{sumofrewardswhenatakenpriortot}{numberoftimesatakenpriortot}=\frac{{\sum }_{i=1}^{t-1}{R}_i\cdot 1_{A_i=a}}{{\sum }_{i=1}^{t-1}{1}_{A_i=a}}(2.1)$$
上式中$1_{predicate}$ 是指当$predicate$ 为$true$ 时随机变量为1，反之为0。当分母为0时，给$Q_t(a)$指定值，比如0，当分母趋向于无穷大时，根据大数定律，$Q_t(a)$将会收敛到$q_{\ast }(a)$。 这个估计动作价值的方法被称为“采样平均方法(sample-average)”。

最简单的动作选择方法是选择具有最高价值的动作（如果有多个，任意选择一个），也就是选择2.1节中定义的贪心动作，将这种贪心(greedy)动作选择方法记作：
$$A_t\dot{=}argma{x}_a{Q}_t(a)(2.2)$$
上式中的$argma{x}_a$ 是使得$Q_t(a)$值最大的动作。

贪心动作选择总是利用当前知识来最大化即时奖励，它根本不会花时间去采样次优的动作来看看它们是否可能会更好。一种简单的替换方法是 $ϵ-greedy$方法，它以一个小的概率$ϵ$ 来从所有动作中等概率的随机选择一个动作，其余时候按照贪心方法来选择动作。$ϵ-greedy$方法的优点是，如果时刻可以无限长，可以保证所有$Q_t(a)$收敛到$q_{\ast }(a)$， 最优动作的概率将会收敛到大于$1-ϵ$。

2.3 The 10-armed Testbed

为了评估贪心和$ϵ-greedy$ 动作价值方法，在测试平台上进行了定量比较。

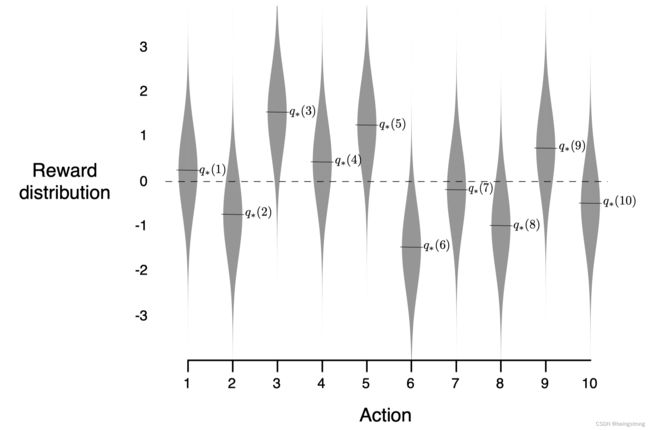
假设有k=10的2000个随机生成的k臂赌博机问题，对于每一个赌博机问题，动作的价值$q_{\ast }(a)$从一个均值为0方差为1的标准正态（高斯）分布中选择。对应于该问题的一个学习问题，在时刻$t$的实际奖励$R_t$ 从一个均值为$q_{\ast }(A_t)$ 方差为1的正态分布中选择。这些分布的示意如下图所示，将这一系列测试任务称为“10臂赌博机测试平台（10-armed Testbed）"。

对于每一个学习方法，我们将其在任一个赌博机上的1000次交互当做一轮试验，测量它的性能和动作。 我们进行2000次 独立试验，每一次在不同的赌博机问题上进行，以此来得到学习算法的平均表现。

上图是贪心方法与两种$ϵ-greedy$ 方法（$ϵ=0.01$ 和 $ϵ=0.1$）的比较，所有方法都用采样平均策略来做动作价值的估计：

• 图的上部分显示期望的奖励随着经验的增长而增长，贪心的方法在最初增长略微快一些，但是后面稳定在较低水平，从长远看，贪心的方法表现更糟，因为它经常陷入执行次优动作的怪圈。
• 图的下部分显示贪心方法大约只在三分之一的任务中找到最优动作。
• $ϵ-greedy$ 方法最终表现更好；$ϵ=0.1$ 的方法探索更多，通常更早发现最优动作，但是在每个时刻选择最优动作的概率却永远不会超过91%。$ϵ=0.01$的方法改善的更慢，但在图中的两种测度下，最终的性能表现都会比$ϵ=0.1$ 的方法更好。
• 所以为了充分利用高和低的$ϵ$ 值的优势，随着时间的推移来逐渐减少$ϵ$ 是不错的尝试。

但也要注意的是，$ϵ-greedy$ 方法相对贪心方法的优点依赖于任务。比如，假设奖励的方差更大，为10而不是1，由于奖励的噪声，它需要更多的探索，$ϵ-greedy$ 方法肯定比相比于贪心方法更好。但是如果奖励的方差为0，那么贪心方法只需要尝试一次就可以知道每个动作的真实价值，在这种情况下贪心方法会更好，因为它很快就可以找到最佳动作。 但是如果我们弱化一些其他的假设，在确定性场景下探索也是有优势的，比如非平稳性赌博机问题，总之强化学习需要考虑探索和利用的平衡。

2.4 Incremental Implementation

前面讨论的动作价值估计是对观测到的奖励进行采样平均，那么如何去高效计算这些均值呢？

为了简化标记，我们来讨论单个动作。设$R_i$ 是一个动作在第$i$次被选择后收到的奖励， 设$Q_n$ 是在它已经被选择了$n-1$ 次后的估计价值，可以由下式计算：
$$Q_n\dot{=}=\frac{R_1+R_2+\cdots +R_{n-1}}{n-1}$$
最直接的根据该公式计算的话，需要维护所有奖励的记录，这样内存和计算会随着时间的推移而增加，每一次新增的奖励都需要额外的内存来存储它，并且需要对分子进行额外的求和计算。

那么有办法去优化这个计算吗？答案是肯定的，为了计算每个新的奖励，很容易使用增量式公式来以小而恒定的计算来更新均值。给定$Q_n$ 和第 $n$ 个奖励值$R_n$ , 那么所有$n$ 个奖励的新的均值可由下式计算：
$$\begin{array}{rl}{Q}_{n+1}& =\frac{1}{n}\sum _{i=1}^n{R}_i\\ & =\frac{1}{n}\left(R_n+\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)\frac{1}{n-1}\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)Q_n\right)\\ & =\frac{1}{n}\left(R_n+n{Q}_n-Q_n\right)\\ & =\left(Q_n+\frac{1}{n}(R_n-Q_n)\right)(2.3)\end{array}$$
这个式子对于$n=1$ 也是成立的，对于任意$Q_1$，有$Q_2=R_1$， 对于每一个新的奖励，这个实现只需要内存存储$Q_n$ 和$n$， 以及少量的计算。

式2.3的更新规则在本书中经常出现，其一般形式是：
$$NewEstimate\leftarrow OldEstimate+StepSize\left[Target-OldEstimate\right](2.4)$$
上式中的表达式$[Target-OldEstimate]$ 是估计值的误差，它随着向”target"靠近的每一步而减少。尽管”target"可能存在噪声，我们还是假定它指明了可行的前进方向。

在式2.3中的步长(StepSize)参数：$\frac{1}{n}$会随着时间而改变，在本书中将步长参数记作 $\alpha$，或更一般的形式 ${\alpha }_t(a)$。

一个使用增量式计算的采样平均及$ϵ-greedy$ 方法的赌博机的伪代码如下， 假设函数$bandit(a)$ 接受一个动作并返回对应的奖励值。

2.5 Tracking a Nonstationary Problem

前面讨论的平均方法适用于平稳的赌博机问题，即收益的概率分布不会随着时间而改变。而实际上我们碰到的强化学习问题都是非平稳的(Nonstationary)，这种情况下对于近期的奖励相比于过去的奖励赋予更多的权重是合理的，流行的处理方法是使用固定步长参数，也就是将前面提到的增量式更新规则2.3式修改为：
$$Q_{n+1}\dot{=}{Q}_n+\alpha \left[R_n-Q_n\right](2.5)$$
式中的步长参数$\alpha \in (0,1]$ 是固定的。 这使得$Q_{n+1}$ 是过去奖励和初始估计$Q_1$ 的加权平均：

$$\begin{array}{rl}{Q}_{n+1}& =Q_n+\alpha \left[R_n-Q_n\right]\\ & =\alpha R_n+(1-\alpha )Q_n\\ & =\alpha R_n+(1-\alpha )(\alpha R_{n-1}+(1-\alpha )Q_{n-1})\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2{Q}_{n-1}\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2{R}_{n-2}+\\ & \cdots (1-\alpha {)}^{n-1}\alpha R_1+(1-\alpha {)}^n{Q}_1\\ & =(1-\alpha {)}^n{Q}_1+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}{R}_i(2.6)\end{array}$$

上式被称为加权平均是因为 $(1-\alpha {)}^n+{\sum }_{i=1}^n\alpha (1-\alpha {)}^{n-i}=1$， 由于权重随着 $1-\alpha$ 的指数衰减，这个方法有时候也被称作“指数近因加权平均（exponential recency-weighted average)"。

随机逼近理论中一个著名结果给出了保证收敛概率为1所需的条件：
$$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty and\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty (2.7)$$
第一个条件是为了保证步长足够大，最终能够克服任何初始条件或随机波动。 第二个条件保证最终步长足够小以保证收敛。

对于采样平均场景：${\alpha }_n(a)=\frac{1}{n}$ 下两个条件都满足，而对于固定步长参数:${\alpha }_n(a)=\alpha$ 的第二个条件不满足，说明估计永远无法完全收敛，而是会随着最近得到的奖励而变化，而这是在非平稳环境中我们想要的，并且强化学习的问题通常是非平稳的。此外，符合式2.7的步长序列参数序列常常收敛的很慢，或者需要大量调试才能得到一个满意的收敛率。

2.6 Optimistic Initial Values

前面讨论的所有方法都某种程度上依赖于初始动作价值估计$Q_1(a)$，在统计语境里，这些方法都是对初始估计有偏的(biased)。对于采样平均方法，当所有动作都至少被选择一次后，偏差就消失了。而对于使用固定步长$\alpha$ 的方法，如式2.6所示的，偏差是一直存在的，虽然会随着时间的增加而减小。

在实践中，这类偏差不是问题，有时甚至是有用的。坏处是初始估计值如果不设置为0的话，就变成了必须由用户选择的一系列参数。好处是通过它们可以简单地设置期望奖励水平的先验知识。

初始动作价值同时可作为一种鼓励探索的简单方法。比如在前面的10臂赌博机试验中，将初始动作价值设置为$+5$（而不是0）。因为这个问题的$q_{\ast }(a)$是从均值为0方差为1的正态分布选择的， 那么动作价值初始值$+5$是一个过度乐观的值，但这个乐观会鼓励动作-价值方法去探索。

下图是在10臂赌博机测试平台上，将所有的$a$ 设置为$Q_1(a)=+5$ 的贪心方法，与$Q_1(a)=0$的$ϵ-greedy$ 方法的对比。在开始时，乐观初始化方法表现的更糟，因为它需要更多的探索，但是随着探索的变少最终将表现的更好。 所以将这种鼓励探索的技巧称作”乐观初始价值(optimistic initial values)"。

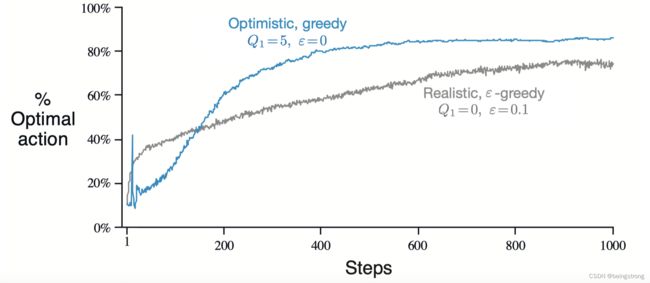
要注意的是乐观初始价值方法并不是鼓励探索的一般方法，在非平稳问题上就不适用。

2.7 Upper-Confidence-Bound Action Selection

当对动作-价值估计存在不确定性时，探索是必要的。$ϵ-greedy$ 方法强制非贪心动作被尝试，但是对于所有动作是一视同仁的。更好的方法是根据非贪心动作实际是最优动作的潜力来选择具体动作，同时考虑它们的估计值有多接近最大值以及这些估计的不确定性，一个有效的方法是根据下式来选择动作：
$$A_t\dot{=}argma{x}_a\left[Q_t(a)+c\sqrt{\frac{lnt}{N_t(a)}}\right](2.10)$$
上式中$lnt$是$t$的自然对数，$N_t(a)$是式2.1中的分母，也就是说动作$a$在时刻$t$之前被选择了多少次，而数字$c>0$控制探索的程度，当$N_t(a)=0$时，$a$就是满足最大化条件的动作。

这种置信度上界(upper confidence bound, UCB)的动作选择的思想是平方根项是对动作$a$的价值估计的不确定性或方差的度量。所以，最大值的大小是动作a的可能真实价值的上限，c决定了置信度。因为$N_t(a)$在分母上，每一次a被选择，不确定性就减小了，另一方面每次选择a之外的其他动作，分子上的$t$增加，而$N_t(a)$没有增加，不确定性估计就增加了。使用自然对数表明随着时间的推移，增加会越来越小，但它是无限的。所有动作最终都将被选中，但是低价值估计的动作或被频繁选择的动作，随着时间的推移被选择的频率会逐渐降低。

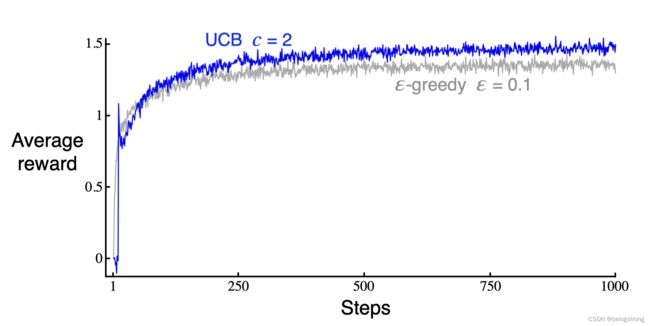
在10臂赌博机测试平台上的UCB的结果如下图，它通常表现更好，但是相比于$ϵ-greedy$ 方法更难推广到除赌博机外的其他强化学习问题，一个困难是在处理非平稳问题时，它需要比2.5节中介绍的更复杂的方法。另一个困难是要处理大的状态空间。

2.8 Gradient Bandit Algorithm

在这一节中考虑对每一个动作$a$学习一个数值偏好(preferences)，记作$H_t(a)\in \mathbb{R}$。 这个偏好越大，则这个动作就被越多的选择，但是这个偏好对于奖励项是没有任何说明性的。只有一个动作对于其他动作的相对偏好是重要的，如果我们将所有的动作偏好都加上1000对于动作概率是没有任何影响的，动作概率可由soft-max distribution (i.e., Gibbs or Boltzmann distribution)来决定：
$$Pr\{A_t=a\}\dot{=}\frac{e^{H_t(a)}}{{\sum }_{b=1}^k{e}^{H_t(b)}}\dot{=}{\pi }_t(a)(2.11)$$
上式中的${\pi }_t(a)$是在时刻t选择动作a的概率。所有动作的动作偏好值的初始值都是一样的（比如$H_1(a)=0,\forall a$），所以每个动作被选择的概率是相同的。

基于随机梯度上升的思想，对于softmax动作偏好有学习算法：在每一个步骤，当选择了动作$A_t$ 并收到了奖励$R_t$后，动作偏好可按如下来更新：
$$\begin{gathered} H_{t+1}(A_t)\dot{=}{H}_t(A_t)+\alpha (R_t-{\overline{R}}_t)(1-{\pi }_t(A_t)), \\ and{H}_{t+1}(a)\dot{=}{H}_t(a)-\alpha (R_t-{\overline{R}}_t){\pi }_t(a),foralla\ne A_t(2.12) \end{gathered}$$
式中的$\alpha >0$是步长参数， ${\overline{R}}_t\in \mathbb{R}$是不包括时刻t的累积回报的平均值（${\overline{R}}_t\dot{=}{R}_1$）， ${\overline{R}}_t$ 被作为奖励比较的基准值，如果奖励大于它，那么在将来选择$A_t$的概率增加，反之则减少。而未被选择的动作移动的方向是相反的。

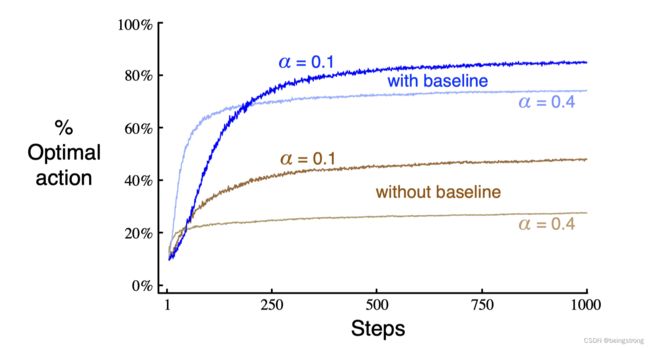
下图展示了梯度赌博机算法在真实期望奖励是从均值为$+4$的正态分布生成的变体10臂赌博机测试平台的结果。因为奖励基准项的存在，这个对所有奖励的变化不会影响梯度赌博机算法，因为它可以很快适应到新的水平。但是如果将基准项去掉，也就是将式2.12中的 ${\overline{R}}_t$ 设为0，那么性能将会显著降低。

2.9 Associative Search (Contextual Bandits)

关联搜索（associative search）任务的名称源于它既包含使用试错（trial-and-error）学习去搜索(search)最佳动作，又将这些动作和它们表现最佳的场景关联(association)起来。关联搜索在文献中一般被称作上下文赌博机(contextual bandits)。

关联搜索的例子：假设有一系列不同的k臂赌博机任务，每一步你都要随机地面对其中的一个，也就是说赌博机任务在每一步都是随机变化的。如果每一个赌博机任务被挑选给你时，你都会收到一些关于这些赌博机身份的明显线索（不是它的动作价值），比如随着赌博机改变，你看到的赌博机的颜色也改变。此时你可以学习策略来关联每个任务，用你看到的颜色作为信号，将每个任务和该任务下最优的动作关联起来，比如红色时，选择动作1，绿色时选择动作2。

关联搜索是介于k臂赌博机问题和完全强化学习之间的任务，它像完全强化学习一样涉及到学习一个策略，也像k臂赌博机问题一样每个动作只影响即时奖励。当允许一个动作影响到下一个时刻的情境和奖励，我们面对的就是完全强化学习问题了，是本书后面要讨论的问题了。

2.10 Summary

本章介绍了几种平衡探索和利用的方法：

• $ϵ-greedy$ 方法在一小段时间内进行动作的随机选择。
• UCB方法采用确定性的动作选择，但是通过在每个时刻对那些具有较少样本的动作进行优先选择来实现探索。
• 梯度赌博机算法不估计动作价值而是动作偏好，并且使用softmax分布来以分级的、概率式的方法来选择最优动作。
• 将贪心方法的初始值估计进行乐观的设置，也可以让贪心方法探索更多。

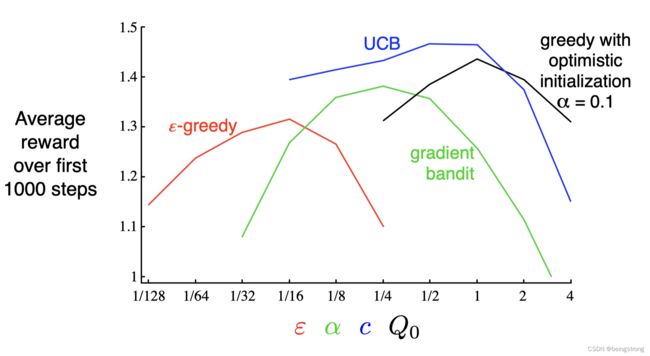
那么这些方法有没有哪个更好呢？使用如下的在10臂赌博机测试平台上得到的参数研究图(parameter study)来比较 ，图中的每条算法性能曲线都被看做是自己参数的函数，显示在单一尺度的x轴上。注意x轴上参数值的是以2的倍数变化的，并用对数坐标表示。 图中每个算法性能曲线都呈倒U型，都是在中间参数时表现最好。当我们评估一种方法时，不仅要看它在最佳参数设置上的表现，也要考虑它对参数值是否敏感，从图可以看出所有的算法对参数都不太敏感。在10臂赌博机问题上，UCB看起来是表现最好的。

---

参考资料

1. 《Reinforcement Learning: An Introduction》Sutton, Richard S. and Andrew G. Barto. 第2版， 书籍网站， 笔记中的全部图片都来源于书籍。
2. https://github.com/ShangtongZhang/reinforcement-learning-an-introduction
3. https://github.com/YunlianMoon/reinforcement-learning-an-introduction-2nd-edition/tree/master