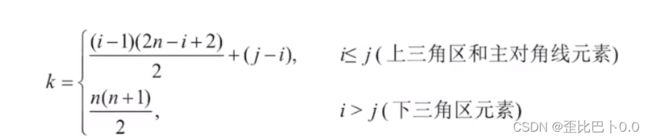特殊矩阵的压缩存储（详细版 通俗易懂 含c语言稀疏矩阵十字链表代码 ）

前言

此文章是本人第一篇博客，目的在于巩固过去所学的知识，同时可能会给大家带来一丝丝帮助，但由于没有经验加上本人能力极其有限，文章中可能存在不足之处，还请读者能够指正（`･ω･´）。

这篇文章首先会介绍矩阵压缩存储和特殊矩阵的基本概念，然后将会比较详细地说明几种特殊的矩阵：对称矩阵、三角矩阵、带状矩阵（三对角矩阵）、稀疏矩阵的压缩存储的策略，包括定量计算和十字链表的c语言代码和效果图，让我们开始吧！

注意，本文所用数组下标均为从0开始

正文

一.基本概念

压缩存储

在一个矩阵中，若多个数据的值相同，为了节省内存空间，则只分配一个元素值的空间，且零元素不占存储空间

特殊矩阵

可不是所有的矩阵都适合压缩存储！比如下面这个

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

下面介绍的几个特殊矩阵，才是将要重点介绍的对象：

1.对称矩阵

对称矩阵是指元素以主对角线为对称轴对应相等的n阶矩阵，即aᵢ,ⱼ=aⱼ,ᵢ  

比如

5	1	2	3	4
1	5	6	7	8
2	6	5	9	10
3	7	9	5	12
4	8	10	12	5

2.三角矩阵

三角矩阵是方阵的一种，分为上三角矩阵和下三角矩阵，上三角矩阵是指下三角区所有元素均为同一常量，下三角矩阵是指上三角区所有元素均为同一常量

上三角矩阵 下三角矩阵

 3.带状矩阵（三对角矩阵）

带状矩阵指所有非零元素都集中在以主对角线为中心的3条对角线的区域，其他区域均为零的矩阵特点：当|i-j|>1时，有aᵢ,ⱼ=0  或者说主对角线的相邻的上下左右元素可以是非0元素，再往外肯定是0元素的矩阵

如下图所示：

带状矩阵

4.稀疏矩阵 

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵，但是对于这个“远远多于”并没有准确的定量规定。

比如

稀疏矩阵的例子

行优先与列优先   映射

对于一个二维数组，外观上看是一个矩阵，但是电脑内存是线性存储的，所以电脑会自动按照一定的规则，去把二维数组转换为地址连续的块放到内存中，这些规则分为行优先和列优先

比如下面这个矩阵

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

如果按行优先，放到内存就是1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

列优先就是1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16

我们在矩阵的压缩存储中，通常的策略就是把二维矩阵通过一定的下标（i，j）的映射规则放入到一维数组中，比如说呢，下面这个对称矩阵

2	4
4	2

放到一维数组a中只需包含 2 4，分别为a[0]和a[1]，数组的下标0与1与矩阵Ai,j的元素下标i和j的关系就是所谓的映射，这也是定量计算的重点！

二.特殊矩阵存储策略 

1.对称矩阵

设有对称矩阵A[i][j]如下图：（aᵢ,ⱼ=aⱼ,ᵢ ）

 存储策略：只存储主对角线＋下三角区（或主对角线+上三角区），以主对角线+下三角区为例，按照行优先把这些元素放入到一维数组中，就得到了下面的样子的一维数组：

a₁₁

a₂₁

a₂₂

a₃₁

...

aₙ,ₙ₋₂

aₙ,ₙ₋₁

aₙ,ₙ

这个一维数组的大小是1+2+3+...+n=n*n(n+1)/2

下面来把行号和列号转换为数组下标： 

aᵢ,ⱼ是第i行的元素，所以前面还有i-1行，元素总数为1+2+...+i-1=i*(i-1)/2

j代表其属于第j列，所以最终确定按照行优先的存储aᵢ,ⱼ应该在一维数组的第i*(i-1)/2+j个位置，但是由于数组是从0开始存的，所以对应下标为i*(i-1)/2+j-1

上述讨论的均为在下三角区的情形，此时i>=j

现在根据性质aᵢ,ⱼ=aⱼ,ᵢ可以得到矩阵所有元素与一维数组下标k的对应关系如下：

 2.三角矩阵

给出下面的下三角矩阵A[i][j]

存储策略:按照行优先将下三角区域（橙色部分）放入一位数组中，并将常数c放到最后一个位置

得到下图的一位数组

a₁₁

a₂₁

a₂₂

a₃₁

...

aₙ,ₙ₋₁

aₙ,ₙ

c

这个一位数组的大小为：1+2+3+...+n+1=n*n(n+1)/2+1

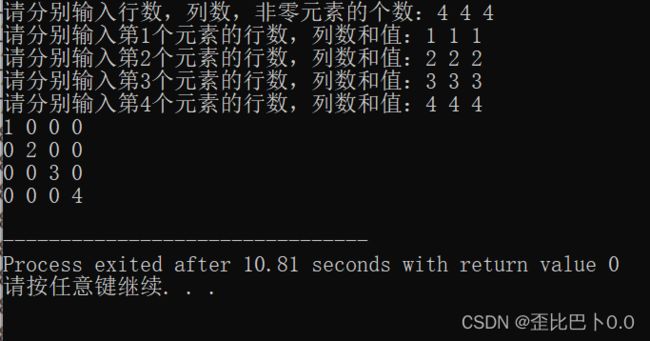
这个映射关系和对称矩阵几乎一样，唯一不同的是当i

 再来看上三角矩阵

给出下面的上三角矩阵A[i][j]

可以按照行优先原则，把上三角区域的元素（绿色区域），放入一位数组中，并在最后一个位置放入常数c，即可得到下面的一维数组

a₁₁

a₁₂

a₁₃

...

a₁,ₙ

...

aₙ,ₙ

c

这个的数组大小与下三角的一样，对于一个元素aᵢ,ⱼ，第i行的元素要存n-i+1个元素，第i-1行要存n-i+2个元素，所以前i-1行的元素总数为n+n-1+...+n-i+2，由于在第j列,所以对应第i行的第j-i+1个元素，总的来说，就是数组中的第n+n-1+...+n-i+2+j-i+1个元素，在数组中下标从0开始所以为n+n-1+...+n-i+2+j-i

综上，可以得到如下的映射关系

 3.带状矩阵

给出下面的带状矩阵A[i][j]

 存储策略，按照行优先的原则，只存储带状部分，便可以得到下面的一维数组：

a₁₁

a₁₂

a₂₁

a₂₂

...

aₙ₋₁,ₙ

aₙ,ₙ₋₁

aₙ,ₙ

先计算一维数组的大小，每行三个元素，共n行，3*n，但第一行和最后一行仅仅2个元素，所以总共个数为3*n-2

下面研究映射关系：

当|i-j|>1时，值就是0

当当|i-j|<=1时，对于一个元素aᵢ,ⱼ，前i-1行，每行有三个，第一行少了一个，总共为3*(i-1)-1个元素，而且找规律可以知道，这个元素在第i行是第j-i+2个元素，所以总共是数组的第3*(i-1)-1+j-i+2个元素即第2*i+j-2个元素，对应数组下标为2*i+j-3

所以映射关系为

下面再来探讨一个逆问题，就是如果给出数组下标k，想要得到这个元素在第几行第几列怎么办呢？

首先，这个元素是第k+1个元素，假设它在第i行第j列，那么前i-1行元素总数为3*（i-1）-1，前i行元素总数为3*i-1，满足下面的不等式

 3*（i-1）-1

解得：i>=(k+2)/3

为了让这个i“刚好大于(k+2)/3”,让其向上取整，即i=⌈(k+2)/3⌉（提示：⌈⌉是向上取整，⌊⌋是向下取整）

然后再根据我们上面得出的关系式：k=2*i+j-3综合可得j的值，从而得到i和j即为元素行数和列数

4.稀疏矩阵

给出下面这个稀疏矩阵

 给出两个方法去存储它

第一个方式是顺序存储，通过一个包含行号、列号、元素值的三元组，去进行存储，比如这个矩阵，我们可以用三元组表示为：

行数  i	列数  j	值  v
1	3	4
1	6	5
2	2	3
2	4	9
3	5	7
4	2	2

可以定义包括i j v 的结构体数组

第二个方法是链式存储的十字链表法

可以表示为下图：

 对于每一个非0元素的结点，包含3个数据域行数i、列数j、元素值v，和两个指针域，左边的指针指向同列的下一个元素，右边的指针指向同行的下一个元素

下面给出十字链表的c语言实现代码以及效果图，如果代码有不足之处，可以指出！：

#include
#include
#include
#define OVERFLOW -1
#define OK 1
typedef  int ElemType;
typedef  int Status;
typedef struct OLNode{
	int i,j;
	ElemType e;
	struct OLNode *right,*down;
}OLNode,*OLink;
typedef struct {
	OLink *rhead,*chead; //行和列链表头指针向量基地址由CreatSMatrix分配 
	int mu,nu,tu;//稀疏矩阵行数，列数和非0元素个数 
}CrossList,*CrossListPtr; 

Status CreatSMatrix_OL (CrossListPtr M)
{
	//创建稀疏矩阵M，采用十字链表存储表示
	if(M) free(M);//释放M原有的内存
	M=(CrossListPtr)malloc(sizeof(CrossList));
	int m,n,t,a;
	int i,j,e;
	int cnt; 
	OLNode *p,*q;
	printf("请分别输入行数，列数，非零元素的个数：");
	scanf("%d%d%d",&m,&n,&t);//输入M的行数列数和非零元素个数
    M->mu=m;M->nu=n;M->tu=t;//赋到M里面
	if(!(M->rhead=(OLink *)malloc((m+1)*sizeof(OLink)))) exit(OVERFLOW);
	if(!(M->chead=(OLink *)malloc((n+1)*sizeof(OLink)))) exit(OVERFLOW);
	//分别为行链表头和列链表头分配内存
	for(a=1;a<=m;a++) M->rhead[a]=NULL;
	for(a=1;a<=n;a++) M->chead[a]=NULL;
	//使各行列链表都为空表
	
	for(cnt=1;cnt<=t;cnt++)//按任意次序输入非0元素，
	{
		printf("请分别输入第%d个元素的行数，列数和值：",cnt);
		scanf("%d%d%d",&i,&j,&e);
		if(!(p=(OLNode *)malloc(sizeof(OLNode)))) exit(OVERFLOW);
		p->i=i;p->j=j;p->e=e;//生成结点
		if(M->rhead[i]==NULL||M->rhead[i]->j>j) 
		{
			p->right=M->rhead[i]; M->rhead[i]=p;
		} //如果行链表数组的第i行的头结点右边是空或者右边元素的列数比j大，让p左边被链表的rhead指针指住
		else
		{
			for(q=M->rhead[i];(q->right)&&q->right->jright);//找到将要插入的合适位置，要么是右边为空，要么q->right->jright=q->right;q->right=p;//插入 
		 } //行插入 
		 if(M->chead[j]==NULL||M->chead[j]->i>i) 
		 {
		 	p->down=M->chead[j];M->chead[j]=p;
		 }
		 else
		 {
		 	for(q=M->chead[j];(q->down)&&q->down->idown);
		 	p->down=q->down;q->down=p;
		 }//列插入 
	} 
	//下面检验是否存储成功 
    int check[10][10];
	memset(check,0,sizeof(check));
	int i1,j1;
	OLink p1;
	for(i1=1;i1<=M->mu;i1++)
	{
		for(p1=M->rhead[i1];p1;p1=p1->right)
		{
			check[i1][p1->j]=p1->e;
		}	
		
    } 
    for(i1=1;i1<=M->mu;i1++)
    {
    	for(j1=1;j1<=M->nu;j1++)
		{
			printf("%d ",check[i1][j1]);
		} 
		printf("\n");
	}
	return OK;
}
int main()
{
	CrossListPtr M=NULL;
	CreatSMatrix_OL(M);
	return 0;
}

这是效果图：

 今天的文章就到这里了（`･ω･´）