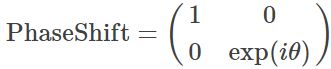基于QFT的量子加法器的原理与实现-mindspore quantum

1 量子Fourier变换

离散Fourier变换以一一个复向量$x_0,...,x_{N-1}$为输入，输出的数据是如下复向量$y_0,...,y_{N-1}$：
$$y_k\equiv \frac{1}{\sqrt{N}}\sum _{j=0}^{N-1}{x}_j{e}^{2\pi ijk/N}$$

量子Fourier变换是与它严格相同的变换。量子Fourier变换定义为，在一组标准正交基$|0⟩,...,|N-1⟩$上的一个线性算子，在基态上的作用为
$$|j⟩\to \frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{e}^{2\pi ijk/N}|k⟩$$

我们将状态$j$写成二进制形式$j=j_1{j}_2...j_n$，用记号$0.j_l{j}_{l+1}...j_m$表示二进制分数。

容易推导出量子Fourier变换的积形式：
$$\begin{array}{l}|j_1,...,j_n⟩\to \\ \frac{1}{2^{n/2}}\left[\left(|0⟩+e^{2\pi i0.j_n}|1⟩\right)\left(|0⟩+e^{2\pi i0.j_{n-1}{j}_n}|1⟩\right)...\left(|0⟩+e^{2\pi i0.j_1...j_{n-1}{j}_n}|1⟩\right)\right]\end{array}$$

量子Fourier变换的有效线路实现如下：
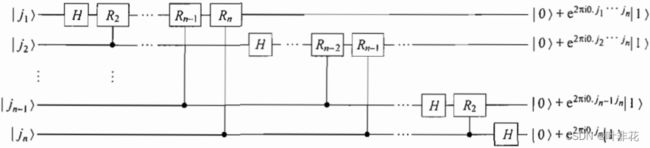其中门$R_k$表示酉变换

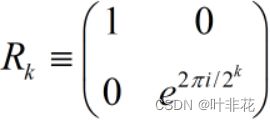
使用交换运算逆转量子比特的顺序，量子比特的状态为
$$\frac{1}{2^{n/2}}\left(|0⟩+e^{2\pi i0.j_n}|1⟩\right)\left(|0⟩+e^{2\pi i0.j_{n-1}{j}_n}|1⟩\right)...\left(|0⟩+e^{2\pi i0.j_1...j_{n-1}{j}_n}|1⟩\right)$$

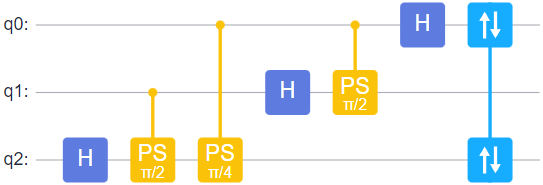
量子Fourier变换可使用如下语句实现

from mindquantum.algorithm.library import qft
circ = qft([2,1,0]) 
circ.svg()

图中的PS门为相位旋转门PhaseShift。

需要注意的是，q0 q1 q2寄存器对应的量子态为$|q_2{q}_1{q}_0⟩$。

2 量子加法器

若有$a=a_1{a}_2...a_n$和$b=b_1{b}_2...b_n$，欲计算$c=a+b$，根据量子Fourier变换的知识，我们可先制备出如下量子态$|cf⟩$
$$\frac{1}{2^{n/2}}\left(|0⟩+e^{2\pi i0.c_n}|1⟩\right)\left(|0⟩+e^{2\pi i0.c_{n-1}{c}_n}|1⟩\right)...\left(|0⟩+e^{2\pi i0.c_1...c_{n-1}{c}_n}|1⟩\right)$$
再利用逆Fourier变换即可得到$|c_1{c}_2...c_n⟩$。

2.1 不考虑最高位进位

观察到



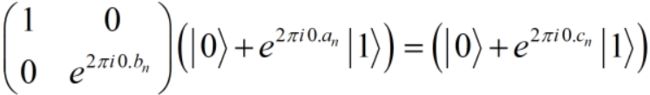
于是可使用如下线路制备$|cf⟩$，这里先不考虑最高位有进位的情况。

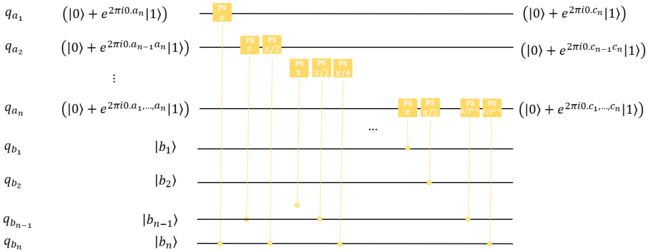
将这个线路记作MAdder（Modular Adder）。于是，量子加法器的线路如下（不考虑最高位进位）：

2.2 考虑最高位进位

考虑$a=a_1{a}_2...a_n$，$b=b_1{b}_2...b_n$，$c=a+b=c_1{c}_2...c_{n+1}$。$c_1=0$表示最高位无进位，$c_1=0$表示最高位有进位。

若考虑最高位进位，则需要给$a$增加一个量子比特存储进位项。
$$|a⟩=|0a_1,...,a_n⟩$$
对$|a⟩$做量子Fourier变换后

观察到

于是制备$|cf⟩$的线路如下

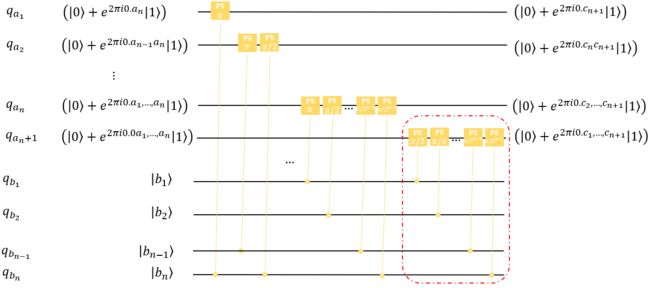
注意：红框里线路的旋转角相比于前面的线路均多除了一个2。
将上图线路记作Adder，完整的量子加法器线路如下

3 代码实现

导入一些用到的包

from mindquantum.algorithm.library import qft
from mindquantum.simulator import Simulator
from mindquantum.core.gates import  X, PhaseShift
from mindquantum.core.circuit import Circuit,dagger
import numpy as np

定义受控相位旋转操作

def _rn(k):
    return PhaseShift(2 * np.pi / 2 ** k)

def C_R(tq, cq, k):
    circ = Circuit()
    circ += _rn(k).on(tq, cq)
    return circ

定义adder，这里考虑了进位项

def m_adder(qa, qb):
    circ = Circuit()
    qa_num = len(qa)
    qb_num = len(qb)

    for q in range(qb_num):
        for i in range(qb_num - q - 1, qb_num):
            circ += C_R(qa[qa_num - q - 1], qb[qb_num - i - 1], i - (qb_num - q - 1) + 1)
        if qa_num > qb_num and q == (qb_num - 1):  # 进位的控制
            for i in range(qb_num - q - 1, qb_num):
                circ += C_R(qa[qa_num - q - 1 - 1], qb[qb_num - i - 1], i - (qb_num - q - 1) + 1 + 1)
    return circ

输入a和b的值（假设a,b都是3bit二进制数），并执行加法器

#定义存储a和b的寄存器qa,qb
qa = [3, 4, 5, 6]
qb = [0, 1, 2]

circ = Circuit()

# qa 输入a的值 001
# circ += X.on(5)
# circ += X.on(4)
circ += X.on(3)

# qb 输入b的值 111
circ += X.on(2)
circ += X.on(1)
circ += X.on(0)

#对qa执行量子Fourier操作
circ += qft([6, 5, 4, 3])

#执行加法操作
adder = m_adder(qa, qb)
circ += adder

#使用量子逆Four变换恢复出结果
circ += dagger(qft([6, 5, 4, 3]))

sim = Simulator('projectq', 7)
sim.apply_circuit(circ)
print(sim.get_qs(True))

circ.svg() #查看整个线路

1¦1000111⟩
结果保存在qa寄存器中即c=1000
qb寄存器中值不变，即b=111

参考资料

[1] Engin Şahin. Quantum arithmetic operations based on quantum fourier transform on signed integers. International Journal of Quantum Information. (2020) 2050035 (21 pages).