8.2 电压比较器(1)
电压比较器是对输入信号进行鉴幅与比较的电路,是组成非正弦波发生电路的基本单元电路,在测量和控制中有着相当广泛的应用。
一、概述
1、电压比较器的电压传输特性
电压比较器的输出电压 u O u_{\scriptscriptstyle O} uO 与输入电压 u I u_{\scriptscriptstyle I} uI 的函数关系 u O = f ( u I ) u_{\scriptscriptstyle O}=f(u_{\scriptscriptstyle I}) uO=f(uI) 一般用曲线来描述,称为电压传输特性。输入电压 u I u_{\scriptscriptstyle I} uI 是模拟信号,而输出电压 u O u_{\scriptscriptstyle O} uO 只有两种可能的状态,不是高电平 U O H U_{\scriptscriptstyle OH} UOH,就是低电平 U O L U_{\scriptscriptstyle OL} UOL,用以表示比较的结果。使 u O u_{\scriptscriptstyle O} uO 从 U O H U_{\scriptscriptstyle OH} UOH 跃变为 U O L U_{\scriptscriptstyle OL} UOL,或者从 U O L U_{\scriptscriptstyle OL} UOL 跃变为 U O H U_{\scriptscriptstyle OH} UOH 的输入电压称为阈值电压,或转折电压,记作 U T U_{\scriptscriptstyle T} UT。
为了正确画出电压传输特性,必须求出以下三个要素:
(1)输出电压高电平 U O H U_{\scriptscriptstyle OH} UOH 和输出低电平 U O L U_{\scriptscriptstyle OL} UOL;
(2)阈值电压 U T U_{\scriptscriptstyle T} UT;
(3)当 u I u_{\scriptscriptstyle I} uI 变化且经过 U T U_{\scriptscriptstyle T} UT 时, u O u_{\scriptscriptstyle O} uO 跃变的方向,即是从 U O H U_{\scriptscriptstyle OH} UOH 跃变为 U O L U_{\scriptscriptstyle OL} UOL,还是从 U O L U_{\scriptscriptstyle OL} UOL 跃变为 U O H U_{\scriptscriptstyle OH} UOH。
2、集成运放的非线性工作区
在电压比较器电路中,绝大多数集成运放不是处于开环状态(即没有引入反馈),就是只引入了正反馈,如图8.2.1(a)、(b)所示;图(b)中反馈通路为电阻网络。对于理想运放,由于差模增益无穷大,只要同相输入端与反向输入端之间有无穷小的差值电压,输出电压就将达到正的最大值或负的最大值,即输出电压 u O u_{\scriptscriptstyle O} uO 与输入电压 ( u P − u N ) (u_{\scriptscriptstyle P}-u_{\scriptscriptstyle N}) (uP−uN) 不再是线性关系,称集成运放工作在非线性工作区,其电压传输特性如图(c)所示。若集成运放的输出电压 u O u_{\scriptscriptstyle O} uO 的幅值为 ± U O M ±\,U_{\scriptscriptstyle OM} ±UOM,则当 u P > u N u_{\scriptscriptstyle P}>u_{\scriptscriptstyle N} uP>uN 时 u O = + U O M u_{\scriptscriptstyle O}=+\,U_{\scriptscriptstyle OM} uO=+UOM,当 u N > u P u_{\scriptscriptstyle N}>u_{\scriptscriptstyle P} uN>uP 时 u O = − U O M u_{\scriptscriptstyle O}=-\,U_{\scriptscriptstyle OM} uO=−UOM。并且由于理想运放的差模输入电阻无穷大,故净输入电流为零,即 i P = i N = 0 i_{\scriptscriptstyle P}=i_{\scriptscriptstyle N}=0 iP=iN=0。
3、电压比较器的种类
(1)单限比较器
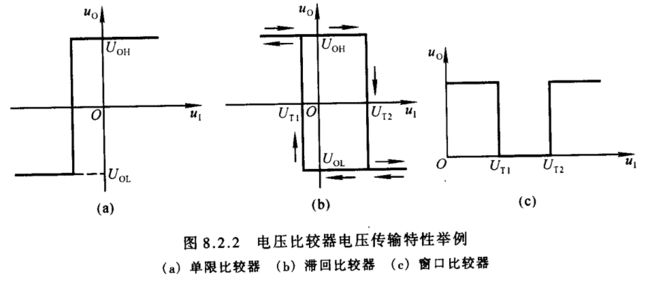
电路只有一个阈值电压,输入电压 u I u_{\scriptscriptstyle I} uI 逐渐增大或减小过程中,当通过 U T U_{\scriptscriptstyle T} UT 时,输出电压 u O u_{\scriptscriptstyle O} uO 产生跃变,从高电平 U O H U_{\scriptscriptstyle OH} UOH 跃变为低电平 U O L U_{\scriptscriptstyle OL} UOL,或者从 U O L U_{\scriptscriptstyle OL} UOL 跃变为 U O H U_{\scriptscriptstyle OH} UOH。图8.2.2(a)是某单限比较器的电压传输特性。
(2)滞回比较器
电路有两个阈值电压,输入电压 u I u_{\scriptscriptstyle I} uI 从小变大过程中使输出电压 u O u_{\scriptscriptstyle O} uO 产生跃变的阈值电压 U T 2 U_{\scriptscriptstyle T2} UT2,不等于从大变小过程中使输出电压 u O u_{\scriptscriptstyle O} uO 产生跃变的阈值电压 U T 1 U_{\scriptscriptstyle T1} UT1,电路具有滞回特性。它与单限比较器的相同之处在于:当输入电压向单一方向变化时,输出电压只跃变一次。图8.2.2(b)是某滞回比较器的电压传输特性。
(3)窗口比较器
电路有两个阈值电压,输入电压 u I u_{\scriptscriptstyle I} uI 从小变大或从大变小过程中使输出电压 u O u_{\scriptscriptstyle O} uO 产生两次跃变。例如,某窗口比较器的两个阈值电压 U T 1 U_{\scriptscriptstyle T1} UT1 小于 U T 2 U_{\scriptscriptstyle T2} UT2,且均大于零;输入电压 u I u_{\scriptscriptstyle I} uI 从零开始增大,当经过 U T 1 U_{\scriptscriptstyle T1} UT1 时, u O u_{\scriptscriptstyle O} uO 从高电平 U O H U_{\scriptscriptstyle OH} UOH 跃变为低电平 U O L U_{\scriptscriptstyle OL} UOL; u I u_{\scriptscriptstyle I} uI 继续增大,当经过 U T 2 U_{\scriptscriptstyle T2} UT2 时, u O u_{\scriptscriptstyle O} uO 又从 U O L U_{\scriptscriptstyle OL} UOL 跃变为 U O H U_{\scriptscriptstyle OH} UOH;电压传输特性如图8.2.2(c)所示,中间如开了个窗口,故此得名。窗口比较器与前两种比较器的区别在于:输入电压向单一方向变化过程中,输出电压跃变两次。
上述为常见的三种电压比较器,在实际应用中还有其它种类,如三态电压比较器。
二、单限比较器
1、过零比较器
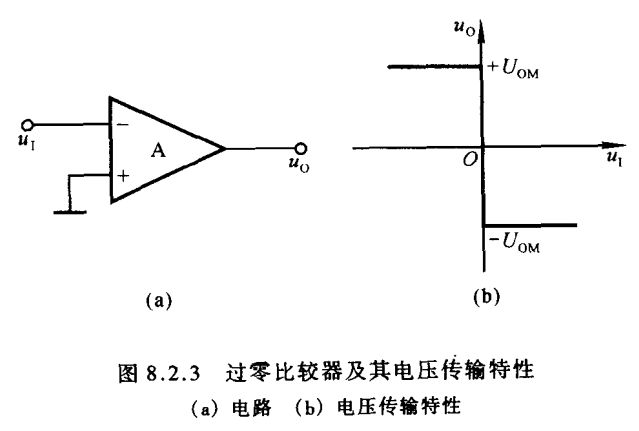
过零比较器,顾名思义,其阈值电压 U T = 0 V U_{\scriptscriptstyle T}=0\,\textrm V UT=0V。电路如图8.2.3(a)所示,集成运放工作在开环状态,其输出电压为 + U O M +U_{\scriptscriptstyle OM} +UOM 或 − U O M -U_{\scriptscriptstyle OM} −UOM。当输入电压 u I < 0 V u_{\scriptscriptstyle I}<0\,\textrm V uI<0V 时, U O = + U O M U_{\scriptscriptstyle O}=+U_{\scriptscriptstyle OM} UO=+UOM;当 u I > 0 V u_{\scriptscriptstyle I}>0\,\textrm V uI>0V 时, U O = − U O M U_{\scriptscriptstyle O}=-U_{\scriptscriptstyle OM} UO=−UOM。因此,电压传输特性如图(b)所示。若想获得 u O u_{\scriptscriptstyle O} uO 跃变方向相反的电压传输特性,则应在图(a)所示电路中将反向输入端接地,而在同相输入端接输入电压。
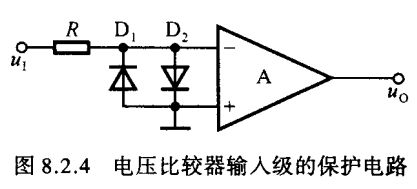
为了限制集成运放的差模输入电压,保护其输入级,可加二极管限幅电路,如图8.2.4所示。
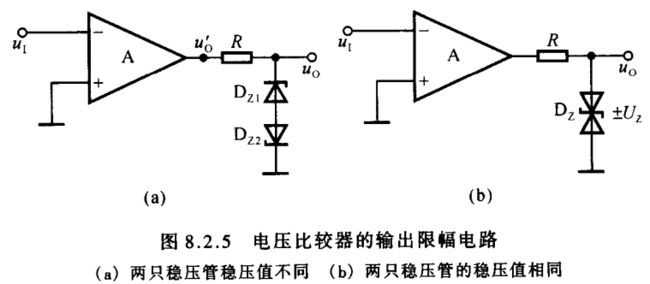
在实用电路中为了满足负载的需要,常在集成运放的输出端加稳压管限幅电路,从而获得合适的 U O L U_{\scriptscriptstyle OL} UOL 和 U O H U_{\scriptscriptstyle OH} UOH,如图8.2.5(a)所示。图中 R R R 为限流电阻,两只稳压管的稳定电压均应小于集成运放的最大输出电压 U O M U_{\scriptscriptstyle OM} UOM。设稳压管 D Z 1 D_{\scriptscriptstyle Z1} DZ1 的稳定电压为 U Z 1 U_{\scriptscriptstyle Z1} UZ1, D Z 2 D_{\scriptscriptstyle Z2} DZ2 的稳定电压为 U Z 2 U_{\scriptscriptstyle Z2} UZ2; D Z 1 D_{\scriptscriptstyle Z1} DZ1 和 D Z 2 D_{\scriptscriptstyle Z2} DZ2 的正向导通电压均为 U D U_{\scriptscriptstyle D} UD。当 u I < 0 V u_{\scriptscriptstyle I}<0\,\textrm V uI<0V 时,由于集成运放的输出电压 u O ′ = + U O M u_{\scriptscriptstyle O}'=+U_{\scriptscriptstyle OM} uO′=+UOM,使 D Z 1 D_{\scriptscriptstyle Z1} DZ1 工作在稳压状态, D Z 2 D_{\scriptscriptstyle Z2} DZ2 工作在正向导通状态,所以输出电压 u O = U O H = + ( U Z 1 + U D ) u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OH}=+(U_{\scriptscriptstyle Z1}+U_{\scriptscriptstyle D}) uO=UOH=+(UZ1+UD)。当 u I > 0 V u_{\scriptscriptstyle I}>0\,\textrm V uI>0V 时,由于集成运放的输出电压 u O ′ = − U O M u_{\scriptscriptstyle O}'=-U_{\scriptscriptstyle OM} uO′=−UOM,使 D Z 2 D_{\scriptscriptstyle Z2} DZ2 工作在稳压状态, D Z 1 D_{\scriptscriptstyle Z1} DZ1 工作在正向导通状态,所以输出电压 u O = U O L = − ( U Z 2 + U D ) u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OL}=-(U_{\scriptscriptstyle Z2}+U_{\scriptscriptstyle D}) uO=UOL=−(UZ2+UD)。若要求 U Z 1 = U Z 2 U_{\scriptscriptstyle Z1}=U_{\scriptscriptstyle Z2} UZ1=UZ2,则可以采用两只特性相同而又制作在一起的稳压管,其符号如图8.2.5(b)所示,导通时的端电压标为 ± U Z ±U_{\scriptscriptstyle Z} ±UZ。当 u I < 0 V u_{\scriptscriptstyle I}<0\,\textrm V uI<0V 时, u O = U O H = + U Z u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OH}=+U_{\scriptscriptstyle Z} uO=UOH=+UZ;当 u I > 0 V u_{\scriptscriptstyle I}>0\,\textrm V uI>0V 时, u O = U O L = − U Z u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OL}=-U_{\scriptscriptstyle Z} uO=UOL=−UZ。
限幅电路的稳压管还可跨接在集成运放的输出端和反向输入端之间,如图8.2.6所示。假设稳压管截止,则集成运放必然工作在开环状态,输出电压不是 + U O M +U_{\scriptscriptstyle OM} +UOM,就是 − U O M -U_{\scriptscriptstyle OM} −UOM;这样,必然导致稳压管击穿而工作在稳压状态, D Z D_{\scriptscriptstyle Z} DZ 构成负反馈通路,使反向输入端为 “虚地”,限流电阻上的电流 i R i_{\scriptscriptstyle R} iR 等于稳压管的电流 i Z i_{\scriptscriptstyle Z} iZ,输出电压 u O = ± U Z u_{\scriptscriptstyle O}=±U_{\scriptscriptstyle Z} uO=±UZ。可见,虽然图示电路中引入了负反馈,但它仍具有电压比较器的基本特征。
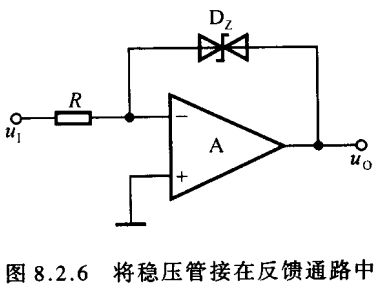
图8.2.6电路具有如下两个优点:一是由于集成运放的净输入电压和净输入电流均近似为零,从而保护了输入级;二是由于集成运放并没有工作到非线性区,因而在输入电压过零时,其内部的晶体管不需要从截止区逐渐进入饱和区,或从饱和区逐渐进入截止区,所以提高了输出电压的变化速度。
2、一般单限比较器
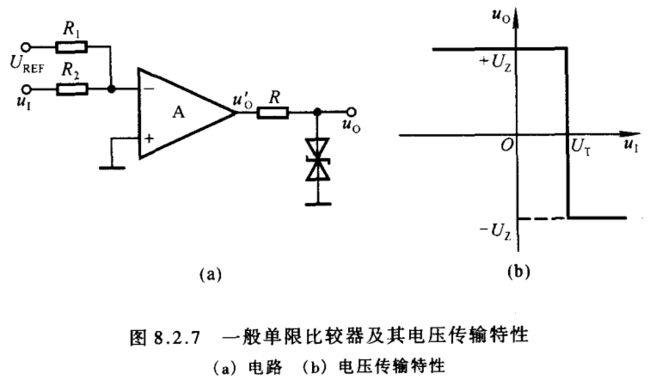
图8.2.7(a)所示为一般单限比较器, U R E F U_{\scriptscriptstyle REF} UREF 为外加参考电压。根据叠加原理,集成运放反相输入端的电位 u N = R 1 R 1 + R 2 u I + R 2 R 1 + R 2 U R E F u_{\scriptscriptstyle N}=\frac{R_1}{R_1+R_2}u_{\scriptscriptstyle I}+\frac{R_2}{R_1+R_2}U_{\scriptscriptstyle REF} uN=R1+R2R1uI+R1+R2R2UREF令 u N = u P = 0 u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P}=0 uN=uP=0,则求出阈值电压 U T = − R 2 R 1 U R E F ( 8.2.1 ) U_{\scriptscriptstyle T}=-\frac{R_2}{R_1}U_{\scriptscriptstyle REF}\kern 40pt(8.2.1) UT=−R1R2UREF(8.2.1)当 u I < U T u_{\scriptscriptstyle I}
根据(8.2.1)可知,只要改变参考电压的大小和极性,以及电阻 R 1 R_1 R1 和 R 2 R_2 R2 的阻值,就可以改变阈值电压的大小和极性。若要改变 u I u_{\scriptscriptstyle I} uI 过 U T U_{\scriptscriptstyle T} UT 时 u O u_{\scriptscriptstyle O} uO 的跃变方向,则应将集成运放的同相输入端和反相输入端所外接电路互换。
综上所述,分析电压传输特性三个要素的方法是:
(1)通过研究集成运放输出端所接的限幅电路来确定电压比较器的输出低电平 U O L U_{\scriptscriptstyle OL} UOL 和输出高电平 U O H U_{\scriptscriptstyle OH} UOH;
(2)写出集成运放同相输入端、反相输入端电位 u P u_{\scriptscriptstyle P} uP 和 u N u_{\scriptscriptstyle N} uN 的表达式,令 u P = u N u_{\scriptscriptstyle P}=u_{\scriptscriptstyle N} uP=uN,解得的输入电压就是阈值电压 U T U_{\scriptscriptstyle T} UT;
(3) u O u_{\scriptscriptstyle O} uO 在 u I u_{\scriptscriptstyle I} uI 过 U T U_{\scriptscriptstyle T} UT 时的跃变方向决定于 u I u_{\scriptscriptstyle I} uI 作用于集成运放的哪个输入端。当 u I u_{\scriptscriptstyle I} uI 从反相输入端(或通过电阻)输入时, u I < U T u_{\scriptscriptstyle I}
【例8.2.1】在图8.2.6所示电路中,稳压管的稳定电压 U Z = ± 6 V U_{\scriptscriptstyle Z}=±6\,\textrm V UZ=±6V;在图8.2.7(a)所示电路中, R 1 = R 2 = 5 kΩ R_1=R_2=5\,\textrm{kΩ} R1=R2=5kΩ,基准电压 U R E F = 2 V U_{\scriptscriptstyle REF}=2\,\textrm V UREF=2V,稳压管的稳定电压 U Z = ± 5 V U_{\scriptscriptstyle Z}=±5\,\textrm V UZ=±5V;它们的输入电压均为图8.2.8(a)所示的三角波。试分别画出两电路输出电压的波形。
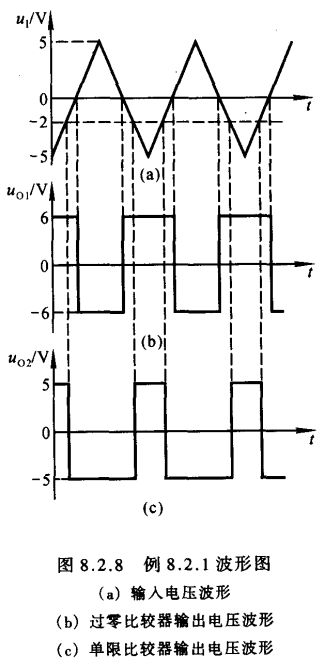
解: 根据图8.2.6所示电路可知,当 u I < 0 V u_{\scriptscriptstyle I}<0\,\textrm V uI<0V 时, u O 1 = + U Z = + 6 V u_{\scriptscriptstyle O1}=+U_{\scriptscriptstyle Z}=+6\,\textrm V uO1=+UZ=+6V;当 u I > 0 V u_{\scriptscriptstyle I}>0\,\textrm V uI>0V, u O 1 = − U Z = − 6 V u_{\scriptscriptstyle O1}=-U_{\scriptscriptstyle Z}=-6\,\textrm V uO1=−UZ=−6V;所以画出其输出电压 u O 1 u_{\scriptscriptstyle O1} uO1 的波形如图8.2.8(b)所示。
根据式(8.2.1) U T = − R 2 R 1 U R E F = − 2 V U_{\scriptscriptstyle T}=-\frac{R_2}{R_1}U_{\scriptscriptstyle REF}=-2\,\textrm V UT=−R1R2UREF=−2V因此,当 u I < − 2 V u_{\scriptscriptstyle I}<-2\,\textrm V uI<−2V 时, u O 2 = + U Z = + 5 V u_{\scriptscriptstyle O2}=+U_{\scriptscriptstyle Z}=+5\,\textrm V uO2=+UZ=+5V;当 u I > − 2 V u_{\scriptscriptstyle I}>-2\,\textrm V uI>−2V 时, u O 2 = − U Z = − 5 V u_{\scriptscriptstyle O2}=-U_{\scriptscriptstyle Z}=-5\,\textrm V uO2=−UZ=−5V;所以画出其输出电压 u O 2 u_{\scriptscriptstyle O2} uO2 的波形如图8.2.8(c)所示。
三、滞回比较器
在单限比较器中,输入电压在阈值电压附近的任何微小变化,都将引起输出电压的跃变,不管这种微小变化是来源于输入信号还是外部干扰。因此,虽然单限比较器很灵敏,但是抗干扰能力差。滞回比较器具有滞回特性,即具有惯性,因而也就具有一定的抗干扰能力。从反相输入端输入的滞回比较器电路如图8.2.9(a)所示,滞回比较器电路中引入了正反馈。

从集成运放输出端的限幅电路可以看出, u O = ± U Z u_{\scriptscriptstyle O}=±U_{\scriptscriptstyle Z} uO=±UZ。集成运放反相输入端电位 u N = u I u_{\scriptscriptstyle N}=u_{\scriptscriptstyle I} uN=uI,同相输入端电位 u P = R 1 R 1 + R 2 ⋅ U Z u_{\scriptscriptstyle P}=\frac{R_1}{R_1+R_2}\cdot U_{\scriptscriptstyle Z} uP=R1+R2R1⋅UZ令 u N = u P u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P} uN=uP,求出的 u I u_{\scriptscriptstyle I} uI 就是阈值电压,因此得出 ± U T = ± R 1 R 1 + R 2 ⋅ U Z ( 8.2.2 ) ±U_{\scriptscriptstyle T}=±\frac{R_1}{R_1+R_2}\cdot U_{\scriptscriptstyle Z}\kern 30pt(8.2.2) ±UT=±R1+R2R1⋅UZ(8.2.2)输出电压在输入电压 u I u_{\scriptscriptstyle I} uI 等于阈值电压时变化情况分析:假设 u I < − U T u_{\scriptscriptstyle I}<-U_{\scriptscriptstyle T} uI<−UT,那么 u N u_{\scriptscriptstyle N} uN 一定小于 u P u_{\scriptscriptstyle P} uP,因而 u O = + U Z u_{\scriptscriptstyle O}=+U_{\scriptscriptstyle Z} uO=+UZ,所以 u P = + U T u_{\scriptscriptstyle P}=+U_{\scriptscriptstyle T} uP=+UT。只有当输入电压 u I u_{\scriptscriptstyle I} uI 增大到 + U T +U_{\scriptscriptstyle T} +UT,再增大一个无穷小量时,输出电压 u O u_{\scriptscriptstyle O} uO 才会从 + U Z +U_{\scriptscriptstyle Z} +UZ 跃变为 − U Z -U_{\scriptscriptstyle Z} −UZ。同理,假设 u I > + U T u_{\scriptscriptstyle I}>+U_{\scriptscriptstyle T} uI>+UT,那么 u N u_{\scriptscriptstyle N} uN 一定大于 u P u_{\scriptscriptstyle P} uP,因而 u O = − U Z u_{\scriptscriptstyle O}=-U_{\scriptscriptstyle Z} uO=−UZ,所以 u P = − U T u_{\scriptscriptstyle P}=-U_{\scriptscriptstyle T} uP=−UT。只有当输入电压 u I u_{\scriptscriptstyle I} uI 减小到 − U T -U_{\scriptscriptstyle T} −UT,再减小一个无穷小量时,输出电压 u O u_{\scriptscriptstyle O} uO 才会从 − U Z -U_{\scriptscriptstyle Z} −UZ 跃变为 + U Z +U_{\scriptscriptstyle Z} +UZ。可见, u O u_{\scriptscriptstyle O} uO 从 + U Z +U_{\scriptscriptstyle Z} +UZ 跃变为 − U Z -U_{\scriptscriptstyle Z} −UZ 和 u O u_{\scriptscriptstyle O} uO 从 − U Z -U_{\scriptscriptstyle Z} −UZ 跃变为 + U Z +U_{\scriptscriptstyle Z} +UZ 的阈值电压是不同的,电压传输特性如图8.2.9(b)所示。
从电压传输特性曲线上可以看出,当 − U T < u I < + U T -U_{\scriptscriptstyle T}
实际上,由于集成运放的开环差模增益不是无穷大,只有当它的差模输入电压足够大时,输出电压 u O u_{\scriptscriptstyle O} uO 才为 ± U Z ±U_{\scriptscriptstyle Z} ±UZ。 u O u_{\scriptscriptstyle O} uO 在从 + U Z +U_{\scriptscriptstyle Z} +UZ 变为 − U Z -U_{\scriptscriptstyle Z} −UZ 或从 − U Z -U_{\scriptscriptstyle Z} −UZ 变为 + U Z +U_{\scriptscriptstyle Z} +UZ 的过程中,随着 u I u_{\scriptscriptstyle I} uI 的变化,将经过线性区,并需要一定的时间。滞回比较器中引入了正反馈,加快了 u O u_{\scriptscriptstyle O} uO 的转换速度。例如,当 u O = + U Z u_{\scriptscriptstyle O}=+U_{\scriptscriptstyle Z} uO=+UZ、 u P = + U T u_{\scriptscriptstyle P}=+U_{\scriptscriptstyle T} uP=+UT 时,只要 u I u_{\scriptscriptstyle I} uI 略大于 + U T +U_{\scriptscriptstyle T} +UT 足以引起 u O u_{\scriptscriptstyle O} uO 的下降,就会产生如下的正反馈过程:
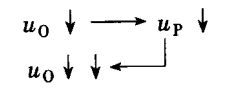
即 u O u_{\scriptscriptstyle O} uO 的下降导致 u P u_{\scriptscriptstyle P} uP 下降,而 u P u_{\scriptscriptstyle P} uP 的下降又使得 u O u_{\scriptscriptstyle O} uO 进一步下降,反馈的结果使 u O u_{\scriptscriptstyle O} uO 迅速变为 − U Z -U_{\scriptscriptstyle Z} −UZ,从而获得较为理想的电压传输特性。
为使滞回比较器的电压传输特性曲线向左或向右平移,需将两个阈值电压叠加相同的正电压或负电压。把电阻 R 1 R_1 R1 的接地端接参考电压 U R E F U_{\scriptscriptstyle REF} UREF,可达到此目的,如图8.2.10(a)所示,图中同相输入端的电位 u P = R 2 R 1 + R 2 U R E F ± R 1 R 1 + R 2 U Z u_{\scriptscriptstyle P}=\frac{R_2}{R_1+R_2}U_{\scriptscriptstyle REF}±\frac{R_1}{R_1+R_2}U_{\scriptscriptstyle Z} uP=R1+R2R2UREF±R1+R2R1UZ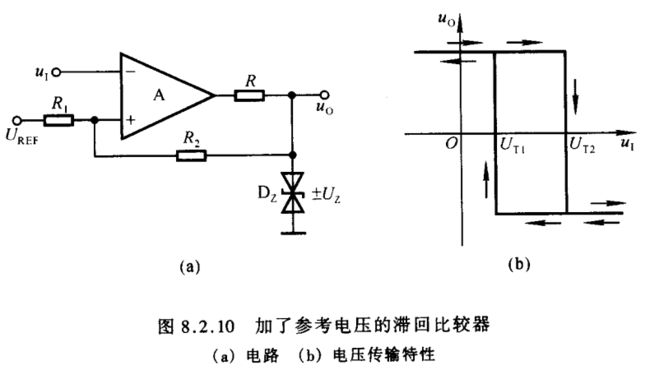
令 u N = u P u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P} uN=uP,求出的 u I u_{\scriptscriptstyle I} uI 就是阈值电压,因此得出 { U T 1 = R 2 R 1 + R 2 U R E F − R 1 R 1 + R 2 U Z ( 8.2.3 a ) U T 2 = R 2 R 1 + R 2 U R E F + R 1 R 1 + R 2 U Z ( 8.2.3 b ) \left\{\begin{matrix}U_{\scriptscriptstyle T1}=\displaystyle\frac{R_2}{R_1+R_2}U_{\scriptscriptstyle REF}-\frac{R_1}{R_1+R_2}U_{\scriptscriptstyle Z}\kern 20pt(8.2.3a)\\U_{\scriptscriptstyle T2}=\displaystyle\frac{R_2}{R_1+R_2}U_{\scriptscriptstyle REF}+\frac{R_1}{R_1+R_2}U_{\scriptscriptstyle Z}\kern 20pt(8.2.3b)\end{matrix}\right. ⎩ ⎨ ⎧UT1=R1+R2R2UREF−R1+R2R1UZ(8.2.3a)UT2=R1+R2R2UREF+R1+R2R1UZ(8.2.3b)两式中第一项是曲线在横轴左移或右移的距离,当 U R E F > 0 V U_{\scriptscriptstyle REF}>0\,\textrm V UREF>0V 时,图(a)所示电路的电压传输特性如图(b)所示,改变 U R E F U_{\scriptscriptstyle REF} UREF 的极性即可改变曲线平移的方向。
【例8.2.2】现测得某电路输入电压 u I u_{\scriptscriptstyle I} uI 和输出电压 u O u_{\scriptscriptstyle O} uO 的波形如图8.2.11(a)、(b)所示。
(1)判断该电路是哪种电压比较器,并求解电压传输特性;
(2)若要使 U T 1 = 2 V U_{\scriptscriptstyle T1}=2\,\textrm V UT1=2V, U T 2 = − 4 V U_{\scriptscriptstyle T2}=-4\,\textrm V UT2=−4V,则应在电路中采取什么措施?
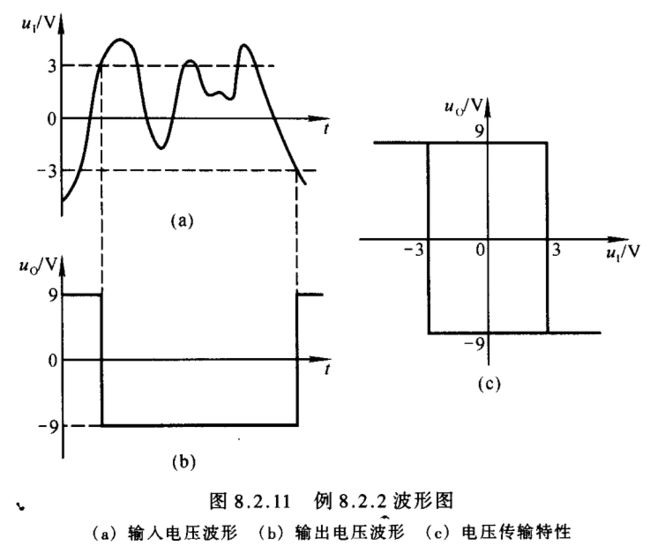
解: (1)从图8.2.11(b)所示 u O u_{\scriptscriptstyle O} uO 的波形可知,输出高、低电平分别为 ± U Z = ± 9 V ±U_{\scriptscriptstyle Z}=±9\,\textrm V ±UZ=±9V;从 u O u_{\scriptscriptstyle O} uO 与 u I u_{\scriptscriptstyle I} uI 的波形关系可知,阈值电压 ± U T = ± 3 V ±U_{\scriptscriptstyle T}=±3\,\textrm V ±UT=±3V;因为当 u I < − 3 V u_{\scriptscriptstyle I}<-3\,\textrm V uI<−3V 时 u O = U O H u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OH} uO=UOH,当 u I > + 3 V u_{\scriptscriptstyle I}>+3\,\textrm V uI>+3V 时 u O = U O L u_{\scriptscriptstyle O}=U_{\scriptscriptstyle OL} uO=UOL,说明输入信号从反相输入端输入;因为当 − 3 V < u I < + 3 V -3\,\textrm V
(2)将 U T 1 = 2 V U_{\scriptscriptstyle T1}=2\,\textrm V UT1=2V、 U T 2 = − 4 V U_{\scriptscriptstyle T2}=-4\,\textrm V UT2=−4V 与原阈值电压 U T 1 = 3 V U_{\scriptscriptstyle T1}=3\,\textrm V UT1=3V、 U T 2 = − 3 V U_{\scriptscriptstyle T2}=-3\,\textrm V UT2=−3V 相比可知,它们均在原数值上减 1 V 1\,\textrm V 1V,说明电压传输特性向左平移 1 V 1\,\textrm V 1V,故该电路如图8.2.10(a)所示,且 U R E F < 0 U_{\scriptscriptstyle REF}<0 UREF<0。
U R E F U_{\scriptscriptstyle REF} UREF 的数值应满足 R 2 R 1 + R 2 ⋅ U R E F = − 1 ( 8.2.4 ) \frac{R_2}{R_1+R_2}\cdot U_{\scriptscriptstyle REF}=-1\kern 30pt(8.2.4) R1+R2R2⋅UREF=−1(8.2.4)原电路阈值电压表达式为 ± U T = ± R 1 R 1 + R 2 ⋅ U Z ±U_{\scriptscriptstyle T}=±\displaystyle\frac{R_1}{R_1+R_2}\cdot U_{\scriptscriptstyle Z} ±UT=±R1+R2R1⋅UZ,将 ± U T = ± 3 V ±U_{\scriptscriptstyle T}=±3\,\textrm V ±UT=±3V、 ± U Z = ± 9 V ±U_{\scriptscriptstyle Z}=±9\,\textrm V ±UZ=±9V,可得 R 1 : R 2 = 1 : 2 R_1:R_2=1:2 R1:R2=1:2,代入式(8.2.4)解得 U R E F = − 1.5 V U_{\scriptscriptstyle REF}=-1.5\,\textrm V UREF=−1.5V。
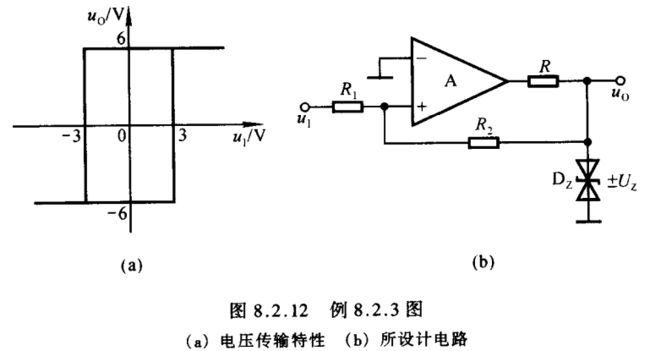
【例8.2.3】设计一个电压比较器,使其电压传输特性如图8.2.12(a)所示。除稳压管的限流电阻外,要求所用电阻阻值在 20 ∼ 100 k Ω 20\sim100\,\textrm kΩ 20∼100kΩ 之间。
解: 根据电压传输特性可知,输入电压作用于同相输入端,而且 u O = ± U Z = ± 6 V u_{\scriptscriptstyle O}=±U_{\scriptscriptstyle Z}=±6\,\textrm V uO=±UZ=±6V, U T 1 = − U T 2 = 3 V U_{\scriptscriptstyle T1}=-U_{\scriptscriptstyle T2}=3\,\textrm V UT1=−UT2=3V,电路没有外加基准电压,故电路如图8.2.12(b)所示。求解阈值电压的表达式: u P = R 2 R 1 + R 2 u I + R 1 R 1 + R 2 u O = u N = 0 u_{\scriptscriptstyle P}=\frac{R_2}{R_1+R_2}u_{\scriptscriptstyle I}+\frac{R_1}{R_1+R_2}u_{\scriptscriptstyle O}=u_{\scriptscriptstyle N}=0 uP=R1+R2R2uI+R1+R2R1uO=uN=0 ± U T = ± R 1 R 2 ⋅ U Z = ± 3 V ±U_{\scriptscriptstyle T}=±\frac{R_1}{R_2}\cdot U_{\scriptscriptstyle Z}=±3\,\textrm V ±UT=±R2R1⋅UZ=±3V解得 R 2 = 2 R 1 R_2=2R_1 R2=2R1。
若取 R 1 R_1 R1 为 25 k Ω 25\,\textrm kΩ 25kΩ,则 R 2 R_2 R2 应取 50 k Ω 50\,\textrm kΩ 50kΩ;若取 R 1 R_1 R1 为 50 k Ω 50\,\textrm kΩ 50kΩ,则 R 2 R_2 R2 应取为 100 k Ω 100\,\textrm kΩ 100kΩ。选取稳压管的稳定电压 ± U Z ±U_{\scriptscriptstyle Z} ±UZ 为 ± 6 V ±6\,\textrm V ±6V,限流电阻为 800 Ω 800\,\textrm Ω 800Ω。
四、窗口比较器
图8.2.13(a)所示为一种窗口比较器,外加参考电压 U R H > U R L U_{\scriptscriptstyle RH}>U_{\scriptscriptstyle RL} URH>URL,电阻 R 1 R_1 R1、 R 2 R_2 R2 和稳压管 D Z D_{\scriptscriptstyle Z} DZ 构成限幅电路。
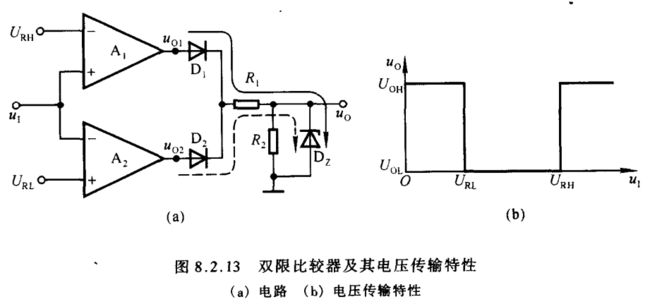
当输入电压 u I u_{\scriptscriptstyle I} uI 大于 U R H U_{\scriptscriptstyle RH} URH 时,必然大于 U R L U_{\scriptscriptstyle RL} URL,所以集成运放 A 1 A_1 A1 的输出 u O 1 = + U O M u_{\scriptscriptstyle O1}=+U_{\scriptscriptstyle OM} uO1=+UOM, A 2 A_2 A2 的输出 u O 2 = − U O M u_{\scriptscriptstyle O2}=-U_{\scriptscriptstyle OM} uO2=−UOM。使得二极管 D 1 D_1 D1 导通, D 2 D_2 D2 截止,电流通路如图中实线所标注,稳压管 D Z D_{\scriptscriptstyle Z} DZ 工作在稳压状态,输出电压 u O = + U Z u_{\scriptscriptstyle O}=+U_{\scriptscriptstyle Z} uO=+UZ。
当 u I u_{\scriptscriptstyle I} uI 小于 U R L U_{\scriptscriptstyle RL} URL 时,必然小于 U R H U_{\scriptscriptstyle RH} URH,所以 A 1 A_1 A1 的输出电压 u O 1 = − U O M u_{\scriptscriptstyle O1}=-U_{\scriptscriptstyle OM} uO1=−UOM, A 2 A_2 A2 的输出 u O 2 = + U O M u_{\scriptscriptstyle O2}=+U_{\scriptscriptstyle OM} uO2=+UOM。因此 D 2 D_2 D2 导通, D 1 D_1 D1 截止,电流通路如图中虚线所标注, D Z D_{\scriptscriptstyle Z} DZ 工作在稳压状态, u O u_{\scriptscriptstyle O} uO 仍为 + U Z +U_{\scriptscriptstyle Z} +UZ。
当 U R L < u I < U R H U_{\scriptscriptstyle RL}
U R H U_{\scriptscriptstyle RH} URH 和 U R L U_{\scriptscriptstyle RL} URL 分别为比较器的两个阈值电压,设 U R H U_{\scriptscriptstyle RH} URH 和 U R L U_{\scriptscriptstyle RL} URL 均大于零,则图8.2.13(a)所示电路的电压传输特性如图(b)所示。
通过以上三种电压比较器的分析,可得出如下结论:
(1)在电压比较器中,集成运放多工作在非线性区,输出电压只有高电平和低电平两种可能的情况。
(2)通常用电压传输特性来描述输出电压与输入电压的函数关系。
(3)电压传输特性的三个要素是输出电压的高、低电平,阈值电压和输出电压的跃变方向。输出电压的高、低电平决定于限幅电路;令 u P = u N u_{\scriptscriptstyle P}=u_{\scriptscriptstyle N} uP=uN 所求出的 u I u_{\scriptscriptstyle I} uI 就是阈值电压; u I u_{\scriptscriptstyle I} uI 等于阈值电压时输出电压的跃变方向决定于输入电压作用于同相输入端还是反相输入端。