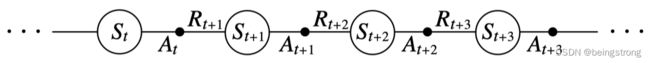《Reinforcement Learning: An Introduction》第6章笔记

Chapter 6 Temporal-Difference Learning

If one had to identify one idea as central and novel to reinforcement learning, it would undoubtedly be temporal-difference (TD) learning.

时序差分学习（temporal-difference (TD) learning）组合了Monte Carlo和DP的思想；它像Monte Carlo方法一样不需要环境动态模型，可以直接从经验中学习；它像DP方法一样是自举（bootstrap）方法。

6.1 TD Prediction

TD方法和Monte Carlo方法都使用经验来解决预测问题，给定策略$\pi$的一些经验，两种方法都使用这些经验中的非终止状态$S_t$来更新$v_{\pi }$的估计$V$。

一个适用于非平稳环境的简单的每次访问型Monte Carlo方法可用下式(6.1)表示，式中的$G_t$是从时刻t开始的实际回报，$\alpha$是固定步长参数（见第2章的式2.4），将这个方法称为常量$\alpha$ (constant-$\alpha$) MC方法。
$$V(S_t)\leftarrow V(S_t)+\alpha [G_t-V(S_t)](6.1)$$

相比于Monte Carlo方法必须等到一个序列回合的的结束来确定$V(S_t)$的增量（因为回合结束才能确定$G_t$）。TD方法只需要等待到下一个时刻。TD方法在时刻$t+1$ 立刻构造出目标，并且使用观察到的奖励$R_{t+1}$和估计$V(S_{t+1})$来做一次有用的更新，最简单的TD方法在状态转移到$S_{t+1}$并收到奖励$R_{t+1}$后立刻作如下更新：
$$V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)](6.2)$$
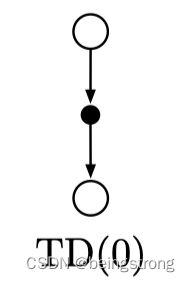
也就是说Monte Carlo方法更新的目标是$G_t$，而TD方法更新的目标是$R_{t+1}+\gamma V(S_{t+1})$，这个TD方法被称为$TD(0)$，或one-step TD， 因为它是本书第12章的$TD(\lambda )$和第7章的n-step TD的特例。下图是$TD(0)$的一个流程示意。

因为$TD(0)$根据已有估计来进行更新，我们说它是一个自举(bootstrapping)方法，就像DP方法一样。在第3章学过：
$$\begin{array}{rl}{v}_{\pi }(s)& \dot{=}{\mathbb{E}}_{\pi }[G_t\mid S_t=s](6.3)\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}\mid S_t=s](from(3.9))\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})\mid S_t=s](6.4)\end{array}$$

大致来说，Monte Carlo方法使用（6.3）式的估计值来作为目标，而DP方法使用（6.4）式的估计值来作为目标。

• Monte Carlo 方法的目标是一个估计值，是因为（6.3）式的期望值是未知的，用样本回报来代替实际的期望回报
• DP方法的目标是一个估计值，不是因为期望值的原因，因为它会假设由环境动态模型来提供期望值，真正的原因是因为真实的$v_{\pi }(S_{t+1})$是未知的，使用了当前估计$V(S_{t+1})$来代替。
• TD方法的目标是一个估计值是有两个原因：它采样得到（6.4）式中的期望值，并且使用当前的估计值$V$来代替真实值$v_{\pi }$。所以TD方法结合Monlo Carlo采样方法和DP自举法。

下图是$TD(0)$方法的回溯图，回溯图中的顶部状态节点的价值的估计值是根据它到一个直接后继状态节点的单次样本转移来更新的。将TD和Monte Carlo方法的更新称作采样更新（sample updates），采样更新和DP方法使用的期望更新不一样，它的计算基于采样得到的单个后继节点的样本数据，而不是所有可能后继节点的完整分布。

在式（6.2）的$TD(0)$更新中，括号里的数值是一种误差，被称为TD误差（TD error），如下式所示，它衡量是$S_t$的估计值与更好的估计值$R_{t+1}+\gamma V(S_{t+1})$之间的差异，在强化学习中会以各种形式出现。
$${\delta }_t\dot{=}{R}_{t+1}+\gamma V(S_{t+1})-V(S_t)(6.5)$$

每个时刻的TD误差是当前时刻估计的误差，但是因为它依赖于下一个状态和下一个收益，$V(S_t)$的误差要到时刻$t+1$才获得。

如果价值函数数组V在一个回合中没有改变（Monte Carlo方法就是），那么Monte Carlo 误差可以被写成TD误差之和：
$$\begin{array}{rl}{G}_t-V(S_t)& =R_{t+1}+\gamma G_{t+1}-V(S_t)+\gamma V(S_{t+1})-\gamma V(S_{t+1})(from(3.9))\\ & ={\delta }_t+\gamma (G_{t+1}-V(S_{t+1}))\\ & ={\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2(G_{t+2}-V(S_{t+2}))\\ & ={\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2}+\cdots +{\gamma }^{T-t-1}{\delta }_{T-1}+{\gamma }^{T-t}(G_T-V(S_T))\\ & ={\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2}+\cdots +{\gamma }^{T-t-1}{\delta }_{T-1}+{\gamma }^{T-t}(0-0)\\ & =\sum _{k=t}^{T-1}{\gamma }^{k-t}{\delta }_k(6.6)\end{array}$$

如果在一个回合中V变化了（如$TD(0)$中V不断被更新），那么这个等式就不准确，但是如果步长足够小，等式仍能近似成立。

6.2 Advantages of TD Prediction Methods

TD 方法有什么优势？

• 相比于DP方法，TD方法不需要一个动态环境模型。
• 相比于Monte Carlo方法，TD方法运用了在线的、完全递增的方法来实现。相比于Monte Carlo方法需要等待一个回合结束，TD方法只需要等待到下一个时刻。

TD方法能保证结果收敛到正确的值吗？答案是肯定的，对于任意固定型策略$\pi$，$TD(0)$已经被证明能够收敛到$v_{\pi }$。如果步长参数是一个足够小的常数，那么它的均值能收敛到$v_{\pi }$。如果步长参数根据第2章的随机近似条件（2.7）逐渐变小，则它能以概率1收敛。当然大多数收敛证明只适用于式（6.2）讨论的基于表格的算法，但有些也适用于适用广义线性函数近似的情况，将在第9章中讨论。

那TD和Monte Carlo方法哪个收敛更快？这个目前还是开放性的问题，没有人能够从数学上证明某种方法比另一种方法更快收敛。不过在实践中，TD方法在随机任务上通常比常量$\alpha$ MC方法更快收敛。

6.3 Optimality of TD(0)

批量更新（batch updating）：如果只有有限的经验，给定近似价值函数$V$，在访问非终止状态的每个时刻t，使用式（6.1）或式（6.2）计算相应的增量，但是价值函数仅根据所有增量的和改变一次。然后，利用新的值函数再次处理所有可用的经验，产生新的总增量，依次类推直到价值函数收敛。因为只有在处理了整批(batch)的训练数据后才进行更新，所以称这种方法为批量更新。

• 在批量更新下，只要选择足够小的步长参数$\alpha$，$TD(0)$就能确定地收敛到与$\alpha$无关的唯一结果。批量$TD(0)$总是找出完全符合马尔科夫过程模型的最大似然估计参数。

• 而常数$\alpha$ MC方法在相同条件下也能确定地收敛，但是会收敛到不同的结果。批量Monte Carlo方法总是找出最小化训练集上均方误差的估计。

最大似然估计与确定性等价估计：

• 最大似然估计（maximum-likelihood estimate）： 一个参数的最大似然估计是使生成训练数据的概率最大的参数值。
• 确定性等价估计（certainty-equivalence estimate）: 它假设潜在过程参数的估计是确定性的而不是近似的。比如在这一章的例子6.4中，马尔科夫过程模型参数的最大似然估计可以很直观地从观察到的多回合序列中得到：从i到j的转移概率估计值，就是观察数据中从i出发转移到j的次数占从i出发的所有转移次数的比例。而相应的期望奖励则是在这些转移中观察到的奖励的平均值。我们可以据此来估计价值函数，并且如果模型是正确的，则我们的估计也就完全正确。

批量$TD(0)$通常收敛到的就是确定性等价估计。这一点有助于解释为什么批量TD方法比批量Monte Carlo方法更快的收敛。 而对在线TD和Monte Carlo方法的效率的比较还没有定论。

虽然确定性等价估计在某种程度上是一个最优方案，但是直接计算它几乎是不可能的。如果$n=|\mathcal{S}|$是状态数，那么仅仅建立过程的最大似然估计就可能需要$n^2$的内存，如果按传统方法，计算相应的价值函数则需要$n^3$数量级的步骤。而TD方法则可以使用不超过n的内存，并通过在训练集上反复计算来逼近同样的答案，这一优势是相当惊人的；对于状态空间巨大的任务，TD方法可能是唯一可行的逼近确定性等价解的方法。

6.4 Sarsa: On-policy TD control

本节开始使用TD预测方法来解决控制问题，仍然遵循GPI的模式。像Monte Carlo方法一样，也分为on-policy和off-policy两种方法。

本节是on-policy TD控制算法Sarsa， 对于on-policy方法，我们必须对所有状态s和动作a，估计出在当前的行动策略下的$q_{\pi }(s,a)$。假设有一个如下图所示的，状态和动作交替出现的序列：

前面学过的状态价值的更新规则，也适用于状态-动作对：
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)](6.7)$$

每次从非终止状态的$S_t$进行一次转移之后，就进行如上式所示的一次更新，如果$S_{t+1}$是终止状态，则$Q(S_{t+1},A_{t+1})$为0。因为这个规则使用了描述这个事件的五元组$(S_t,A_t,R_{t+1},S_{t+1},A_{t+1})$的所有元素，所以这个算法被命名为Sarsa。Sarsa算法的回溯图如下图。

因为Sarsa是on-policy方法，所以我们持续地为行为策略$\pi$估计其动作价值函数$q_{\pi }$，同时以$q_{\pi }$为基础，朝着贪心的方向来改变策略$\pi$。Sarsa算法的一般形式如下图所示。

Sarsa算法的收敛性质取决于策略对于Q值的依赖，比如，可以使用$ϵ-greedy$或$ϵ-soft$策略。只要所有“状态-动作”对都被无限次访问到，并且贪心策略在极限情况下能够收敛（这个收敛过程可以通过令$ϵ=1/t$来实现），Sarsa就能以1的概率收敛到最优策略和动作。

6.5 Q-learning: Off-policy TD control

Q-learning是off-policy算法，于1989年提出，由下式定义：
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a)-Q(S_t,A_t)](6.8)$$
在这里，待学习的动作价值函数Q采用了对最优动作价值函数$q_{\ast }$的直接近似作为学习目标，而与用于生成agent决策序列轨迹的行为策略是什么无关。（而Sarsa的学习目标使用的是待学习的动作价值函数本身，由于它的计算需要知道下一时刻的动作$A_{t+1}$，所以与生成数据的行为策略是相关的）

Q-learning学习算法的流程如下图

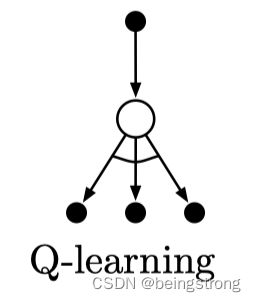
Q-learning学习算法的回溯图如下图：

6.6 Expected Sarsa

如果将Q-learning算法中的 下一个”状态-价值“对取最大值 替换成取期望的学习算法，即按照如下规则更新：
$$\begin{array}{rl}Q(S_t,A_t)& \leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma {\mathbb{E}}_{\pi }[Q(S_{t+1},A_{t+1})\mid S_{t+1}]-Q(S_t,A_t)]\\ & \leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \sum _a\pi (a|S_{t+1})Q(S_{t+1},a)-Q(S_t,A_t)](6.9)\end{array}$$
该遵循着Q-learning的模式，给定下一个状态$S_{t+1}$，这个算法确定地向期望意义上的Sarsa算法所决定的方向上移动，因此这个算法被称为期望Sarsa（Expected Sarsa），其回溯图如下：

期望Sarsa 相比于Sarsa计算更复杂，但是它消除了sarsa因为随机选择$A_{t+1}$而产生的方差。在相同数量的经验下，期望Sarsa的表现会更好。

期望Sarsa可以用作on-policy 算法，也可以采用与目标策略$\pi$不同的行为策略来生成行为，这时期望Sarsa就是off-policy 算法。除了少许增加计算量外，期望sarsa更优于Sarsa和Q-learning。

6.7 Maximization Bias and Double Learning

最大化偏差（maximization bias）：我们学到过的控制算法在构建目标时都包含了最大化的操作。比如，Q-learning的目标策略是根据所有动作价值的最大值来选取动作的贪心策略，Sarsa使用$ϵ-greedy$策略，也包含了最大化操作。在这些算法中，在估计值的基础上进行最大化可以被看作隐式地对其最大值进行估计，这会产生一个显著的正偏差。

最大化偏差例子：假设在状态s下可以选择多个动作a，这些动作在该状态下的真实价值$q(s,a)$全为0，但是它们的估计值$Q(s,a)$是不确定的，可能有些大于零，有些小于零。真实值的最大值是零，但是估计值的最大值是正数，因此就产生了正偏差。

有没有算法来避免最大化偏差呢？double learning是一种解决方法，它的基本思想是：假设我们将样本划分为两个集合，并用它们学习两个独立的对真实价值$q(a),a\in \mathcal{A}$的估计$Q_1(a)$和 $Q_2(a)$，我们使用其中一个估计，如$Q_1(a)$，来确定最大的动作$A_{\ast }=argma{x}_a{Q}_1(a)$，再利用另一个$Q_2(a)$来计算其价值的估计$Q_2(A^{\ast })=Q_2(argma{x}_a{Q}_1(a))$。由于$\mathbb{E}[Q_2(A^{\ast })]=q(A^{\ast })$，所以这个估计是无偏的。我们也可以交换两个估计$Q_1(a)$和 $Q_2(a)$的角色再执行一遍上面这个过程，那么就又可以得到另一个无偏的估计$Q_1(argma{x}_a{Q}_2(a))$。

double learning中我们学习了两个估计值，但是对每个样本集合只需要更新一个估计值，所以它需要两倍的内存，但是每步不需要额外的计算量。

double learning的思想可以推广到为完备MDP设计的算法中，Q-learning的double learning版被称为Doulbe Q-learning。Doulbe Q-learning将所有的时刻一分为二。假设用抛硬币的方式进行划分，当硬币正面朝上时，进行如下更新：
$$Q_1(S_t,A_t)\leftarrow Q_1(S_t,A_t)+\alpha [R_{t+1}+\gamma Q_2(S_{t+1},{\mathrm{argmax}}_a{Q}_1(S_{t+1},a))-Q_1(S_t,A_t)](6.10)$$
如果硬币反面朝上，那么就交换$Q_1$和$Q_2$的角色进行同样的更新，这样就能更新$Q_2$。两个近似价值函数的地位是完全相同的，两者的估计值都可以在行动策略中使用，下图展示了一个完整算法流程。

6.8 Games, Afterstates, and Other Special Cases

本节说明了一个afterstates状态的概念，意在解释虽然我们想为不同的任务找到一个统一的解决方案，但是总会有一些任务用特定的方法来解决更好。

6.9 Summary

本章关键概念：

• TD学习
• 时序差分误差（TD error）
• on-policy sarsa算法
• off-policy sarsa算法

---

参考资料

1. 《Reinforcement Learning: An Introduction》Sutton, Richard S. and Andrew G. Barto. 第2版， 书籍网站 ，文中图片全部来自书籍。
2. https://github.com/ShangtongZhang/reinforcement-learning-an-introduction
3. https://github.com/YunlianMoon/reinforcement-learning-an-introduction-2nd-edition/tree/master