【2021CCPC 威海】A、D、G、J

A. Goodbye, Ziyin!

题意：
给一个无根树，判断有多少个节点能做二叉树的根。

题解：
度小于等于2：可做根。
度大于3，不可存在二叉树。

#include 
using namespace std;
#define ll long long
const int maxn=2e6+3;
#define sc scanf
#define pr printf
map<int,int>num;
int main() {
	int n,a,b;sc("%d",&n);
	int cnt=0;
	int t=n-1;
	int f=1;
	while(t--){
		sc("%d%d",&a,&b);
		num[a]++;
		num[b]++;
		if(num[a]==3)cnt++;
		if(num[b]==3)cnt++;
		if(a==b)cnt--;
		if(num[a]>3)f=0;
		if(num[b]>3)f=0;
	}
	if(f)
	cout<<n-cnt<<endl;
	else cout<<0<<endl;
	return 0;
}

G. Period

题意：

给一个字符串，修改m次，问每次的周期。

题解：

周期可以想象成是自己（s1）和自己（s2）比较，s1从最后一个字符开前移，如果能使得s1前面部分的字符串和s2全部字符相同的话，那么它就是肯定满足周期。也可以说是前缀等于后缀。
其实这就是kmp算法。
用kmp算法求next，然后从n开始顺着往前找，每一处都是一个允许的周期。
这也是求nextval的过程。

对于每组查询，在x位置放一个#号，那么只有可能满足在#号之前的匹配了（s2）。
但是p-1（s1）和n-p（s2）不能重合，所以要取min。

注意next不能作为数组名用，c++内部应该已经用了qwq，CE。

#include 
using namespace std;
#define ll long long
const int maxn=1e6+3;
#define sc scanf
#define pr printf 
string s;
int n,m;
int nxt[maxn];
int ans[maxn];
void getnext(){//求next数组 
	nxt[0]=-1;
	int i=0,j=-1;
	while(i<=n){
		if(j==-1||s[i]==s[j]){
			i++;
			j++;
			nxt[i]=j;
		}
		else j=nxt[j];
	}
}
void prenext(){//倒着往前找 
	int now =nxt[n];
	while(now){
		ans[now]++;
		now=nxt[now]; 
	} 
	//求前缀和
	for(int i=1;i<=n;i++)ans[i]+=ans[i-1];
}
int main() {
    cin>>s;n=s.size();
    getnext();prenext();
    cin>>m;
    while(m--){
    	int x;sc("%d",&x);
    	pr("%d\n",ans[min(x-1,n-x)]);
	}
	return 0;
}

G - Desserts

题意：
k种糖果，分给i组，每组最多拿一个，要求糖果必须分完。问1-m组每次多少种分发。

题解：
容易看出每次是C（n，m）的求和，n是组数，m是糖果数。
可以记录m，相同的m每次只算一次然后快速幂。用set存储，p数组记录次数。
快速幂求逆元。阶乘和逆元都记录下来。

#include 
using namespace std;
#define ll long long
const int maxn=1e5+7;
#define sc scanf
#define pr printf 
ll a[maxn];
ll k[maxn];
#define mod 998244353
int n,m;
//快速幂 
ll fpow(ll aa, ll b) {
    ll res = 1;
    while (b) {
        if (b & 1) res = res * aa % mod;
        b >>= 1;
        aa = aa * aa % mod;
    }
    return res;
}

ll inv(ll x) {  return fpow(x, mod - 2);}
ll ny[maxn];
//预处理 
void init (){
	k[0]=0;
	k[1]=1;
	for(int i=2;i<maxn;i++){
		k[i]=k[i-1]*i%mod;
	}
	//逆元
	ny[100000]=inv(k[100000]);
	for(int i=100000-1;i>=0;i--)
	ny[i]=ny[i+1]*(i+1)%mod;
	 
	
}
ll CC(ll i,ll j){
	if(j>i)return 0;
	return k[i]*ny[j]%mod*ny[i-j]%mod;
	//return k[i]/(k[j]*k[i-j]%mod);
}
set<ll>ans;
ll p[maxn];
int main() {
	cin>>n>>m;
	init();
	for(int i=1;i<=n;i++){
	sc("%d",&a[i]);
	p[a[i]]++;
	ans.insert(a[i]);
	}
	for(int i=1;i<=m;i++){
		ll sum=1;
		for (set<ll>::iterator it = ans.begin(); it != ans.end(); it++){
			//ll kk=*it;
			//ll cc=CC(i,kk);
			sum=sum*fpow(CC(i,*it),p[*it])%mod;
		}
		pr("%lld\n",sum);
	}
	//cout<<"--"<
	//cout<<"--"<
	return 0;
}

J .Circular Billiard Table

题意：
射入后反弹多少下回到入射点。（要求第一次）

题解：
推公式——
可以推出圆心角=2倍的入射角。
射出的时候，肯定是转了k个360度，则有：n入射角=k360
可以化为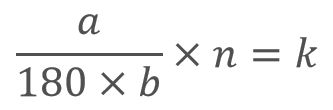
第一次，那么让k最小。

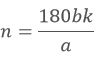
即可变为：
n=180b/gcd（180b，a）
碰撞次数，边减去1，即n-1。

#include 
using namespace std;
#define ll long long
const int maxn=1e5+7;
#define sc scanf
#define pr printf 

int main() {
	int t;cin>>t;
	while(t--){
		ll a,b;
		cin>>a>>b;
		cout<<180*b/__gcd(180*b,a)-1<<endl;
	}
	return 0;
}