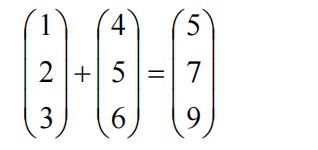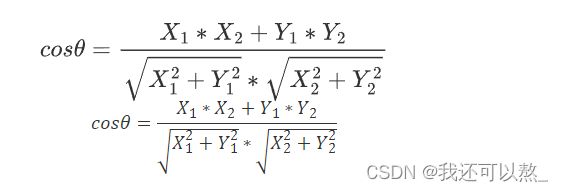线性代数基础--向量

目录

向量的概念

基本概念

抽象概念

向量的意义 

几何意义

物理意义

欧式空间

特点和性质

 行向量与列向量

行向量

列向量

两者的关系

向量的基本运算与范数

向量的基本运算

向量的加法

数乘运算（实数与向量相乘）

转置

向量的范数

向量的模与内积

向量的模

向量的内积（点乘） 

向量的应用——余弦相似度 

---

向量的概念

 

基本概念

向量是线性代数里面最基本的概念，表示的是一组有序的数，它可以表示大小和方向

X = (X~1~,X~2~,...X~n~)

和向量相对应，⼀个数字，称为标量

抽象概念

除了在几何中的直观表示，向量也可以被抽象地定义为具有一定代数性质的数学对象。向量可以用一组有序的实数或复数分量表示，具有加法和数乘等运算规则。

向量的意义 

几何意义

向量可以用来表示具有大小和方向的物理量，例如位移、速度、加速度、力等。在几何上，向量可以表示为从一个点到另一个点的有向线段，起点和终点分别代表向量的位置。

物理意义

1. 位移向量：位移向量用于描述物体从一个位置到另一个位置的位移，包括大小和方向。它可以表示为从起始点到终点的有向线段，描述物体在空间中的移动。

2. 速度向量：速度向量表示物体在某一时刻的速度，包括大小和方向。它是位移向量关于时间的导数，描述物体的位置变化率。

3. 加速度向量：加速度向量表示物体在某一时刻的加速度，包括大小和方向。它是速度向量关于时间的导数，描述物体速度的变化率。

4. 力向量：力向量表示作用在物体上的力，包括大小和方向。根据牛顿第二定律，物体的加速度与作用在物体上的力成正比，方向与力的方向一致。力向量可以用于计算物体的运动和相互作用。

5. 磁场和电场向量：在电磁学中，磁场和电场都可以用向量来表示。磁场向量和电场向量描述了磁场和电场的强度和方向，在电磁相互作用和电磁波传播等现象中起着重要作用。

6. 力矩向量：力矩向量表示施加在物体上的力矩，包括大小和方向。力矩描述了物体绕某一轴旋转的趋势，与施加力的位置和方向有关。

7. 矢量场：矢量场是指在空间中每一点都有一个关联的向量。例如，速度场和电场就是矢量场的示例，它们在空间中的每一点都有一个速度向量或电场向量。

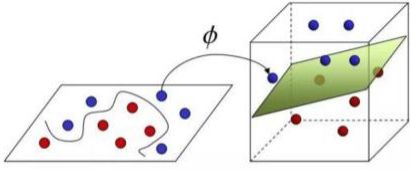
欧式空间

n 维向量集合的全体就构成了 n 维欧式空间，R^n^

例如，所有二维向量构成了二维欧氏空间；所有三维向量构成了三维欧氏空间。

特点和性质

1. 维度：欧氏空间可以是任意维度的，包括一维、二维、三维，甚至更高维度。在二维空间中，我们通常使用平面几何来描述，而在三维空间中，我们使用立体几何来描述。

2. 度量：欧氏空间具有欧几里得度量，即通过距离来度量空间中点之间的间隔。在二维和三维空间中，欧几里得距离可以使用勾股定理计算，即两点之间的直线距离。在n维欧氏空间中，欧几里得距离可以表示为点之间坐标差的平方和的平方根。

3. 坐标系：欧氏空间可以使用坐标系来表示点的位置。在二维空间中，常用笛卡尔坐标系，其中通过两个垂直的坐标轴来确定点的位置。在三维空间中，使用三个相互垂直的坐标轴来表示点的位置。

4. 向量：欧氏空间中的向量具有大小和方向，用于表示物理量和几何对象。向量的加法、减法和数乘操作可以在欧氏空间中定义，使得向量成为对空间中点之间关系的有效描述工具。

5. 内积：欧氏空间中的向量可以进行内积运算。内积是两个向量之间的一种运算，可以用于度量向量之间的夹角和长度。在二维空间中，内积可以通过向量的坐标乘积求和来计算。

 行向量与列向量

行向量

行向量是指由一组有序的数按水平排列而成的向量，其形状为 1 × n。行向量中的元素按从左到右的顺序排列。例如，行向量 [a₁, a₂, ..., aₙ] 可以表示为：

[ a₁ a₂ ... aₙ ]

行向量可以通过将元素按顺序排列在方括号内表示。

列向量

列向量是指由一组有序的数按垂直排列而成的向量，其形状为 n × 1。列向量中的元素按从上到下的顺序排列。例如，列向量 [a₁, a₂, ..., aₙ] 可以表示为：

[ a₁ ] [ a₂ ] [ ... ] [ aₙ ]

列向量可以通过将元素按顺序排列在方括号内，并以换行符分隔表示。

两者的关系

行向量与列向量没有本质的区别 只是表现形式不同

行向量是按行把向量排开，列向量是按列把向量排开

 在数学中我们更多的把数据写成列向量

向量的基本运算与范数

向量的基本运算

• 向量的加法

  就是它们的分量分别相加，显然两个向量的长度得是相等的

同理，向量的减法就是它们的分量分别相减

• 数乘运算（实数与向量相乘）

  使用实数和这个向量的每个数据分别相乘

  

• 转置

  把列向量变成行向量，把行向量变成列向量

向量的范数

范数的公式是向量每个分量绝对值p次方求和，再用幂函数计算p分之一

向量的范数就是把向量变成一个标量，范数的表示就是两个竖线来表示，然后右下角写上p

• 范数公式：

• 1范数L1

  

• 2范数L2

  

向量的模与内积

向量的模

向量的长度叫做向量的模，用两个竖线包起来的向量就代表向量的模，例如：||a||

对于一个n维向量，它的模为：

向量的内积（点乘） 

两个向量的内积（点乘）等于对应位置相乘再相加

两个向量的内积的本质是变成一个标量

向量的应用——余弦相似度 

使用两向量夹角θ的余弦值cosθ来表示两个向量的相似度，称为余弦相似度。余弦相似

度的范围是：[-1,1]，夹角越小，余弦值越接近于1，两个向量越靠近，两者越相似。两个向

量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两

个向量指向完全相反的方向时，余弦相似度的值为-1。

余弦相似度公式为：

 

其中，表示的是向量a和向量b的内积，||a||和||b||分别表示向量a和向量b的模（长度）。

例如，向量a=(X~1~,Y~1~)，向量b=(X~2~,Y~2~)，代入余弦相似度公式可以得到：

可以将其推广至n维向量空间：

若向量a=(X~1~,X~2~,X~3~,...,X~n~)，向量b=(Y1,Y2,Y3,...,Yn)，其夹角的余弦值（余弦相似度）可

以表示为：