刘二大人Pytorch课程笔记
Lecture01. Overview
没啥好记的，理解就好
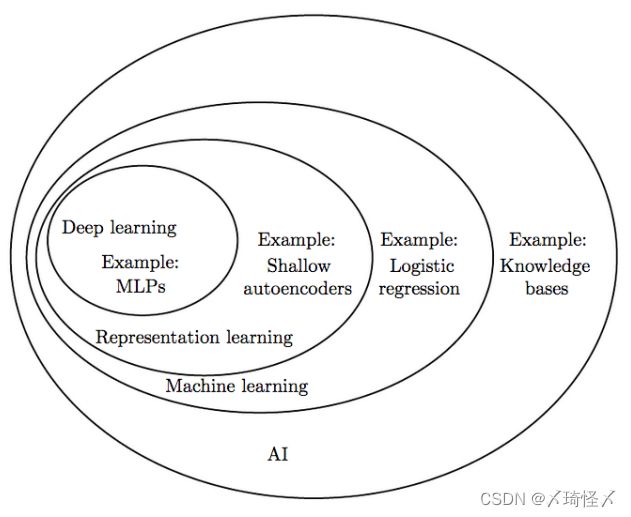
人工智能和机器学习等的关系：
正向传播
正向传播本质上是按照输入层到输出层的顺序，求解并保存网络中的中间变量本身。
反向传播
反向传播本质上是按照输出层到输入层的顺序，求解并保存网络中的中间变量以及其他参数的导数（梯度）。
两者核心都是计算图
正向传播上图中的实际计算过程为
e = ( a + b ) ∗ ( b + 1 ) e=(a+b)*(b+1) e=(a+b)∗(b+1)
每一步都只能进行原子计算，每个原子计算构成一个圈，继而形成整个计算图。
在计算图中，先进行正向计算 c = a + b c=a+b c=a+b, d = b + 1 d=b+1 d=b+1,再进行 e = c ∗ d e=c*d e=c∗d，求解得到 e e e的值以后即完成了正向计算的过程。
在前馈计算过程中，就可以求解得
∂ c ∂ a ∂ c ∂ b ∂ d ∂ b ∂ d ∂ 1 \frac{\partial c}{\partial a} \frac{\partial c}{\partial b} \frac{\partial d}{\partial b} \frac{\partial d}{\partial 1} ∂a∂c∂b∂c∂b∂d∂1∂d
等一系列梯度，这其中所有的梯度信息在正向计算过程中进行保存，并在之后依照计算图中的链接，根据链式法则反方向求导计算 ∂ e ∂ a \frac{\partial e}{\partial a} ∂a∂e以及 ∂ e ∂ b \frac{\partial e}{\partial b} ∂b∂e（需要优化的核心梯度），反方向求导即为反向传播过程。
Lecture02. Linear Model
进行深度学习时的准备过程
- 准备数据集
- 训练集
- 测试集
- 验证集
- 选择模型
- 模型训练
- 进行推理预测
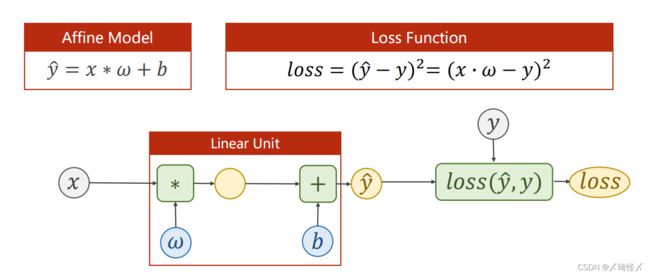
线性模型的基本模型 y ^ = ω x + b \widehat y=\omega x+b y =ωx+b
其中的 ω \omega ω和 b b b是模型中的参数，训练模型的过程即为确定模型中参数的过程
在本模型中设置成 y ^ = ω x \widehat y=\omega x y =ωx
对于不同的 ω \omega ω有不同的线性模型及图像与之对应。
计算训练损失：Training Loss针对一个样本
Mean Square Error（MSE平均平方误差）针对整个训练集
c o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 cost = \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 cost=N1n=1∑N(y n−yn)2
import numpy as np
import matplotlib.pyplot as plt #绘图
x_data = [1.0, 2.0, 3.0] #数据集
y_data = [2.0, 4.0, 6.0]
#前馈计算
def forward(x):
return x * w
#计算损失
def loss(x, y):
y_pred = forward(x)
return (y_pred-y)*(y_pred-y)
w_list = [] #计算权重
mse_list = [] #对应权重损失值
#从0.0一直到4.1以0.1为间隔进行w的取样
for w in np.arange(0.0,4.1,0.1):
print("w=", w)
l_sum = 0
for x_val,y_val in zip(x_data,y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val,y_val)
l_sum += loss_val
print('\t',x_val,y_val,y_pred_val,loss_val)
print("MSE=",l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
#绘图
plt.plot(w_list,mse_list)
plt.ylabel("Loss")
plt.xlabel('w')
plt.show()
运行结果
Lecture03. Gradient Descent
在线性模型中采用了穷举法，但是对于数据集较大的时候穷举不可行，因此提出梯度下降进行优化。
随机选取一个点，计算梯度，并朝着函数值下降最快的方向走，并且更新w值
取值点需要向下更新，所取的梯度即为 ∂ c o s t ∂ ω \frac{\partial cost}{\partial \omega} ∂ω∂cost,更新的公式为
ω = ω − α ∂ c o s t ∂ ω \omega = \omega - \alpha \frac{\partial cost}{\partial \omega} ω=ω−α∂ω∂cost
其中 α \alpha α为学习率即所下降的步长，不宜取太大。
局限性
梯度下降算法容易进入局部最优解（非凸函数）
但是实际问题中的局部最优点较少，或已经基本可以当成全局最优点
梯度下降算法容易陷入鞍点
梯度下降公式推导
由上篇
c o s t = 1 N ∑ n = 1 N ( y ^ n − y n ) 2 cost = \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 cost=N1n=1∑N(y n−yn)2
可知
∂ c o s t ( w ) ∂ ω = ∂ ∂ w 1 N ∑ n = 1 N ( y ^ n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} = \frac{\partial}{\partial w} \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\widehat y_n-y_n)^2 ∂ω∂cost(w)=∂w∂N1n=1∑N(y n−yn)2
其中
y ^ = ω x \widehat y = \omega x y =ωx
则
∂ c o s t ( w ) ∂ ω = ∂ ∂ w 1 N ∑ n = 1 N ( ω x n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} = \frac{\partial}{\partial w} \frac{1}{N} \displaystyle\sum_{n=1}^{N}(\omega x_n-y_n)^2 ∂ω∂cost(w)=∂w∂N1n=1∑N(ωxn−yn)2
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N ∂ ∂ w ( ω x n − y n ) 2 \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}\frac{\partial}{\partial w}(\omega x_n-y_n)^2 ∂ω∂cost(w)=N1n=1∑N∂w∂(ωxn−yn)2
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N 2 ( x n ω − y n ) ∂ ( x n ω − y n ) ∂ w \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}2(x_n \omega-y_n)\frac{\partial(x_n \omega - y_n)}{\partial w} ∂ω∂cost(w)=N1n=1∑N2(xnω−yn)∂w∂(xnω−yn)
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N 2 x n ( x n ω − y n ) \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}2 x_n(x_n \omega - y_n) ∂ω∂cost(w)=N1n=1∑N2xn(xnω−yn)
即
ω = ω − α 1 N ∑ n = 1 N 2 x n ( x n ω − y n ) \omega = \omega - \alpha \frac{1}{N} \displaystyle\sum_{n=1}^{N}2 x_n(x_n \omega - y_n) ω=ω−αN1n=1∑N2xn(xnω−yn)
代码：
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
return x * w
#求MSE
def cost(xs, ys):
cost = 0
for x, y in zip(xs,ys):
y_pred = forward(x)
cost += (y_pred-y) ** 2
return cost/len(xs)
#求梯度
def gradient(xs, ys):
grad = 0
for x, y in zip(xs,ys):
temp = forward(x)
grad += 2*x*(temp-y)
return grad / len(xs)
for epoch in range(100):
cost_val = cost(x_data, y_data)
_cost.append(cost_val)
grad_val = gradient(x_data, y_data)
w -= 0.01*grad_val
print("Epoch: ",epoch, "w = ",w ,"loss = ", cost_val)
print("Predict(after training)",4,forward(4))
#绘图
plt.plot(_cost,range(100))
plt.ylabel("Cost")
plt.xlabel('Epoch')
plt.show()
损失输出结果
随机梯度下降
随机选单个样本的损失为标准
即原公式变为
ω = ω − α ∂ l o s s ∂ ω \omega = \omega - \alpha \frac{\partial loss}{\partial \omega} ω=ω−α∂ω∂loss
其中
∂ l o s s n ∂ ω = 2 x n ( x n ω − y n ) \frac{\partial loss_n}{\partial \omega} = 2 x_n(x_n \omega - y_n) ∂ω∂lossn=2xn(xnω−yn)
对比梯度下降公式为：
∂ c o s t ( w ) ∂ ω = 1 N ∑ n = 1 N 2 x n ( x n ω − y n ) \frac{\partial cost(w)}{\partial \omega} =\frac{1}{N} \displaystyle\sum_{n=1}^{N}2 x_n(x_n \omega - y_n) ∂ω∂cost(w)=N1n=1∑N2xn(xnω−yn)
随机梯度下降的优点：有可能跨越鞍点（神经网络常用）
SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。
这里的随机是指每次迭代过程中，样本都要被随机打乱，打乱是有效减小样本之间造成的参数更新抵消问题。
对梯度下降和随机梯度下降综合一下获取更好的性能
对数据进行分组mini-batch
：组内梯度下降，组间随机梯度下降
代码：
#随机梯度下降
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
return x * w
#求单个loss
def loss(x, y):
y_pred = forward(x)
return (y_pred-y) ** 2
#求梯度 和梯度下降不同之处
def gradient(x, y):
return 2*x*(x*w-y)
print("Predict(after training)",4,forward(4))
for epoch in range(100):
for x, y in zip(x_data,y_data):
grad=gradient(x,y)
w -= 0.01*grad
print("\tgrad: ",x,y,grad)
l = loss(x,y)
print("progress: ",epoch,"w=",w,"loss=",l)
print("Predict(after training)",4,forward(4))
在前面的阐述中，普通的梯度下降算法利用数据整体，不容易避免鞍点，算法性能上欠佳，但算法效率高。随机梯度下降需要利用每个的单个数据，虽然算法性能上良好，但计算过程环环相扣无法将样本抽离开并行运算，因此算法效率低，时间复杂度高。
综上可采取一种折中的方法，即批量梯度下降方法。
将若干个样本分为一组，记录一组的梯度用以代替随机梯度下降中的单个样本。
该方法最为常用，也是默认接口
Mini-Batch
full batch ：在梯度下降中需要对所有样本进行处理过后然后走一步，如果样本规模的特别大的话效率就会比较低。假如有500万，甚至5000万个样本(业务场景中，一般有几千万行，有些大数据有10亿行)的话走一轮迭代就会非常的耗时。
为了提高效率，我们可以把样本分成等量的子集。 例如我们把100万样本分成1000份， 每份1000个样本， 这些子集就称为mini batch。mini-batch的大小一般取2的n次方，然后我们分别用一个for循环遍历这1000个子集。 针对每一个子集做一次梯度下降。 然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。 我们将遍历一次所有样本的行为叫做一个 epoch，（epoch（时代）指的是模型在整个训练数据集上的一次完整迭代。也就是说，一个epoch等价于将所有训练数据都输入到模型中进行一次前向传播和反向传播，并对模型参数进行一次更新）。 在mini batch下的梯度下降中做的事情其实跟full batch一样，只不过我们训练的数据不再是所有的样本，而是一个个的子集。 这样在mini batch我们在一个epoch中就能进行1000次的梯度下降，而在full batch中只有一次。 这样就大大的提高了我们算法的运行速度。
Lecture04. Back Propagation
在前篇的线性模型中
y ^ = ω x \widehat y = \omega x y =ωx
如果以神经网络的视角代入来看，则 x x x为输入层，即input层， ω \omega ω为权重， y ^ \widehat y y 为输出层。在神经网络中，通常将 ω \omega ω以及 ∗ * ∗计算操作的部分合并看做一个神经元（层）。而神经网络的训练过程即为更新 ω \omega ω的过程，其更新的情况依赖于 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss,而并非 ∂ y ^ ∂ ω \frac{\partial \widehat y}{\partial \omega} ∂ω∂y .
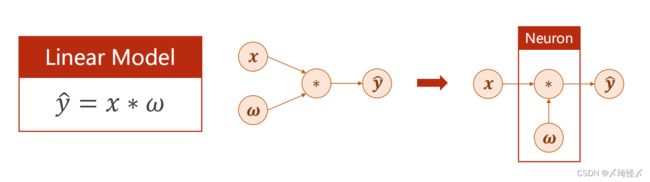
在线性模型中，可以发现这个神经网络进行的运算无论叠加多少层一直都是线性运算，提高层数没有意义
因此为了提高模型的复杂程度，我们为神经网络添加一个非线性因素，例如sigmoid函数
在进行完加法运算以后对这个中间变量进行非线性的变换
添加非线性激活函数
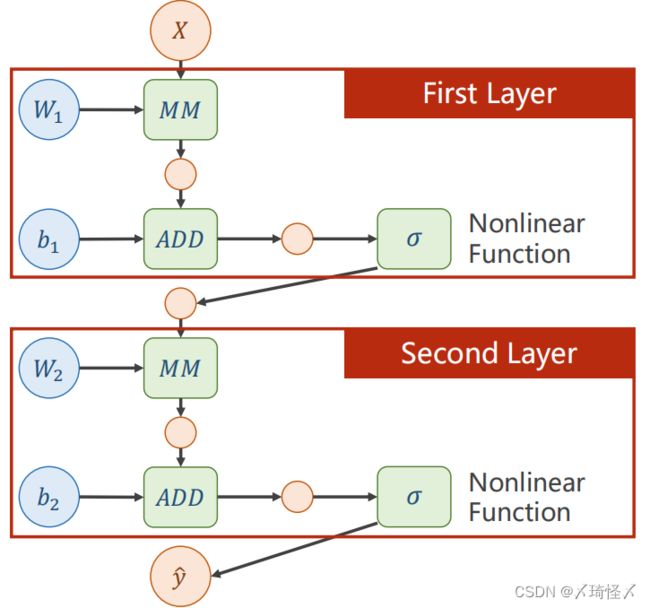
计算图
前馈计算
在某一神经元处，输入的 x x x与 ω \omega ω经过函数 f ( x , ω ) f(x,\omega) f(x,ω)的计算,可以获得输出值 z z z，并继续向前以得到损失值loss.
在向前计算的过程中，在 f ( x , ω ) f(x,\omega) f(x,ω)的计算模块中会计算导数 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z以及 ∂ z ∂ ω \frac{\partial z}{\partial \omega} ∂ω∂z,并将其保存下来（在pytorch中，这样的值保存在变量 x x x以及 ω \omega ω中）。
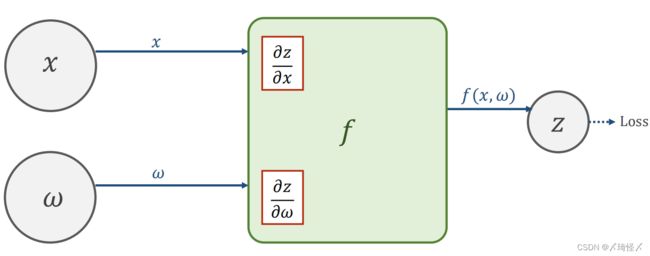
反向传播
即反向求导
由于求导的链式法则,求得loss以后，前面的神经元会将 ∂ l o s s ∂ z \frac{\partial loss}{\partial z} ∂z∂loss的值反向传播给原先的神经元，在计算单元 f ( x , ω ) f(x,\omega) f(x,ω)中,将得到的 ∂ l o s s ∂ x \frac{\partial loss}{\partial x} ∂x∂loss与之前存储的导数相乘，即可得到损失值对于权重以及输入层的导数，即 ∂ l o s s ∂ x \frac{\partial loss}{\partial x} ∂x∂loss,以及 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss.基于该梯度才进行权重的调整。
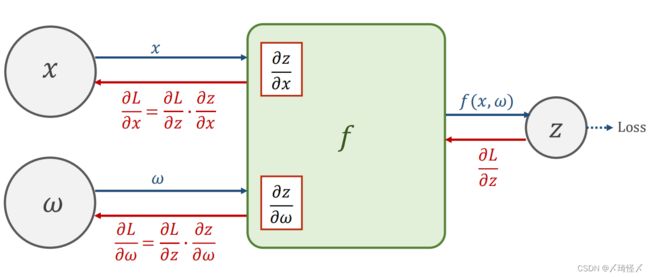
一个简单的计算图例子
Pytorch中的前馈与反馈
Tensor（张量）
Tensor中重要的两个成员，data用于保存权重本身的值 ω \omega ω,grad用于保存损失函数对权重的导数 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss，grad本身也是个张量。对张量进行的计算操作，都是建立计算图的过程。
代码：
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#赋予tensor中的data
w = torch.Tensor([1.0])
#设定需要计算梯度grad
w.requires_grad = True
#模型y=x*w 建立计算图
def forward(x):
'''
w为Tensor类型
x强制转换为Tensor类型
通过这样的方式建立计算图
'''
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print ("predict (before training)", 4, forward(4).item())
for epoch in range(100):
for x,y in zip(x_data,y_data):
#创建新的计算图
l = loss(x,y)
#进行反馈计算，此时才开始求梯度，此后计算图进行释放
l.backward()
#grad.item()取grad中的值变成标量
print('\tgrad:',x, y, w.grad.item())
#单纯的数值计算要利用data，而不能用张量，否则会在内部创建新的计算图
w.data = w.data - 0.01 * w.grad.data
#把权重梯度里的数据清零
w.grad.data.zero_()
print("progress:",epoch, l.item())
print("predict (after training)", 4, forward(4).item())
运算结果
Lecture05. Linear Regression with PyTorch
通常，使用pytorch深度学习有四步
- 准备数据集（Prepare dataset）
- 设计用于计算最终结果的模型（Design model）
- 构造损失函数及优化器（Construct loss and optimizer）
- 设计循环周期（Training cycle）——前馈、反馈、更新
举例：线性模型 - 准备数据集
在原先的题设中， x , y ^ ∈ R x,\widehat y \in R x,y ∈R
在pytorch中，若使用mini-batch的算法，一次性求出一个批量的 y ^ \widehat y y ，则需要 x x x以及 y ^ \widehat y y 作为矩阵参与计算，此时利用其广播机制，可以将原标量参数 ω \omega ω扩写为同维度的矩阵 [ w ] [w] [w],参与运算而不改变其Tensor的性质。
对于矩阵，行表示样本，列表示特征
import torch
#数据作为矩阵参与Tensor计算
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])
- 设计模型
线性单元函数，构造计算图，损失函数。
#固定继承于Module
class LinearModel(torch.nn.Module):
#构造函数初始化
def __init__(self):
#调用父类的init
super(LinearModel, self).__init__()
#Linear对象包括weight(w)以及bias(b)两个成员张量
self.linear = torch.nn.Linear(1,1)
#前馈函数forward，对父类函数中的overwrite
def forward(self, x):
#调用linear中的call()，以利用父类forward()计算wx+b
y_pred = self.linear(x)
return y_pred
#反馈函数backward由module自动根据计算图生成
model = LinearModel()
- 构造损失函数及优化器
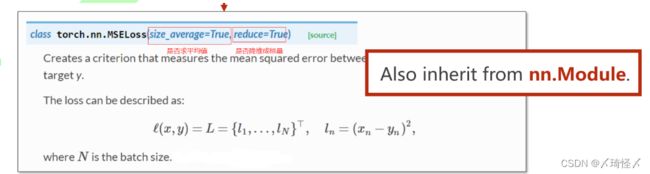
直接调用pytorch中的函数——均方损失函数
criterion = torch.nn.MSELoss(size_average=False)
优化器
#model.parameters()用于检查模型中所能进行优化的张量
#learningrate(lr)表学习率，可以统一也可以不统一
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
- 设计循环周期
模型训练：
- 前馈计算预测值与损失函数
- forward前馈计算预测值即损失loss
- 梯度或前文清零并进行backward
- 更新参数
for epoch in range(100):
#前馈计算y_pred
y_pred = model(x_data)
#前馈计算损失loss
loss = criterion(y_pred,y_data)
#打印调用loss时，会自动调用内部__str__()函数，避免产生计算图
print(epoch,loss)
#梯度清零
optimizer.zero_grad()
#梯度反向传播，计算图清除
loss.backward()
#根据传播的梯度以及学习率更新参数
optimizer.step()
测试模型
#Output
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
#TestModel
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ',y_test.data)
Lecture06. Logistic Regression
逻辑回归和线性回归异同
逻辑回归中因变量是离散的，做分类的。而线性回归中因变量是连续的这是两者最大的区别。因此分类问题中最好使用逻辑回归。
逻辑回归本质是线性回归，但是它加了sigmoid函数
分类问题输出的本质是个概率。
本函数原名为logistics函数，属于sigmod类函数，由于其特性优异，代码中的sigmod函数就指的是本函数。
Logistic 函数
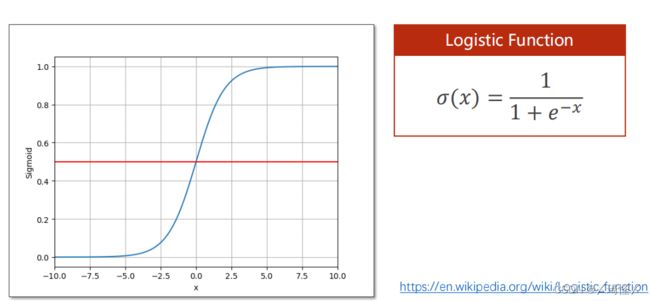
除上述以外，还有其他类的sigmod函数。
Sigmoid函数
线性模型和逻辑回归模型对比：
逻辑回归的损失函数和线性回归损失函数对比：
由于逻辑回归本质也是线性回归，所以利用pytorch解决逻辑回归时参考线性回归的四步。
准备数据集
设计模型
构造损失函数和优化器
训练周期
代码：
import numpy as np
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F #包含了许多函数，sigmoid tanh relu
#准备数据集
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]]) #表示分类，0和1两类
# 设计模型使用的类
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel,self).__init__()
self.linear = torch.nn.Linear(1,1) # linear做线性变换，求wx+b
def forward(self,x):
y_pred = torch.sigmoid(self.linear(x)) #sigmoid函数无参，构造函数里不需要初始化，直接用就可以
return y_pred
model = LogisticRegressionModel()
# 构造损失函数和优化器
criterion = torch.nn.BCELoss(reduction='sum')
# 损失函数有所不同，BCE是二分类交叉熵，MSE是均方误差
# loss是否乘1/N，影响学习率的取值
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
loss_list = []
epoch_list = []
# 训练周期， 前馈, 反向传播, 更新
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
#---------------------------------------#
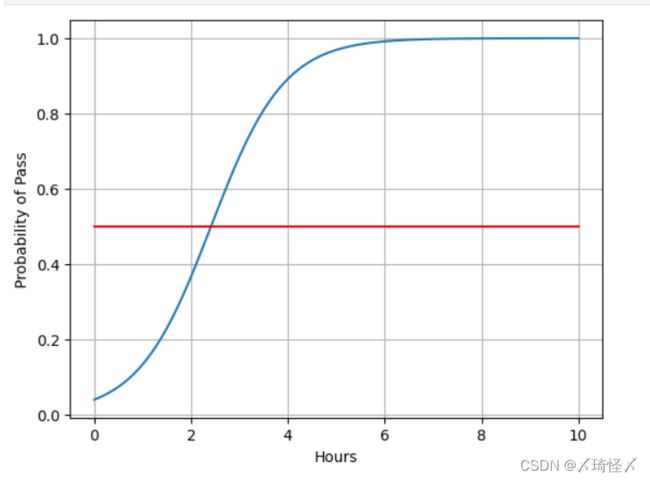
x = np.linspace(0,10,200) # 0-10小时，200个数据点
x_t = torch.Tensor(x).view((200,1)) #200行一列的矩阵
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c = 'r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()
结果：
Lecture07. Multiple Dimension Input
多维特征输入问题
由一维逻辑回归模型过渡到多维：
Mini-Batch
整体上将原先的标量运算，转换为矩阵运算，以方便进行并行计算，提高算法效率。
网络增加
矩阵实质上是用于空间的函数
引入
按照原先的代码思路，只需要将Linear()中的参数改成下面代码，即可完成从8维输入到1位输出的过程。
self.linear = torch.nn.Linear(8,1)
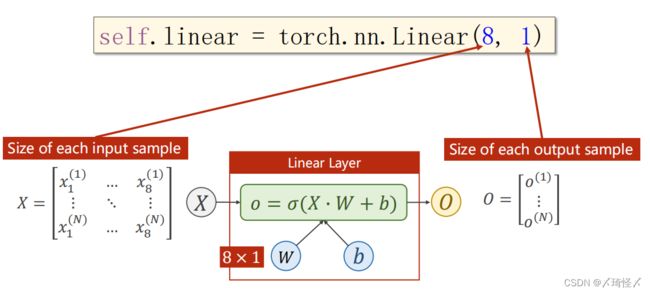
由此，也可以将输出的部分转换为其他维度，来实现分布的维度下降，比如8维转6维，6维转4维，4维转1维，由此可以增加网络层数，增加网络复杂度。同理，对网络结构先增后减也是可以的。
例子：糖尿病预测
import torch
import numpy as np
# 准备数据集
#读取文件，一般GPU只支持32位浮点数
xy = np.loadtxt('diabetes.csv.gz',delimiter=',',dtype=np.float32)
#-1行-1列不取
x_data = torch.from_numpy(xy[:, :-1])
#单取-1列作为矩阵
y_data = torch.from_numpy(xy[:, [-1]])
# 创建模型
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
# 构造损失函数和优化器
criterion = torch.nn.BCELoss(reduction='sum')
# 损失函数有所不同，BCE是二分类交叉熵，MSE是均方误差
# loss是否乘1/N，影响学习率的取值
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)
# 训练周期
epoch_x = []
loss_y = []
for epoch in range(1000):
#Forward 并非mini-batch的设计，只是mini-batch的风格
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch, loss.item())
# 画epoch-loss图，x和y轴的数据
epoch_x.extend([epoch])
loss_y.extend([loss.item()])
#Backward
optimizer.zero_grad()
loss.backward()
#Update
optimizer.step()
# 画图
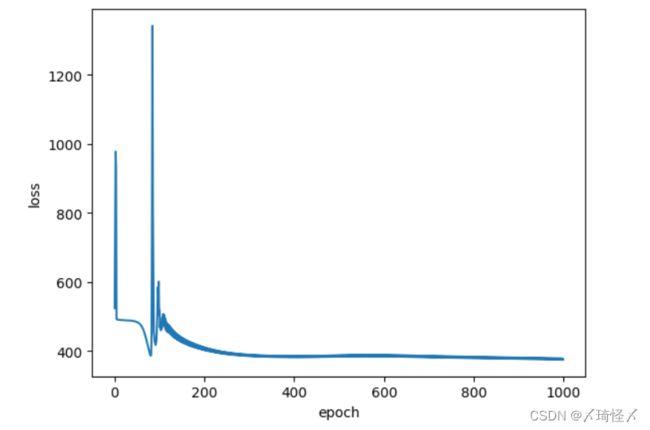
plt.plot(epoch_x, loss_y)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
Lecture08. Dataset and DataLoader
常用术语
Epoch：所有的样本都进行了一次前馈计算和反向传播即为一次epoch
Batch-Size：每次训练的时候所使用的样本数量
Iterations：batch分的次数
DataLoader
核心参数
batch_size,shuffle(洗牌，用于打乱顺序)
核心功能
通过获得DataSet的索引以及数据集大小，来自动得生成小批量训练集
DataLoader先对数据集进行洗牌，再将数据集按照Batch_Size的长度划分为小的Batch，并按照Iterations进行加载，以方便通过循环对每个Batch进行操作
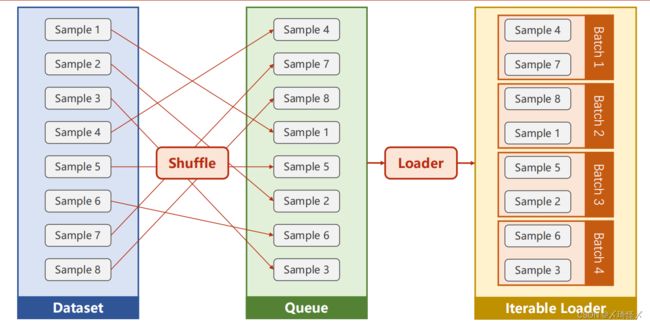
import torch
import numpy as np
#DataSet是抽象类，无法实例化
from torch.utils.data import Dataset
#DataLoader可实例化
from torch.utils.data import DataLoader
class DiabetesDataset(Dataset):
def __init__(self,filepath):
xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
#获得数据集长度
self.len=xy.shape[0]
self.x_data = torch.from_numpy(xy[:, :-1])
self.y_data = torch.from_numpy(xy[:, [-1]])
#获得索引方法
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
#获得数据集长度
def __len__(self):
return self.len
dataset = DiabetesDataset('diabetes.csv')
#num_workers表示多线程的读取
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
if __name__ =='__main__':
for epoch in range(100):
#enumerate:可获得当前迭代的次数
for i,data in enumerate(train_loader,0):
#准备数据dataloader会将按batch_size返回的数据整合成矩阵加载
inputs, labels = data
#前馈
y_pred = model(inputs)
loss = criterion(y_pred, labels)
print(epoch, i, loss.item())
#反向传播
optimizer.zero_grad()
loss.backward()
#更新
optimizer.step()
Lecture09. Softmax Classifier
将多分类的每个输出看成一个二分类用sigmoid解决的话，会导致输出概率相近
因此引入softmax，softmax对概率归一化，使得输出大于0，概率和为1，可以解决抑制问题
假定 Z l Z^l Zl为最后一层线性层的输出, Z i Z_i Zi为第i类的输出。则最终的softmax层函数应为
P ( y = i ) = e z i ∑ j = 0 K − 1 e z i , i ∈ { 0 , ⋯ , K − 1 } P(y=i)=\frac{e^{z_i}}{\sum_{j=0}^{K-1}e^{z_i}}, i \in \{0,{\cdots},K-1\} P(y=i)=∑j=0K−1eziezi,i∈{0,⋯,K−1}
Loss
依照前篇所提及的交叉熵相关理论可知，交叉熵的计算公式如下
H ( P , Q ) = − ∑ i = 1 n P ( X i ) l o g ( Q ( X i ) ) H(P,Q) =-\sum^n_{i=1} P(X_i)log(Q(X_i)) H(P,Q)=−i=1∑nP(Xi)log(Q(Xi))
在多分类问题中，该公式可扩展为
H ( P , Q ) = − ∑ i = 1 n ∑ j = 1 m P ( X i j ) l o g ( Q ( X i j ) ) H(P,Q) =-\sum^n_{i=1}\sum^m_{j=1} P(X_{ij})log(Q(X_{ij})) H(P,Q)=−i=1∑nj=1∑mP(Xij)log(Q(Xij))
其中各个符号含义如下
| 符号 | 含义 |
|---|---|
| m m m | 类别数量 |
| n n n | 样本数量 |
| P ( X i j ) P(X_{ij}) P(Xij) | 指示变量，预测样本 i i i的结果与实际结果 j j j相同取1反之取0 |
| Q ( X i j ) Q(X_{ij}) Q(Xij) | 对于观测样本 i i i预测值为 j j j的概率 |
由于上述计算过程中 P ( X i j ) P(X_{ij}) P(Xij)非0即1，且有且只能有一个1，因此一个样本所有分类的loss计算过程可以简化为
L o s s = − l o g ( P ( X ) ) = − Y l o g Y ^ Loss = -log(P(X)) = -Ylog \widehat Y Loss=−log(P(X))=−YlogY
import torch
import matplotlib.pyplot as plt
from torchvision import transforms # 针对图像处理
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F #使用ReLU
import torch.optim as optim # 优化器
# 1.数据集准备
batch_size = 64
# transform pytorch读图像时，神经网络希望输入比较小，
# pillow把图像转化为图像张量，单通道转化为多通道
transform = transforms.Compose([ #compose可以把[]里的数据进行pipline处理
transforms.ToTensor(), # 转化成张量
transforms.Normalize((0.1307,), (0.3081,)) # normalize归一化，(均值，标准差)
])
# transform放到数据集里是为了对第i个数据集直接操作
train_dataset = datasets.MNIST(root='../dataset/mnist',
train=True,
download=True,
transform=transform)
train_loader = DataLoader(train_dataset,
shuffle=True,
batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/',
train=False,
download=True,
transform=transform)
test_loader = DataLoader(test_dataset,
shuffle=False,
batch_size=batch_size)
# 2.构造模型
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
# 如果是x.view(1,-1),表示需要转化成一行的向量，但是不知道多少列，需要电脑计算
x = x.view(-1, 784) # view改变张量的形式，把（N,1,28,28）变成二阶,-1表示0维度的数字不变
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) #最后一层不激活
model = Net()
# 3.损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()# 交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) #用带冲量的
# 4.训练周期+测试集
def train(epoch):
running_loss = 0.0
for batch_size, data in enumerate(train_loader, 0):
inputs, target = data # x，y
optimizer.zero_grad() # 在优化器优化之前，进行权重清零;
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item() # 累计loss
if batch_size % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_size + 1, running_loss / 300))
def test():
correct = 0
total = 0
with torch.no_grad(): # 不需要计算梯度
for data in test_loader:
images, labels = data
outputs = model(images)
# 求每一行最大值的下标，返回最大值，和下标
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0) # batch_size
correct += (predicted == labels).sum().item() # 比较下标与预测值是否接近，求和表示猜对了几个
print('Accuracy on test set: %d %%' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(100):
train(epoch)
test()
Lecture10. Basic CNN
全连接
前篇中的完全由线性层串行而形成的网络层为全连接层，即，对于某一层的每个输出都将作为下一层的输入。即作为下一层而言，每一个输入值和每一个输出值之前都存在权重。
在全连接层中，实际上是把原先空间状态上的信息，转换为了一维的信息，使得原有的空间相对位置所蕴含的信息丢失。
下文仍以MNIST数据集为例。
CNN过程
卷积实际上是把原始图像仍然按照空间的结构来进行保存数据。
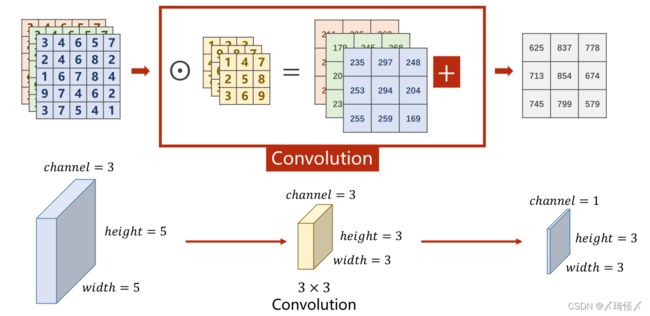
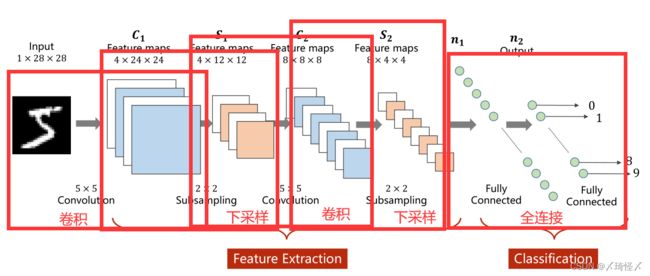卷积过程（Convolution）
1 × 28 × 28 1 \times 28 \times 28 1×28×28指的是 C ( c h a n n l e ) × W ( w i d t h ) × H ( H i g h t ) C(channle) \times W(width) \times H(Hight) C(channle)×W(width)×H(Hight)即通道数 × \times × 图像宽度 × \times × 图像高度，通道可以理解为层数，通过同样大小的多层图像堆叠才形成了最原始的图。
可以抽象的理解成原先的图是一个立方体性质的，卷积是将立方体的长宽高按照新的比例进行重新分割而成的。
如下图所示，底层是一个 3 × W × H 3 \times W \times H 3×W×H的原始图像，卷积的处理是每次对其中一个Patch进行处理，也就是从原数图像的左上角开始依次抽取一个 3 × W ′ × H ′ 3 \times W' \times H' 3×W′×H′的图像对其进行卷积，输出一个 C ′ × W ′ ′ × H ′ ′ C' \times W'' \times H'' C′×W′′×H′′的子图。
下采样过程（Subsampling）
下采样的目的是减少特征图像的数据量，降低运算需求。在下采样过程中，通道数（Channel）保持不变，图像的宽度和高度发生改变
全连接层（Fully Connected）
先将原先多维的卷积结果通过全连接层转为一维的向量，再通过多层全连接层将原向量转变为可供输出的向量。
在前文的卷积过程与下采样过程，实际上是一种特征提取的手段或者过程，真正用于分类的过程是后续的全连接层。
卷积原理
单通道卷积
设定对于规格为 1 × W × H 1 \times W \times H 1×W×H的原图，利用一个规格为 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′的卷积核进行卷积处理的数乘操作。
则需要从原始数据的左上角开始依次选取与核的规格相同( 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′)的输入数据进行数乘操作，并将求得的数值作为一个Output值进行填充。
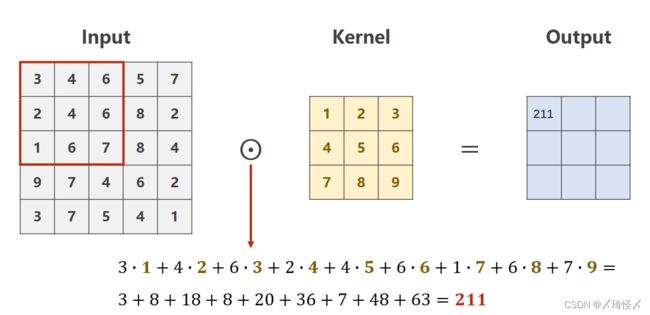
多通道卷积
对于多通道图像( N × W × H N \times W \times H N×W×H)，每一个通道是一个单通道的图像（ 1 × W × H 1 \times W \times H 1×W×H）都要有一个自己的卷积核（ 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′）来进行卷积。
对于分别求出来的矩阵，需要再次进行求和才能得到最后的输出矩阵，最终的输出矩阵仍然是一个 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′的 图像。
平面的图像转为立体的角度即如下图
改进多通道
多通道卷积中，每次只能把 N N N个通道转变为1个通道，而无法在通道这个维度进行增加或降低。
因此，为了对通道进行更加灵活的操作，可以将原先 N × W × H N \times W \times H N×W×H的图像，利用不同的卷积核对其多次求卷积，由于每次求卷积之后的输出图像为 1 × W ′ × H ′ 1 \times W' \times H' 1×W′×H′，若一共求解了 M M M次，即可以将此 M M M次的求解结果按顺序在通道（Channel）这一维度上进行拼接，以此来形成一个规格为 M × W ′ × H ′ M \times W' \times H' M×W′×H′的图像。
总结及代码
每个卷积核的通道数与原通道数一致
卷积核的数量与输出通道数一致
卷积核的大小与图像大小无关
上述中所提到的卷积核，是指的多通道的卷积核，而非前文中提到的二维的。
综上所述为了使下图所表征的过程成立，即若需要使得原本为 n × w i d t h i n × h e i g h t i n n \times width_{in} \times height_{in} n×widthin×heightin的图像转变为一个 m × w i d t h o u t × h e i g h t o u t m \times width_{out} \times height_{out} m×widthout×heightout的图像，可以利用 m m m个大小为 n × k e r n e l _ s i z e w i d t h × k e r n e l _ s i z e h e i g h t n \times kernel\_size_{width} \times kernel\_size_{height} n×kernel_sizewidth×kernel_sizeheight的卷积核。
则在实际操作中，即可抽象为利用一个四维张量作为卷积核，此四维张量的大小为 m × n × k e r n e l _ s i z e w i d t h × k e r n e l _ s i z e h e i g h t m \times n \times kernel\_size_{width} \times kernel\_size_{height} m×n×kernel_sizewidth×kernel_sizeheight
import torch
in_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = 3 #默认转为3*3，最好用奇数正方形
#在pytorch中的数据处理都是通过batch来实现的
#因此对于C*W*H的三个维度图像，在代码中实际上是一个B（batch）*C*W*H的四个维度的图像
batch_size = 1
#生成一个四维的随机数
input = torch.randn(batch_size, in_channels, width, height)
#Conv2d需要设定，输入输出的通道数以及卷积核尺寸
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size)
output = conv_layer(input)
print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)
卷积改进
Padding
若对于一个大小为 N × N N \times N N×N的原图，经过大小为 M × M M \times M M×M的卷积核卷积后，仍然想要得到一个大小为 N × N N \times N N×N的图像，则需要对原图进行Padding，即外围填充。
例如，对于一个 5 × 5 5 \times 5 5×5的原图，若想使用一个 3 × 3 3 \times 3 3×3的卷积核进行卷积，并获得一个同样 5 × 5 5 \times 5 5×5的图像，则需要进行Padding，通常外围填充0
input = [3,4,6,5,7,
2,4,6,8,2,
1,6,7,8,4,
9,7,4,6,2,
3,7,5,4,1]
#将输入变为B*C*W*H
input = torch.Tensor(input).view(1, 1, 5, 5)
#偏置量bias置为false
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)
#将卷积核变为CI*CO*W*H
kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1, 1, 3, 3)
#将做出来的卷积核张量，赋值给卷积运算中的权重（参与卷积计算）
conv_layer.weight.data = kernel.data
output = conv_layer(input)
print(output)
Stride
本质上即是Batch的步长，在Batch进行移动时，每次移动Stride的距离，以此来有效降低图像的宽度与高度。
例如，对于一个 5 × 5 5 \times 5 5×5的原图，若想使用一个 3 × 3 3 \times 3 3×3的卷积核进行卷积，并获得一个 2 × 2 2 \times 2 2×2的图像，则需要进行Stride，且Stride=2
下采样过程
最大池化层（Max Pooling）
对于一个 M × M M \times M M×M图像而言，通过最大池化层可以有效降低其宽度和高度上的数据量，例如通过一个 N × N N \times N N×N的最大池化层，即将原图分为若干个 N × N N \times N N×N大小的子图，并在其中选取最大值填充到输出图中，此时输出图的大小为 M N × M N \frac{M}{N} \times \frac{M}{N} NM×NM 。
import torch
input = [3,4,6,5,
2,4,6,8,
1,6,7,8,
9,7,4,6]
input = torch.Tensor(input).view(1, 1, 4, 4)
#kernel_size=2 则MaxPooling中的Stride也为2
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)
output = maxpooling_layer(input)
print(output)
简单卷积神经网络的实现
模型图
代码
代码图
核心代码
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320, 10)
def forward(self, x):
batch_size = x.size(0)
x = self.pooling(F.relu(self.conv1(x)))
x = self.pooling(F.relu(self.conv2(x)))
x = x.view(batch_size, -1)
x = self.fc(x)
return x
Lecture11. Advanced CNN
GoogLeNet
GoogLeNet包括卷积（Convolution），池化（Pooling）、全连接（Softmax）以及连接（Other）四个部分。
而为了减少代码的冗余，将由以上四个模块所组成的相同的部分，封装成一个类/函数，在GoogLeNet中，这样的部分被称为Inception Module。
Inception Module
实际上Inception Module以及GoogLeNet自身只是一种基础的网络结构，他的出现是为了解决构造网络时的部分超参数难以确定的问题。
以卷积核大小(kernel_size)为例，虽然无法具体确定某问题中所应使用的卷积核的大小。但是往往可以有几种备选方案，因此在这个过程中，可以利用这样的网络结构，来将所有的备选方案进行计算，并在后续计算过程中增大最佳方案的权重，以此来达到确定超参数以及训练网络的目的。
其中的具体成分可以根据问题进行调整，本文中所详细介绍的Inception Module也仅用作参考。
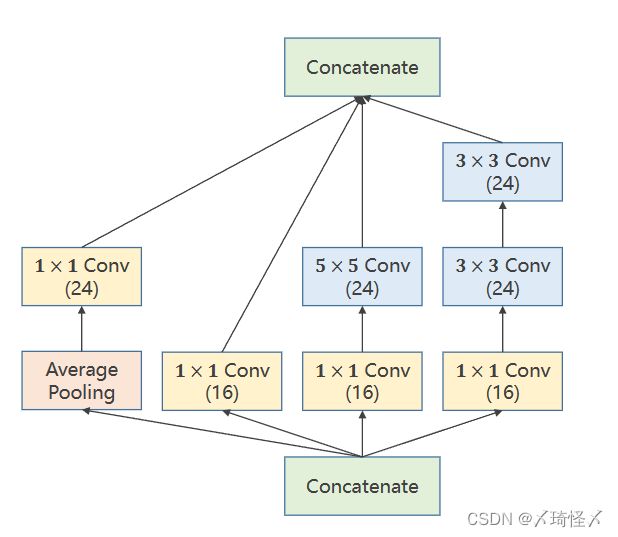
| 模块名称 | 作用 |
|---|---|
| 1 × 1 1 \times 1 1×1 Conv | 其个数与输入张量的通道数相同，用于改变通道数量 |
| 3 × 3 3 \times 3 3×3 Conv | 用于进行 3 × 3 3 \times 3 3×3 卷积 |
| 5 × 5 5 \times 5 5×5 Conv | 用于进行 5 × 5 5 \times 5 5×5 卷积 |
| Average Pooling | 均值池化，需要手动设定padding以及stride来保持图像大小不变 |
| Concatenate | 用于按照某一维度将张量进行拼接 |
在上述四个路径（四种方法）中，最终的输出图必须仍然保持相同的W（图像宽度）以及H（图像高度），不然无法再次进行拼接传输到下一层模块中。
1x1 Conv
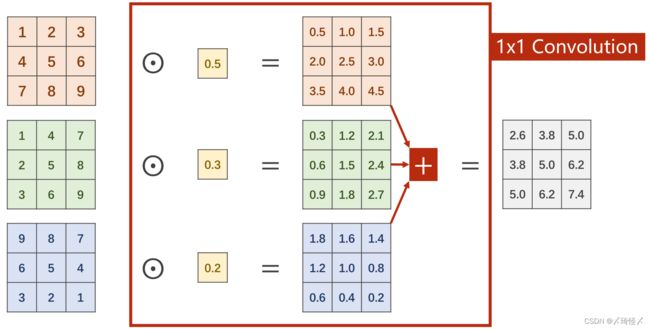
在 1 × 1 1\times1 1×1卷积中，每个通道的每个像素需要与卷积中的权重进行计算，得到每个通道的对应输出，再进行求和得到一个单通道的总输出，以达到信息融合的目的。即将同一像素位置的多个通道信息整合在同位置的单通道上。
若需要得到多通道的总输出，以M个通道为例，则需M组的卷积进行计算再进行堆叠拼接。此处和前篇中的多通道卷积是一样的
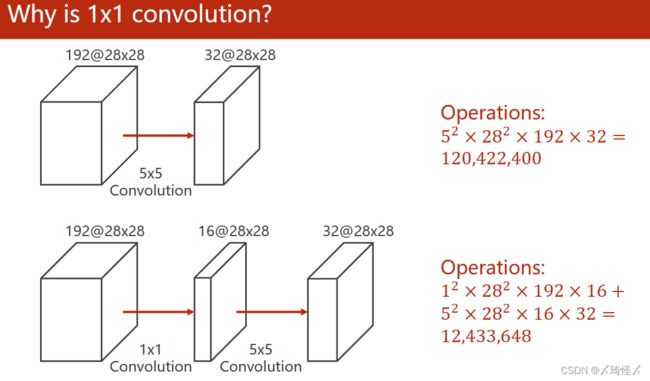
1 X 1卷积可以加速运算
代码实现
路径代码
为了便于代码说明，此处将原Inception Module模块计算图进行了标注，并对模块中的每一个标注进行单独的代码补充，详解写在代码中
其中主要分为两部分，即对于每一条计算路径上的每一个子模块都包括init定义以及forward计算两部分组成。
1、
#init内定义1x1卷积（输入通道 输出通道 卷积核大小）
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
#forward内的方法
#avg_pool2d->均值池化函数 stride以及padding需要手动设置以保持图像的宽度和高度不变
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
#括号内branch_pool的是池化后的结果，括号外的branch_pool是定义的1x1卷积，赋值给对象branch_pool
branch_pool = self.branch_pool(branch_pool)
2、
#init中的定义
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
#将元数据直接用于卷积
branch1x1 = self.branch1x1(x)
3、
#init定义
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
#设置padding是为了保持图像宽高不变
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
#按照计算图的顺序进行forward嵌套运算
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
4、
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
branch3x3 = self.branch5x5_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
Concatenate代码
此时经过计算后，会得到各自通道数目不一但图像大小一致的四组图，再利用Concatenate按通道维度方向进行拼接即可得到输出图像。
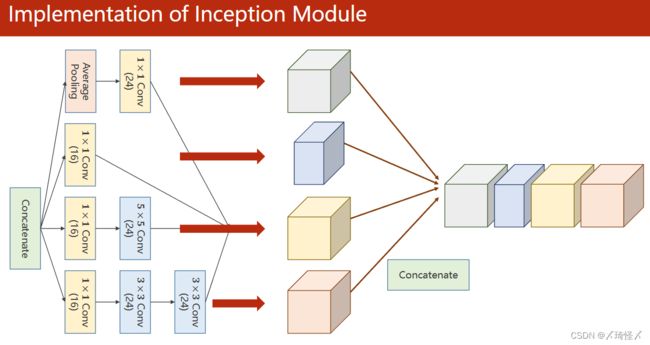
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
#dim=1 意味着按下标为1的维度方向拼接，在图像中即暗指通道（B,C,W,H）
return torch.cat(outputs, dim=1)
整体代码：
class InceptionA(nn.Module):
#仅是一个模块，其中的输入通道数并不能够指明
def __init__(self, in_channels):
super(InceptionA,self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch5x5_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
# 在Inception的定义中，拼接后的输出通道数为24+16+24+24=88个
self.conv2 = nn.Conv2d(88, 20, kernel_size=5)
self.incep1 = InceptionA(in_channels=10)
self.incep2 = InceptionA(in_channels=20)
self.mp = nn.MaxPool2d(2)
#关于1408：
#每次卷积核是5x5，则卷积后原28x28的图像变为24x24的
#再经过最大池化，变为12x12的
#以此类推最终得到4x4的图像，又inception输出通道88，则转为一维后为88x4x4=1408个
self.fc = nn.Linear(1408, 10)
def forward(self,x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
class InceptionA(nn.Module):
#仅是一个模块，其中的输入通道数并不能够指明
def __init__(self, in_channels):
super(InceptionA,self).__init__()
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
def forward(self, x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)
branch3x3 = self.branch5x5_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
# 在Inception的定义中，拼接后的输出通道数为24+16+24+24=88个
self.conv2 = nn.Conv2d(88, 20, kernel_size=5)
self.incep1 = InceptionA(in_channels=10)
self.incep2 = InceptionA(in_channels=20)
self.mp = nn.MaxPool2d(2)
#关于1408：
#每次卷积核是5x5，则卷积后原28x28的图像变为24x24的
#再经过最大池化，变为12x12的
#以此类推最终得到4x4的图像，又inception输出通道88，则转为一维后为88x4x4=1408个
self.fc = nn.Linear(1408, 10)
def forward(self,x):
in_size = x.size(0)
x = F.relu(self.mp(self.conv1(x)))
x = self.incep1(x)
x = F.relu(self.mp(self.conv2(x)))
x = self.incep2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x
ResNet (残差网络)
问题引入
若将某个大小固定的卷积核进行反复迭代，会不会得到更好的结果。
但事实上，以CIFAR-10为例，对于 3 × 3 3 \times 3 3×3的卷积而言，20层的训练效果要优于56层。由图中可以明显看出，在训练集以及测试集中，20层的误差是更小的。
其中最可能的原因是梯度消失问题。
梯度消失
由于在梯度计算的过程中是用的反向传播，所以需要利用链式法则来进行梯度计算，是一个累乘的过程。若每一个地方梯度都是小于1的，即
∂ c o s t ∂ ω < 1 \frac{\partial cost}{\partial \omega} < 1 ∂ω∂cost<1
,则累乘之后的总结果应趋近于0，即
∂ C o s t ∂ Ω → 0 \frac{\partial Cost}{\partial \Omega} \to 0 ∂Ω∂Cost→0
由原先权重更新公式
ω = ω − α ∂ c o s t ∂ ω \omega = \omega - \alpha \frac{\partial cost}{\partial \omega} ω=ω−α∂ω∂cost
可知， ∂ c o s t ∂ ω \frac{\partial cost}{\partial \omega} ∂ω∂cost趋近于0，则 ω \omega ω不会再进行进一步的更新。由于深度学习的网络层数较多，为了解决梯度消失问题，从而产生了ResNet。
与传统神经网络的比较
传统神经网络
在传统神经网络中，先进行权重计算（如卷积，Softmax等），再经过激活函数（如relu等），最终得到输出。
Residual Net
在Residual Net中引入了跳链接，即让输入在N（一般 N = 2 N=2 N=2）层连接后并入第N层的输出，实现如图所示的
H ( x ) = F ( x ) + x H(x) = F(x) + x H(x)=F(x)+x
之后再进行relu激活,以此来得到输出。
在这样的结构中，以图中为例，如果要进行 H ( x ) H(x) H(x)对 x x x的求导，则会有
∂ H ( x ) ∂ x = ∂ F ( x ) ∂ x + 1 \frac{\partial H(x)}{\partial x} = \frac{\partial F(x)}{\partial x} + 1 ∂x∂H(x)=∂x∂F(x)+1
即，若存在梯度消失现象，即存在某一层网络中的 ∂ F ( x ) ∂ x → 0 \frac{\partial F(x)}{\partial x} \to 0 ∂x∂F(x)→0,由于上式存在，则会使得在方向传播过程中，传播的梯度会保持在1左右，即 ∂ H ( x ) ∂ x → 1 \frac{\partial H(x)}{\partial x} \to 1 ∂x∂H(x)→1.如此，离输入较近的层也可以得到充分的训练。
代码实现
Residual Block
由于在ResNet中，跳链接需要实现一个权重层结果与输入相加的操作，则需要保证权重层的输出结果，与输入的维度是相同的。即等宽等高等通道数。
残差块代码
class RsidualBlock(nn.Module):
def __init__(self, in_channels):
super(RsidualBlock, self).__init__()
#保持输出和输入一致
self.channels = in_channels
self.conv1 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)
def forward(self, x):
y = F.relu(self.conv1(x))
#第二层先求和再激活
y = self.conv2(y)
return F.relu(x+y)
结构代码：
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=5)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5)
self.mp - nn.MaxPool2d(2)
self.rblock1 = ResiduleBlock(in_channels=16)
self.rblock2 = ResidualBlock(in_channels=32)
self.fc = nn.Linear(512, 10)
def forward(self,x):
in_size = x.size(0)
x = self.mp(F.relu(self.conv1(x)))
x = self.rblock1(x)
x = self.mp(F.relu(self.conv2(x)))
x = self.rblock2(x)
x = x.view(in_size, -1)
x = self.fc(x)
return x