Java栈和队列

栈

栈是一种特殊的线性表，只允许在固定的一端进行插入和删除操作，即“后进先出”，进行数据插入和删除的一端称为栈顶，另一端则是栈底。

栈的插入操作叫做进栈，压栈，入栈。

栈的删除操作叫做出栈。

栈的使用

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

Stack<Integer> stack = new Stack<>();//创建一个元素为Integer的栈
stack.push(10);
stack.push(20);//放元素，入栈
int x = stack.pop();//出栈
//x = 20
int y = stack.peek()//获取当前栈顶元素，但不删除
//y = 10
boolean ret = stack.empty();
//ret = false

栈的模拟实现

栈的底层是一个数组，当然也可以用链表来实现。

public class MyStack {
    private int[] elem;//用数组实现
    private int usedSize;//元素的个数
    public MyStack() {
        this.elem = new int[5];//分配内存
    }

    public void push(int val) {
        if(isFull()) {
            //判满，如果满了二倍扩容
            elem = Arrays.copyOf(elem, 2 * elem.length);
        }
        elem[usedSize++] = val;
    }

    public boolean isFull() {
        return usedSize == elem.length;
    }
    public int pop() {
        //判断栈不为空
        if(empty()) {
            throw new EmptyException("stack is empty");
        }
        return elem[--usedSize];
        //把元素个数减一就可，下一个数据可以覆盖
    }
    public boolean empty() {
        return usedSize == 0;
    }
    public int pick() {
        if(empty()) {
            throw new EmptyException("stack is empty");
        }
        return elem[usedSize - 1];
    }
}

栈的使用

1. 改变元素的序列

1. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）

​ A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1

A：进1，出1，进2，进3，进4，出4，出3，出2.

B：进1，进2，出2，进3，出3，进4，出4，出1.

C：进1，进2，进3，出3，error

D：进1，进2，进3，出3，进4，出4，出2，出1.

2.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）。

A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA

栈底 ----------->栈顶

1 2 3 4 5 A B C D E

出栈顺序：

E D C B A 5 4 3 2 1

2. 将递归转化为循环

逆序打印链表

// 递归方式
void printList(Node head){
	if(null != head){
		printList(head.next);
		System.out.print(head.val + " ");
	}
}
// 循环方式
void printList(Node head){
	if(null == head){
		return;
	}
    Stack<Node> s = new Stack<>();
    // 将链表中的结点保存在栈中
    Node cur = head;
    while(null != cur){
        s.push(cur);
        cur = cur.next;
    }
        // 将栈中的元素出栈
    while(!s.empty()){
        System.out.print(s.pop().val + " ");
    }
}

3. 括号匹配

( [ ) ] 闭合顺序不对

( ( ) 左括号多

( ) ) 右括号多

我们可以把右括号放入栈中，等到当前括号为左括号时，将它与栈顶元素进行匹配，如果相同，则匹配成功，将栈顶元素弹出。如果不相同，则匹配失败，直接返回false。如果栈空了，而外面还有左括号，则匹配失败，如果栈内有元素，而外面没有左括号了，则匹配失败。

public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(int i = 0; i < s.length(); i++) {
            char str = s.charAt(i);
            if(str == '(' || str == '{' || str == '[') {
                stack.push(str);
            } else {
                if(stack.empty()) {
                    //左括号多
                    return false;
                } else {
                    char str2 = stack.peek();
                    if(str2 == '(' && str == ')' || str2 == '{' && str == '}' || str2 == '[' && str == ']') {
                        stack.pop();
                    } else {//左右括号不匹配
                        return false;
                    }
                }
            }
        }
        if(!stack.empty()) {
            //右括号多了
            return false;
        }
        return true;
    }

4. 逆波兰表达式求值

逆波兰表达式也叫后缀表达式。

常见题型有：

①根据中缀表达式，求后缀表达式

​ 中缀表达式a+b*c+(d*e+f)*g ,将其转化成后缀表达式

方法：先乘除，后加减，加括号

( (a + (b*c)) + ( ( (d*e)+f)*g ) )

​ 然后将运算符放到当前括号的后面（前缀表达式就是放在括号前面）

( (a (b c)*)+ ( ( (d e)*f)+g )* )+

​ 最后去掉括号,得到后缀表达式

a b c* + d e* f + g * +

如果我们将字母赋值

1+2*3+(4*5+6)*7 = 179

那么后缀表达式该如何计算呢？

1 2 3* + 4 5 * 6 + 7 * + = ?

这时，我们就需要借助栈了

如果当前字符是数字的话，我们就直接放进栈内

但如果当前字符是运算符，那么我们就需要从栈中pop出两个数字，第一个放在运算符的右边，第二个放在运算符的左边。将算出来的数再push到栈中。

以此类推

我们就可以得到 ，1 2 3* + 4 5 * 6 + 7 * + =179

这样我们就可以解出这个题了

public boolean isOpera(String x) {
        if(x.equals("+") || x.equals("-") || x.equals("*") || x.equals("/")){
            return true;
        }
        return false;
    }
public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();//实例化一个栈存储数字
        for(String s : tokens) {
            //遍历字符串
            if(!isOpera(s)) {//判断是否为运算符
                //如果不是运算符，就将字符串转化成数字push进栈
                stack.push(Integer.parseInt(s));
            } else {
                //如果是运算符，那么进行相应的运算
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch(s) {
                    case "+" :
                        stack.push(num1 + num2);
                        break;
                    case "-" :
                        stack.push(num1 - num2);
                        break;
                    case "*" :
                        stack.push(num1 * num2);
                        break;
                    case "/" :
                        stack.push(num1 / num2);
                        break;
                }
            }
        }
        return stack.pop();
    }

5. 出栈入栈次序匹配

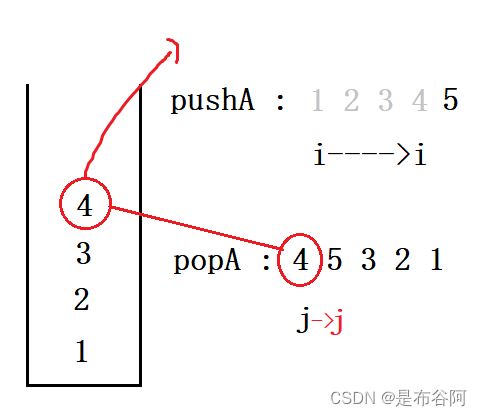
pushA ：1 2 3 4 5

popA ：4 5 3 2 1

用i来遍历pushA，用j来遍历popA，将pushA中的元素放入栈内，直到pushA的元素与 popA的元素匹配，那么将pushA的栈顶元素弹出，ij往后移，以此类推

public boolean IsPopOrder(int [] pushA,int [] popA) {
     Stack<Integer> stack = new Stack<>();
     int j = 0;
     for (int i = 0; i < pushA.length; i++) {
         stack.push(pushA[i]);//每次都入栈
         while(!stack.empty() && j < popA.length && stack.peek() == popA[j]) {
             //判断栈和j，防止越界
             stack.pop();//当栈顶元素与popA[j]相同时，可以出栈
             j++;
         }
     }
     return stack.empty();//如果栈全空了，并且popA也遍历完了，证明匹配成功
 }

6. 最小栈

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

前四个都是比较基础的内容，在上文的栈的模拟实现都实现过，关键是最后一个：获取栈中最小的元素。

栈中的最小值是在随时发生变化的，这个最小值拿的是当前栈中剩下元素的最小值，随着弹出数据，最小值也是发生改变的，类似于更新的最小值倒着往回取。

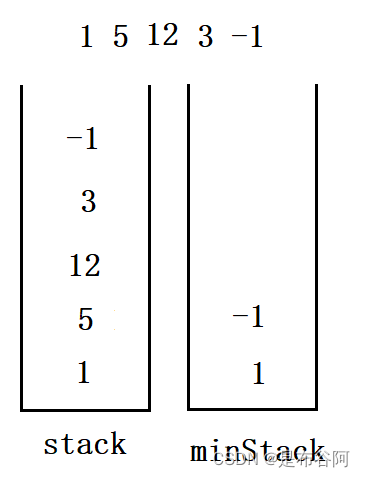
举个例子，在一个栈stack里，我们依次放入了 1 5 12，现在要获取最小元素1，该如何获取呢？此时我们可以再创建一个minStack,放入此刻为止最小的元素。

那么从头开始，stack放入1 ，此刻最小的元素为1，则minStack也放入1，继续放5，与minStack栈顶元素相比，还是1大，所以5不会放入minStack，如果此时我将stack放入-1，与minStack栈顶元素相比，比1小，那么-1就可以放入minStack中，现在minStack中就有了-1，1两个元素。如果当前元素与minStack中的栈顶元素相同，也需要放入。

这样我们就可以轻松的获取当前栈中最小的元素了。

如果要pop stack中的栈顶元素，一定要和minStack的栈顶元素比较，如果相同的话，也需要pop minStack的元素。

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> minstack;

    public MinStack() {
        this.stack = new Stack<>();
        this.minstack = new Stack<>();
    }

    public void push(int val) {
        stack.push(val);
        if(minstack.empty()) {
            //当栈第一次存放数据的时候，两个栈都要存储数据
            minstack.push(val);
        } else {
            if(val <= minstack.peek()) {
                //放入小于等于最小值的元素
                minstack.push(val);
            }
        }
    }

    public void pop() {
        if(stack.empty()) {
            return;
        }
        int n = stack.pop();
        if(n == minstack.peek()) {
            //如果stack要弹出的元素与minstack的栈顶元素相同，那么两个栈都要出
            minstack.pop();
        }
    }

    public int top() {
        if(stack.empty()) {
            return -1;
        } else {
            return stack.peek();
        }
    }

    public int getMin() {
        return minstack.peek();
    }
}

概念区分

栈，虚拟机栈，栈帧有什么区别？

栈是一种数据结构；虚拟机栈是一块内存；栈帧是指函数开辟时在虚拟机栈占用的一块内存。

队列

概念

是一种先进先出的数据结构。有队头和队尾。数据从队尾进从队头出。

这里我们用链表来实现队列。当然也可以用数组来实现。

栈是用数组来实现的，那他可不可以用链表来实现呢？当然也可以。

我们知道用数组来实现的栈，他的入栈和出栈时间复杂度均为O(1),如果用链表能不能做到O(1)？

可以的：如果是双向链表，不管从那边入栈出栈，时间复杂度均是O(1)，LinkedList也经常被当作栈来使用；如果是单链表，可以采用头插法的方式入栈，以删除头节点的方法出栈；

用链表实现队列

如果用双向链表，那么入队和出队都能达到O(1);如果使用单链表并且记录了最后一个结点的位置，那么可以从尾入队，从头出队。如果头进尾出，那么出队的复杂度会达到O(n)。

使用

在Java中，Queue是个接口，底层是通过链表实现的。

方法	功能
boolean offer(E e)	入队列
E poll()	出队列
peek()	获取队头元素
int size()	获取队列中有效元素个数
boolean isEmpty()	检测队列是否为空

注意：Queue是个接口，在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。

public static void main(String[] args) {
    Queue<Integer> q = new LinkedList<>();
    q.offer(1);
    q.offer(2);
    q.offer(3);
    q.offer(4);
    q.offer(5); // 从队尾入队列
    System.out.println(q.size());
    System.out.println(q.peek()); // 获取队头元素
    q.poll();
    System.out.println(q.poll()); // 从队头出队列，并将删除的元素返回
    if(q.isEmpty()){
        System.out.println("队列空");
    }else{
    	System.out.println(q.size());
    }
}

队列的模拟实现

队列中既然可以存储元素，那底层肯定要有能够保存元素的空间，通过前面线性表的学习了解到常见的空间类型有两种：顺序结构 和 链式结构。那么队列的实现使用顺序结构还是链式结构好？

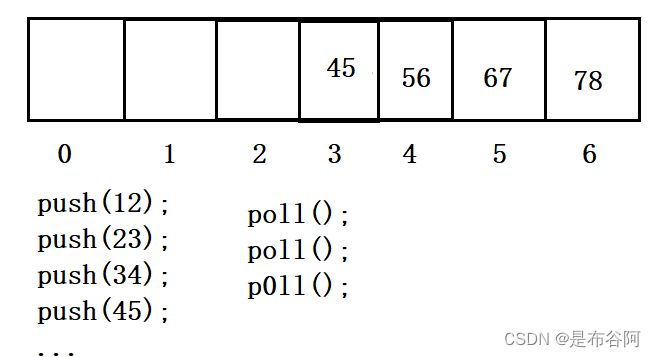
当然是链式结构，如果用顺序结构（数组），那么可能会出现很多空余的内存。

这样一看，队列似乎并没有满，但就是放不下元素了，让空间利用率大大降低，这就是使用顺序表的弊端。

public class MyQueue {
    static class ListNode {
        public int val;
        public ListNode next;
        public ListNode(int val) {
            this.val = val;
        }
    }
    public ListNode head;
    public ListNode last;
    private int usedSize;
    public void offer(int val) {
        ListNode node = new ListNode(val);
        if(head == null) {
            //队列为空
            head = node;
            last = node;
        } else {
            last.next = node;
            last = last.next;
        }
        usedSize++;
    }

    public int poll() {
        if(head == null) {
            //队列为空
            return -1;
        }
        int val = 0;
        val = head.val;
        if(head.next == null) {
            //只有一个元素
            head = null;
            last = null;
            return val;
        }
        //有多个元素
        head = head.next;
        usedSize--;
        return val;
    }
    public int peek() {
        if(head == null) {
            return -1;
        }
        return head.val;
    }
    public int size() {
        return usedSize;
    }
}

循环队列

我们知道如果用顺序表来实现队列的话会浪费空间，但是如果将队首和队尾连接起来，那么队伍的空间就能循环利用起来。

一开始没有数据的时候，front和rear指向同一个空间，当数组满了之后，front和rear依然指向同一个空间，那么到底以什么条件判定队列为空，队列为满呢？

1. 当 front == rear 时，队列为空

2. ①定义一个usedSize，usedSize == len 时，队列为满

②浪费一个空间表示满（以上图为例，当rear指向7下标时，就不能入队了，表示满了）

那么问题又来了，rear和front怎么从7下标走到0下标？(用上面的方法2时)

rear = (rear + 1) % len

front = (front + 1) % len

循环队列的实现

//使用了方法2
class MyCircularQueue {
    private int[] elem;
    private int front;
    private int rear;
    public MyCircularQueue(int k) {
        this.elem = new int[k + 1];
        //因为我们是采用的浪费一个空间的方法，所以我们需要多创建一个空间，才能放得开想放的k个元素，如果不多创建，那么只能放入k-1个元素。
    }
    //入队
    public boolean enQueue(int value) {
        if(isFull()) {
            //满了不加
            return false;
        }
        elem[rear] = value;
        rear = (rear + 1) % elem.length;
        return true;
    }

    public boolean deQueue() {
        if(isEmpty()) {
            return false;
        }
        front = (front + 1) % elem.length;
        //从队头出
        return true;
    }

    public int Front() {
        if(isEmpty()) {
            return -1;
        }
        //获得队头元素
        return elem[front];
    }

    public int Rear() {
        //得到队尾元素
        if (isEmpty()) {
            return -1;
        }
        int index = (rear == 0) ? elem.length - 1 : rear - 1;
        //如果rear == 0，那么就不能直接让index = rear - 1，没有下标是-1的元素，所以直接让index = elem.length - 1即可获得队尾元素。
        return elem[index];
    }

    public boolean isEmpty() {
        return rear == front;
    }

    public boolean isFull() {
        return (rear + 1) % elem.length == front;
    }
}

双端队列(Deque)

双端队列（deque）是指允许两端都可以进行入队和出队操作的队列，deque 是 “double ended queue” 的简称。那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。

它的用途十分的广泛，不仅可以用作队列，还可以用做栈，链表。

public static void main(String[] args) {
    Deque<Integer> queue = new LinkedList<>();//链式队列，双端队列的链式实现
    deque.offer(1);//队列的方法
    Deque<Integer> stack = new LinkedList<>();//链式栈
    stack.push(2);//栈的方法
    Deque<Integer> stack1 = new ArrayDeque<>();//顺序栈，双端队列的线性实现
}

队列和栈的相互实现

1. 队列实现栈

   队列是先进先出，栈是先进后出，如果想用队列来实现栈的话，一个队列肯定是不能完成的，这是需要借助两个队列。

   例如如果我入了12，23这里两个数据，我想拿到23，就可以把12放到另一个队列中，这样就可以拿到23了。

   假如队列里有n个元素，如果要拿栈顶元素，就可以先把n - 1个元素放到另一个队列中。之后再存放数据的时候，哪个队列不为空就放到哪里。

   

   1. push元素时，把元素放到不为空的队列中。
   2. pop的时候，出不为空的队列中的size - 1个元素，剩下的元素就是我们要出栈的元素。

class MyStack {
    private Queue<Integer> queue1;
    private Queue<Integer> queue2;
    public MyStack() {
        this.queue1 = new LinkedList<>();
        this.queue2 = new LinkedList<>();
    }
    
    public void push(int x) {
        if(empty()) {
            //队列都为空的时候默认放到队列1
            queue1.offer(x);
        } else if(!queue1.isEmpty()) {
            queue1.offer(x);
        } else {
            queue2.offer(x);
        }
    }
    
    public int pop() {
        if(empty()) {
            //两个队列都为空，说明没有元素
            return -1;
        } else if(!queue1.isEmpty()) {
            int curSize = queue1.size();
            //把n-1个数据放到空队列里
            //不能这么写：i < queue.size() - 1
            //因为size一直在变化
            for(int i = 0; i < curSize - 1; i++) {
                int x = queue1.poll();
                queue2.offer(x);
            }
            return queue1.poll();
        } else {
            int curSize = queue2.size();
            for(int i = 0; i < curSize - 1; i++) {
                int x = queue2.poll();
                queue1.offer(x);
            }
            return queue2.poll();
        }
    }
    
    public int top() {
        if(empty()) {
            return -1;
        } else if(!queue1.isEmpty()) {
            int curSize = queue1.size();
            int x = 0;
            //把所有的元素都放到空队列中，记录下最后一个元素并返回。
            for(int i = 0; i < curSize; i++) {
                x = queue1.poll();
                queue2.offer(x);
            }
            return x;//最后一个元素返回
        } else {
            int curSize = queue2.size();
            int x = 0;
            for(int i = 0; i < curSize; i++) {
                x = queue2.poll();
                queue1.offer(x);
            }
            return x;
        }
    }
    
    public boolean empty() {
        return queue1.isEmpty() && queue2.isEmpty();
    }
}

2. 栈实现队列

   显然，拿一个栈也不可能能实现队列，所以我们也需要使用两个栈。

   以下图为例，模拟出栈假如我们要出12这个数字，我们可以把12和23全部移到stack2中，然后将栈顶元素12弹出。我们可以让所有的出栈操作都在stack2中完成，如果没有数据了，再将stack1中的数据全部到在stack2中。

   

   模拟入栈 无论stack1是空还是非空，都往stack1里入。

   总结：

   入队 统一入到第一个栈中

   出队 统一在第二个栈出，如果没有元素就将栈1元素倒入栈2，出栈顶元素。

   class MyQueue {
       private Stack<Integer> stack1;
       private Stack<Integer> stack2;
       public MyQueue() {
           stack1 = new Stack<>();
           stack2 = new Stack<>();
       }
       
       public void push(int x) {
           stack1.push(x);
           //所有放在栈1
       }
       
       public int pop() {
           if(stack2.empty()) {
               //如果栈2为空，将栈1元素倒入栈2
               while(!stack1.empty()) {
                   int val = stack1.pop();
                   stack2.push(val);
               }
           }
           return stack2.pop();
       }
       
       public int peek() {
           if(stack2.empty()) {
               while(!stack1.empty()) {
                   int val = stack1.pop();
                   stack2.push(val);
               }
           }
           return stack2.peek();
       }
       
       public boolean empty() {
           return stack1.empty() && stack2.empty();
       }
   }