(转载)PID神经元网络解耦控制算法(matlab实现)

​本博客的完整代码获取：https://www.mathworks.com/academia/books/book106283.html​

1案例背景

1.1PID 神经元网络结构

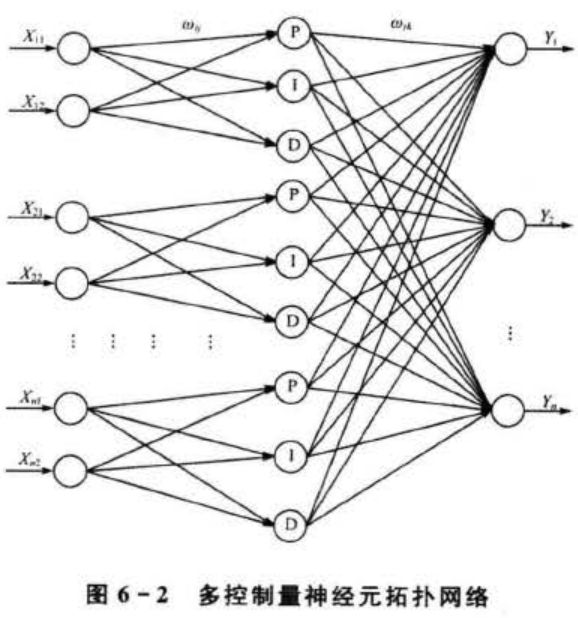
        PID神经元网络从结构上可以分为输人层、隐含层和输出层三层，n个控制量的PID神经元网络包含n个并列的相同子网络,各子网络间既相互独立,又通过网络连接权值相互联系。每个子网络的输入层有两个神经元,分别接收控制量的目标值和当前值。每个子网络的隐含层由比例元,积分元和微分元构成,分别对应着PID控制器中的比例控制,积分控制和微分控制。PID神经元网络按被控系统控制量的个数可以分为控制单变量系统的单控制量神经元网络和控制多变量系统的多控制量神经元网络。其中单控制量神经元网络是PID神经元网络的基本形式,多控制量神经元网络可以看成是多个单控制量神经元网络的组合形式。单控制量神经元网络的拓扑结构如图6-1所示。

1.2控制律计算

        PID神经元网络分为输入层、隐含层和输出层,网络输入量为控制量当前值和控制目标，输出量为控制律,各层输人输出计算公式如下。
        1)输入层

1.3权值修正

        PID神经元网络在控制的过程中根据控制量误差按照梯度修正法修正权值,使得控制量不断接近控制目标值,权值修正的过程如下。
1.4 控制对象

        PID神经元网络的控制对象是一个3输入3输出的复杂耦合系统,系统的传递函数如下:
2 模型建立

        PID神经元网络控制器和被控系统构成的闭环控制系统如图6-3所示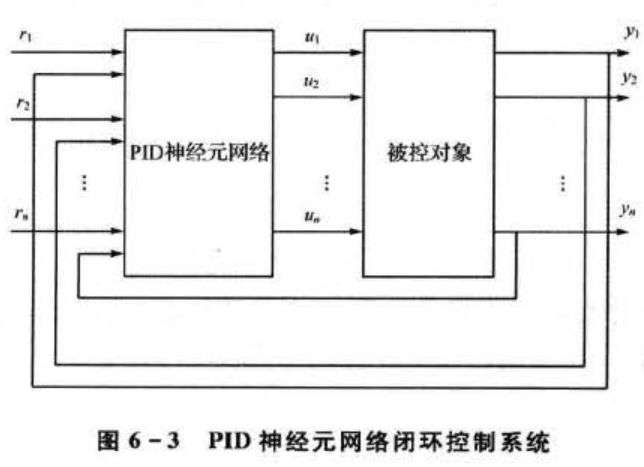
        图中，r1,r2，…,rn是控制量控制目标, u1,u2,…, un为控制器控制律，y1,y2,…,yn为控制量当前值。对于本案例来说,由于被控对象有三个控制量,所以选择包含三个单神经元网络组成的多神经元网络作为系统控制器。网络权值随机初始化,控制量初始值为[0 0 0],控制目标为[0.7 0.4 0.6],控制时间间隔为0.001 s.

3编程实现

        根据PID神经元网络控制器原理,在 MATLAB中编程实现PID神经元网络控制多变量耦合系统。完整matlab代码如下：

%% 该代码为基于PID神经网络的系统控制算法
%% 清空环境变量
clc
clear

%% 网络结构初始化
rate1=0.006;rate2=0.001; %学习率
k=0.3;K=3;
y_1=zeros(3,1);y_2=y_1;y_3=y_2;   %输出值
u_1=zeros(3,1);u_2=u_1;u_3=u_2;   %控制率
h1i=zeros(3,1);h1i_1=h1i;  %第一个控制量
h2i=zeros(3,1);h2i_1=h2i;  %第二个控制量
h3i=zeros(3,1);h3i_1=h3i;  %第三个空置量
x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;   %隐含层输出 

%权值初始化
k0=0.03;

%第一层权值
w11=k0*rand(3,2);
w12=k0*rand(3,2);
w13=k0*rand(3,2);
%第二层权值
w21=k0*rand(1,9);
w22=k0*rand(1,9);
w23=k0*rand(1,9);

%值限定
ynmax=1;ynmin=-1;  %系统输出值限定
xpmax=1;xpmin=-1;  %P节点输出限定
qimax=1;qimin=-1;  %I节点输出限定
qdmax=1;qdmin=-1;  %D节点输出限定
uhmax=1;uhmin=-1;  %输出结果限定

%% 网络迭代优化
for k=1:1:200

    %% 控制量输出计算
    %--------------------------------网络前向计算--------------------------
    
    %系统输出
    y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);
    y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);
    y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);
    
    r1(k)=0.7;r2(k)=0.4;r3(k)=0.6;  %控制目标
    
    %系统输出限制
    yn=[y1(k),y2(k),y3(k)];
    yn(find(yn>ynmax))=ynmax;
    yn(find(ynxpmax))=xpmax;
    xp(find(xpqimax))=qimax;
    qi(find(qiqdmax))=qdmax;
    qd(find(qduhmax))=uhmax;
    uh(find(uh

4结果分析

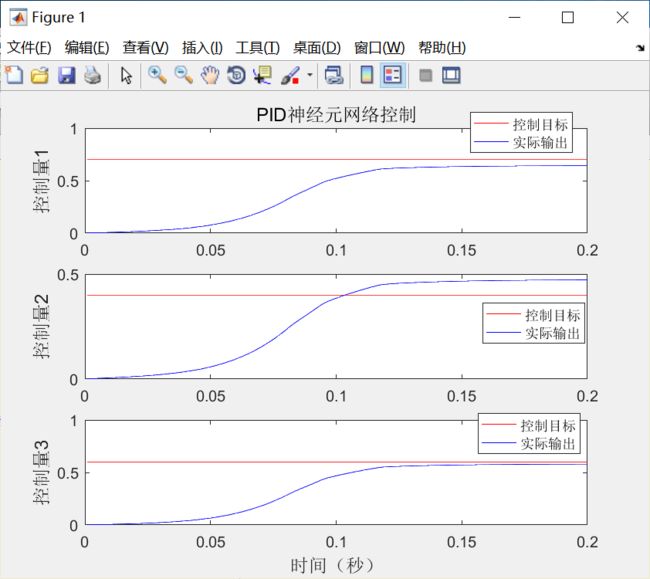
        用PID神经元网络控制式(6-10)中3输人3输出的复杂耦合系统,网络初始权值随机得到,网络权值学习率为0.05,控制间隔为0.001s,控制量的控制目标分别为0.7,0.4和0.6，PID神经元网络控制效果如图6-4所示。控制器控制误差如图6-5所示。

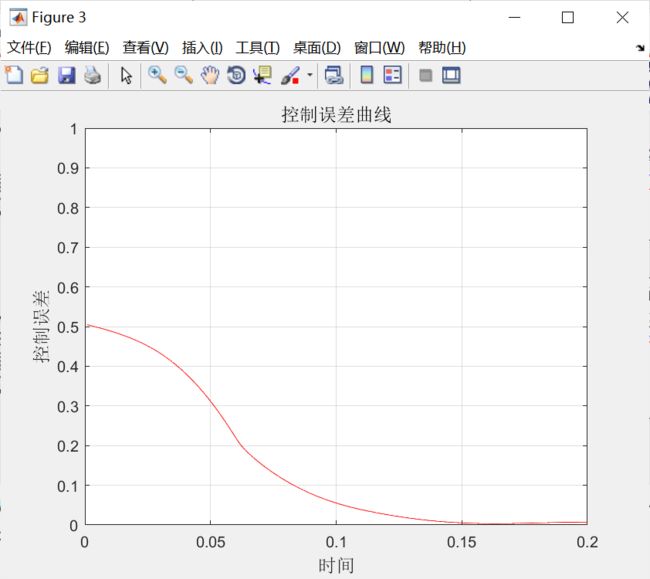
        从图6-4、图6-5可以看出,PID神经元控制器能够较好控制此多输人多输出复杂耦合系统,控制量最终值接近目标值。

5案例扩展

5.1 增加动量项

        PID神经元网络权值采用梯度学习算法,网络权值修正较慢并且容易陷入局部最优,可以通过增加动量项的方法提高网络学习效率 增加动量项的权值学习公式如下：
        带动量项的PID神经元网络控制效果如图所示。

5.2神经元系数

        PID神经网络控制器中隐含层三个节点分别对应着比例控制、积分控制和微分控制的三个环节。积分控制神经元的值在不断累加,造成积分神经元值不断累积增加,微分控制神经元的值为控制量当前值和目标值的差,微分控制神经元值过小。因此,借鉴PID控制器中PID参数设置,增加神经元输出乘积系数﹐隐含层输出值由隐含层神经元输出值乘以对应系数得到,计算公式如下:
5.3PID 神经元网络权值优化

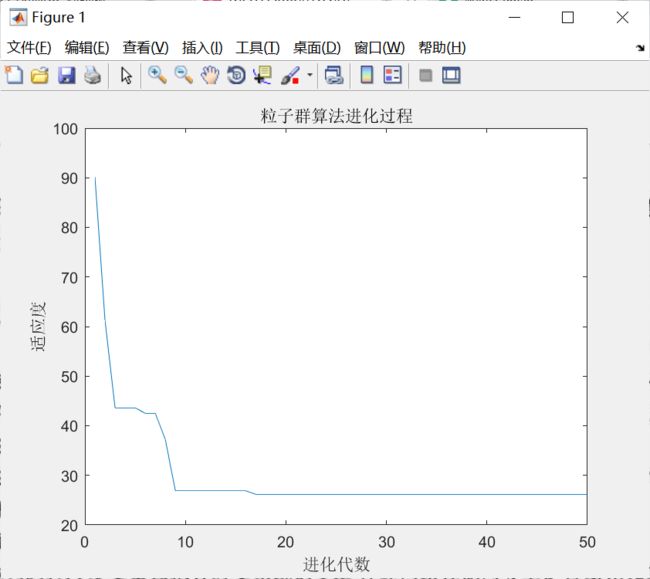
        PID神经元网络采用的学习算法是梯度学习法,初始权值随机得到,权值在学习过程中可能陷入局部最优值。采用粒子群算法优化神经元网络初始权值,粒子群算法的参数设置为:种群规模为50,进化次数40,采用自适应变异方法提高种群搜索能力,粒子群算法进化过程如图6-8所示。