【NCC】之四:计算协方差的提前退出条件
文章目录
-
- 1. 分析
- 2. Cauchy-Schwarz不等式
-
- Cauchy-Schwarz不等式:
- 3.应用
-
- 好了,万事大吉了吗?
- 一点改进
- 内层循环注意优化
- 再来一点改进
- 结果示例
1. 分析
在从Pearson相关系数到模板匹配的NCC方法这篇文章里面已经实现了一个暴力计算协方差的方法。暴力计算的方法不是没有用,在用FFT加速NCC的过程中你会发现采用FFT的方法可以计算全图的结果,但是差不多也到头了,没法用金字塔做加速。原因分析如下:
假设搜索图的尺寸为 M x × M y M_x\times M_y Mx×My,模板图的尺寸为 N x × N y N_x \times N_y Nx×Ny,计算两个图的协方差时可以转为卷积,不知道的请看here,直接计算和FFT加速NCC的计算复杂度如下图:
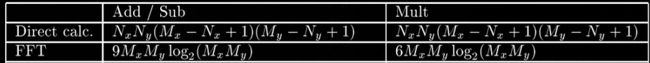
当我们能在金字塔顶层找到模板的粗略位置后,我们可以往下层回溯,只需要一个很小的搜索空间就可以,比如在下层中只要对应位置的 3 ∗ 3 3 * 3 3∗3或者 5 ∗ 5 5* 5 5∗5区域的搜索空间。按照上面的计算复杂度来看,写个这样简单的小函数可以帮我们分析一下复杂度

当金字塔向下回溯的区域采用3*3领域时,FFT计算量是直接计算的计算量的倍数表
| 尺寸 | add/sub | mul |
|---|---|---|
| 10 | 7.04 | 4.69 |
| 50 | 7.2 | 4.8 |
| 100 | 7.9 | 5.3 |
| 200 | 8.88 | 5.9 |
| 500 | 10.2 | 6.8 |
可以看到在搜索区域很小的时候用FFT在加法和乘法上的计算量都是直接计算的好多倍。所以直接计算卷积还是有存在的必要的。
2. Cauchy-Schwarz不等式
计算协方差
c o v ( S x , y , T ) = E ( S x , y T ) − E ( S x , y ) E ( T ) = Σ i = 1 m Σ j = 1 n S x , y ( i , j ) T ( i , j ) m n − S x , y ˉ T ˉ \begin{aligned} cov(S_{x,y},T) &=E(S_{x,y}T)-E(S_{x,y})E(T)\\ &=\frac{\Sigma_{i=1}^{m}\Sigma_{j=1}^{n}S_{x,y}(i,j)T(i,j)}{mn} - \bar{S_{x,y}}\bar{T} \end{aligned} cov(Sx,y,T)=E(Sx,yT)−E(Sx,y)E(T)=mnΣi=1mΣj=1nSx,y(i,j)T(i,j)−Sx,yˉTˉ
的时候我们会一直在计算
Σ i = 1 m Σ j = 1 n S x , y ( i , j ) T ( i , j ) \Sigma_{i=1}^{m}\Sigma_{j=1}^{n}S_{x,y}(i,j)T(i,j) Σi=1mΣj=1nSx,y(i,j)T(i,j)
这个式子也是NCC中最耗时的地方。
Cauchy-Schwarz不等式:
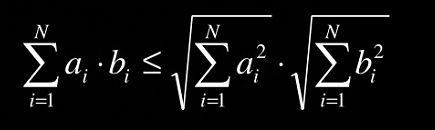
a i , b i ∈ R a_i,b_i \in R ai,bi∈R.
这个等式很好证明,设向量 a ⃗ = ( a 1 , a 2 , . . . , a N ) , b ⃗ = ( b 1 , b 2 , . . . , b N ) \vec{a}=(a_1,a_2,...,a_N),\vec{b}=(b_1,b_2,...,b_N) a=(a1,a2,...,aN),b=(b1,b2,...,bN). a ⃗ ⋅ b ⃗ = ∣ ∣ a ⃗ ∣ ∣ ⋅ ∣ ∣ b ⃗ ∣ ∣ ⋅ cos θ ≤ ∣ ∣ a ⃗ ∣ ∣ ⋅ ∣ ∣ b ⃗ ∣ ∣ \vec{a} \cdot \vec{b}=||\vec{a}|| \cdot ||\vec{b}|| \cdot \cos\theta \le ||\vec{a}|| \cdot ||\vec{b}|| a⋅b=∣∣a∣∣⋅∣∣b∣∣⋅cosθ≤∣∣a∣∣⋅∣∣b∣∣,到这里相信读过高中的都知道了。
3.应用
利用不等式我们是想在某些情况下可以直接跳出这一个侯选位置的计算,按照NCC的计算规则如果我们把计算协方差的部分放大到右侧,那我们就可以得到当前图像的NCC值的上界,而这个上界我们可以用平方积分图在 O ( 1 ) O(1) O(1)的复杂度内计算出来。如果上界的NCC值比当前最好的NCC还小,那我们不是就可以不去计算协方差了!!!非常好的想法!
但是上面的不等式还不能直接用,因为如果你直接用的话你就会发现这个上界有时候有点太大了,根本没法达到过滤一些不好的候选点的作用。需要放小一点。
把上界改成下面这样:
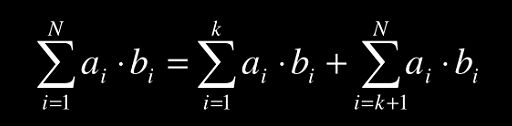
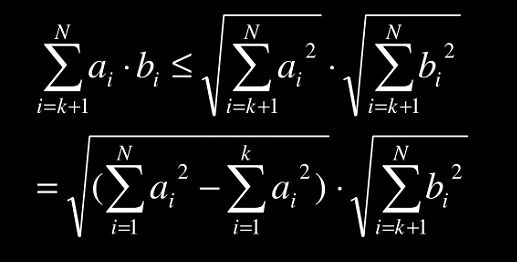
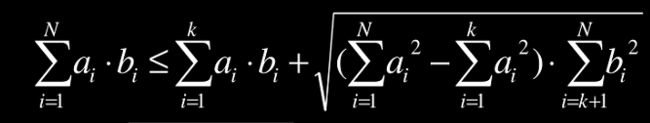
前面一部分用真实值,只放大后面一部分,这样的话随着 ∑ a i b i \sum a_ib_i ∑aibi的增加这个上界值越来越小,也越来越接近真实的NCC值。当上界小于当前最大NCC时推出此次候选图的匹配计算。
在上面的式子中,我们需要累加两个值 ∑ i = 1 k a i b i , ∑ i = 1 k a i 2 \sum_{i=1}^{k} a_ib_i,\sum_{i=1}^{k}a_i^2 ∑i=1kaibi,∑i=1kai2,而 ∑ i = k + 1 N b i 2 \sum_{i=k+1}^{N}b_i^2 ∑i=k+1Nbi2是模板的信息可以离线计算出来形成一个查找表,直接索引就行(最好把根号也带着计算进去,能离线做的都离线做,开方运算相对来说是很慢的)。
好了,万事大吉了吗?
当我呼哧呼哧写完如下代码,暴力匹配的结果opencv比我的快302倍,变为了快425倍!也就是说反而变慢了。
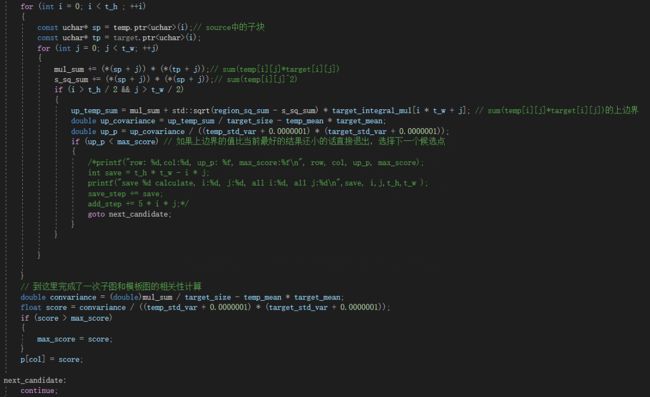
temp是候选的子图,target是模板图。上面的动作就是来计算 ∑ a i b i \sum a_ib_i ∑aibi的。
我把跳出循环的位置打印出来看,发现大多数都会到遍历到图像的1/3 or 1/2左右退出循环,但是在这个最内层循环里面我们加了很多计算,多了十几次加法,几次乘法,还有一次判断,一次开方运算。在最原始的计算里面我们只要mul_sum += a_i*b_i这一句就行了,现在多了这么多计算量,虽说是提前跳出循环了,但是弥补不了增加的。
一点改进
为了不增加太多的多余的计算,我们改为从图像的中心点(th/2,tw/2)以后才开始计算上界。
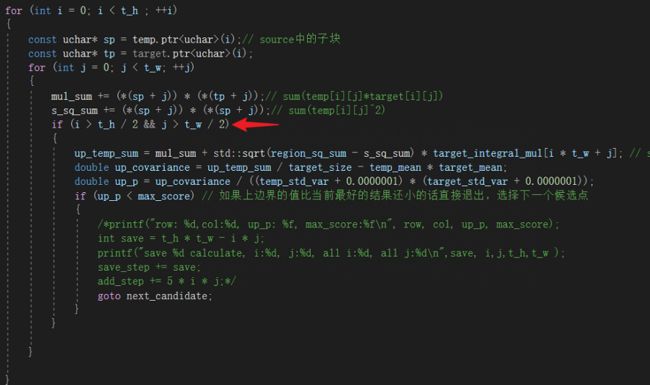
此时opencv的速度比我的从快425倍降为了148倍,比直接暴力计算的快了一些。
内层循环注意优化
最内层的判断条件了吗,带着2次除法,但是这个量是可以提前计算的,把它提前计算出来。opencv的速度从我的148倍变为128倍,这点小改动还是有效果,因为在最内层循环里面,可能减少一次计算整个程序就减少几万次的计算了,比如一个100*100的模板图在内层就相当于减少了20000次除法,再乘上上面外层的循环,那就是非常可观的了。
另外在条件判断中i>th/2 应该在 j>tw/2前面,因为在上半图中i一直小于th/2,不会到后面一个条件的判断,如果把后一项提前,那在子图的右上部分遍历的时候都会多一次条件判断。因为编译器优化的&&操作只要前面一个条件不满足就直接跳过了。
再来一点改进
我们现在是计算NCC的上限值,其实可以计算一个中间结果,这个中间结果如果小于当前最优的NCC值对应的中间结果,那也就可以直接退出了,并不需要把NCC的上限值真的算出来。但是不能想当然的直接记录up_temp_sum作为中间结果,因为NCC的计算中还有一个方差和均值。
结果示例
以下的结果是我没有加条件判断(i>th/2 && j>w/2)的时候得到的,并且为了显示我把next_candidate放到计算NCC的前面了,在正常运行中跳出循环了的话这些值是没必要计算的。
下面左侧为搜索图,中间为模板图,右侧为NCC结果的map图。可以看到在得到最大的NCC值后,后面的NCC值都很小,因为很早就跳出来了。

正常情况下这个结果图长下面这样,有跳出循环的地方都不会计算NCC值了,从图上也可以看到,可能超过99%的侯选位置都会因为不满足条件而退出循环。
