数据结构day8（2023.7.25）

一、排序算法

排序：把无需序列转换为有序序列的一种算法。

内排：在计算机内存中实现的排序算法【多用适用于数据量较小的情况】

外排：在计算机内存以及外部介质实现的排序算法【先内存，在外部】

排序的分类：

交换排序：冒泡排序、快速排序

插入排序：直接插入排序，希尔排序

选择排序：简单选择排序、堆排序

归并排序：二路归并【内+外】、多路归并【外】

基数排序

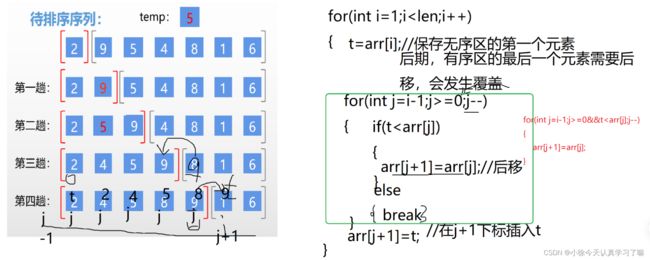
1.1 直接插入排序

       插入排序是指在待排序的元素中，假设前面n-1(其中n>=2)个数已经是排好顺序的，现将第n个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。 时间复杂度：O(n^2) 稳定

代码见前面day6的CSDN 

1.2 快速排序

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

(1)首先设定一个分界值，通过该分界值将数组分成左右两部分。 

(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于分界值，而右边部分中各元素都大于或等于分界值。 

(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。 

(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

#include 
#include 
#include 
/*
 * function:    一轮排序
 * @param [ in] 
 * @param [out] 
 * @return      返回基准值的下表
 */
int one_sort(int arr[],int low,int high)
{
    int key=arr[low];//确定数组的第一个元素为基准值
    //low==high  循环结束
//    1  34  45   23  56
//    l
//h
    while(low=arr[low])
        {
            low++;
        }
        arr[high]=arr[low];
    }
arr[low]=key;//把基准值插入到数组中  low/high就是基准值的下表
    return low;//high

}
void quick_sort(int arr[],int low,int high)
{
    //没有元素low>high
    //只有一个元素：low==high
    if(low>=high)
        return;
    
    //一轮排序
    int mid=one_sort(arr,low,high);
    //递归左边：递归左子树
    
    quick_sort(arr,low,mid-1);
    //递归右边：递归右子树
    quick_sort(arr,mid+1,high);
}
int main(int argc, const char *argv[])
{
    int arr[]={12,3,34,23,14,45,76,23,12};
    int len=sizeof(arr)/sizeof(arr[0]);
    quick_sort(arr,0,len-1);

    for(int i=0;i

1.3 冒泡排序

冒泡排序算法的原理如下：

①比较相邻的元素。如果第一个比第二个大，就交换他们两个。

②对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。 

③针对所有的元素重复以上的步骤，除了最后一个。

④持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

for(int i=1;iarr[j+1])    
        {
            t=arr[j];arr[j]=arr[j+1];arr[j+1]=t;        
        }
    }
}

1.4 简单选择排序

简单选择排序算法原理：每次从左至右扫描序列，记下最小值的位置。

for(int i=0;i arr[j])
        {
            min=j;        
        }
    }
    if(min!=i)
    {
        t=arr[min];arr[min]=arr[i];arr[i]=t;    
    }
}

1.5 总结

排序名	类型	时间复杂度	稳定性
冒泡排序	交换排序	O(n^2)	稳定
快速排序	交换排序	O(nlog2n)	不稳定
简单选择排序	选择排序	O(n^2)	不稳定
直接插入排序	插入排序	O(n^2)	稳定
希尔排序	插入排序	O(n^1.5)	不稳定
二路归并	归并排序	O(nlog2n)	稳定