8.4 利用集成运放实现的信号转换电路
在控制、遥控、遥测、近代生物物理和医学等领域,常常需要将模拟信号进行转换,如将信号电压转换成电流,将信号电流转换成电压,将直流信号转换成交流信号,将模拟信号转换成数字信号,等等。
一、电压 - 电流转换电路
在控制系统中,为了驱动执行机构,如记录仪、继电器等,常需要将电压转换成电流;而在监测系统中,为了数字化显示,又常将电流转换成电压,再接数字电压表。在放大电路中引入合适的反馈,就可实现上述转换。
1、电压 - 电流转换电路

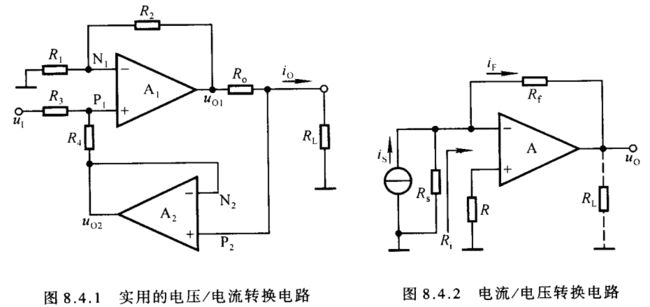
如图6.7.1所示为电压 - 电流转换电路,图(a)所示为基本原理电路,图(b)所示为负载接地的豪兰德电流源电路。图8.4.1所示电路为另一种负载接地的实用电压 - 电流转换电路。 A 1 A_1 A1、 A 2 A_2 A2 均引入了负反馈,前者构成同相求和运算电路,后者构成电压跟随器。图中 R 1 = R 2 = R 3 = R 4 = R R_1=R_2=R_3=R_4=R R1=R2=R3=R4=R,因此 u O 2 = u P 2 u_{\scriptscriptstyle O2}=u_{\scriptscriptstyle P2} uO2=uP2 u P 1 = R 4 R 3 + R 4 ⋅ u I + R 3 R 3 + R 4 ⋅ u P 2 = 0.5 u I + 0.5 u P 2 ( 8.4.1 ) u_{\scriptscriptstyle P1}=\frac{R_4}{R_3+R_4}\cdot u_{\scriptscriptstyle I}+\frac{R_3}{R_3+R_4}\cdot u_{\scriptscriptstyle P2}=0.5u_{\scriptscriptstyle I}+0.5u_{\scriptscriptstyle P2}\kern 10pt(8.4.1) uP1=R3+R4R4⋅uI+R3+R4R3⋅uP2=0.5uI+0.5uP2(8.4.1) u O 1 = ( 1 + R 2 R 1 ) u P 1 = 2 u P 1 u_{\scriptscriptstyle O1}=(1+\frac{R_2}{R_1})u_{\scriptscriptstyle P1}=2u_{\scriptscriptstyle P1} uO1=(1+R1R2)uP1=2uP1将式(8.4.1)代入上式, u O 1 = u P 2 + u I u_{\scriptscriptstyle O1}=u_{\scriptscriptstyle P2}+u_{\scriptscriptstyle I} uO1=uP2+uI, R o R_o Ro 上的电压 u R o = u O 1 − u P 2 = u I u_{\scriptscriptstyle R_o}=u_{\scriptscriptstyle O1}-u_{\scriptscriptstyle P2}=u_{\scriptscriptstyle I} uRo=uO1−uP2=uI所以 i O = u I R o ( 8.4.2 ) i_{\scriptscriptstyle O}=\frac{u_{\scriptscriptstyle I}}{R_o}\kern 40pt(8.4.2) iO=RouI(8.4.2)与豪兰德电流源电路的表达式[式(6.7.4)]相比,仅差符号。
2、电流 - 电压转换电路
集成运放引入电压并联负反馈即可实现电流 - 电压转换,如图8.4.2所示,在理想运放条件下,输入电阻 R i f = 0 R_{if}=0 Rif=0,因而 i F = i S i_{\scriptscriptstyle F}=i_{\scriptscriptstyle S} iF=iS,故输出电压 u O = − i S R f ( 8.4.3 ) u_{\scriptscriptstyle O}=-i_{\scriptscriptstyle S}R_f\kern 40pt(8.4.3) uO=−iSRf(8.4.3)应当指出,因为实际电路的 R i f R_{if} Rif 不可能为零,所以 R s R_{s} Rs 比 R i f R_{if} Rif 大得愈多,转换精度愈高。
二、精密整流电路
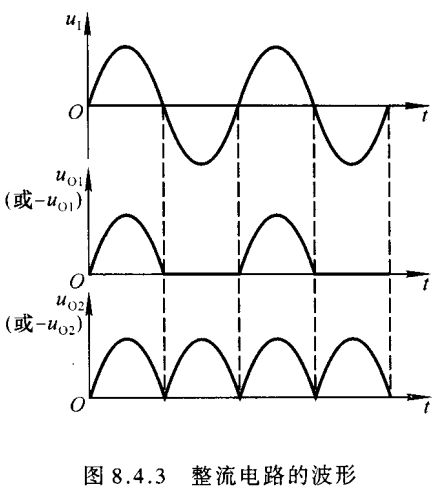
将交流电转换为直流电,称为整流。精密整流电路的功能是将微弱的交流电压转换成直流电压。整流电路的输出保留输入电压的形状,而仅仅改变输入电压的相位。当输入电压为正弦波时,半波整流电路和全波整流电路的输出电压波形如图8.4.3中 u O 1 u_{\scriptscriptstyle O1} uO1 和 u O 2 u_{\scriptscriptstyle O2} uO2 所示。
在图8.4.4(a)所示的一般半波整流电路中,由于二极管的伏安特性如图(b)所示,当输入电压 u I u_{\scriptscriptstyle I} uI 幅值小于二极管的开启电压 U O N U_{ON} UON 时,二极管在信号的整个周期均处于截止状态,输出电压始终为零。即使 u I u_{\scriptscriptstyle I} uI 幅值足够大,输出电压也只反映 u I u_{\scriptscriptstyle I} uI 大于 U O N U_{ON} UON 的那部分电压的大小。因此,该电路不能对微弱信号整流。
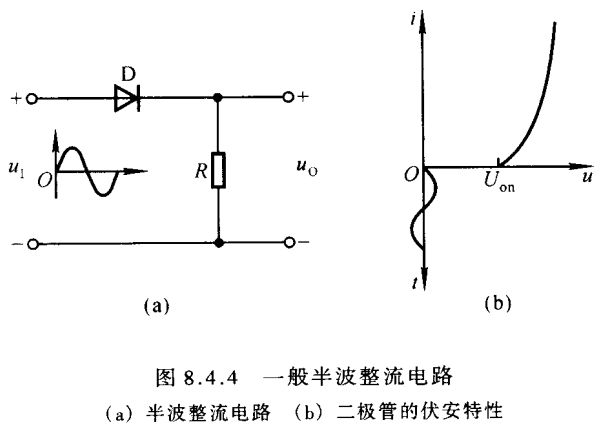
图8.4.5(a)所示为半波精密整流电路。当 u I > 0 u_{\scriptscriptstyle I}>0 uI>0 时,必然使集成运放的输出 u O ′ < 0 u'_{\scriptscriptstyle O}<0 uO′<0,从而导致二极管 D 2 D_2 D2 导通, D 1 D_1 D1 截止,电路实现反相比例运算,输出电压 u O = − R f R ⋅ u I ( 8.4.5 ) u_{\scriptscriptstyle O}=-\frac{R_f}{R}\cdot u_{\scriptscriptstyle I}\kern 30pt(8.4.5) uO=−RRf⋅uI(8.4.5)当 u I < 0 u_{\scriptscriptstyle I}<0 uI<0 时,必然使集成运放的输出 u O ′ > 0 u'_{\scriptscriptstyle O}>0 uO′>0,从而导致二极管 D 1 D_1 D1 导通, D 2 D_2 D2 截止, R f R_f Rf 中电流为零,因此输出电压 u O = 0 u_{\scriptscriptstyle O}=0 uO=0。 u I u_{\scriptscriptstyle I} uI 和 u O u_{\scriptscriptstyle O} uO 的波形如图(b)所示。
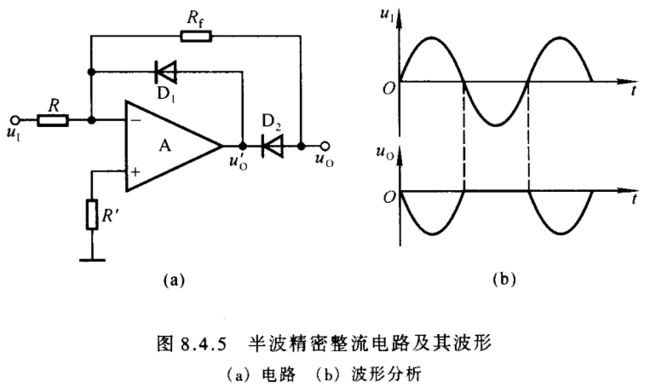
如果设二极管的导通电压为 0.7 V 0.7\,\textrm V 0.7V,集成运放的开环差模放大倍数为 50 50 50 万倍,那么为使二极管 D 1 D_1 D1 导通,集成运放的净输入电压 u P − u N = ( 0.7 5 × 1 0 5 ) V = 0.14 × 1 0 − 5 V = 1.4 μV u_{\scriptscriptstyle P}-u_{\scriptscriptstyle N}=(\frac{0.7}{5\times10^5})\,\textrm V=0.14\times10^{-5}\,\textrm V=1.4\,\textrm{μV} uP−uN=(5×1050.7)V=0.14×10−5V=1.4μV同理可估算出为使 D 2 D_2 D2 导通集成运放所需的净输入电压,也是同数量级。可见,只要输入电压 u I u_{\scriptscriptstyle I} uI 使集成运放的净输入电压产生非常微小的变化,就可以改变 D 1 D_1 D1 和 D 2 D_2 D2 的工作状态,从而达到精密整流的目的。
图8.4.5(b) 所示波形说明当 u I > 0 u_{\scriptscriptstyle I}>0 uI>0 时 u O = − K u I ( K > 0 ) u_{\scriptscriptstyle O}=-Ku_{\scriptscriptstyle I}(K>0) uO=−KuI(K>0),当 u I < 0 u_{\scriptscriptstyle I}<0 uI<0 时, u O = 0 u_{\scriptscriptstyle O}=0 uO=0。那么,若利用反相求和电路将 − K u I -Ku_{\scriptscriptstyle I} −KuI 与 u I u_{\scriptscriptstyle I} uI 负半周波形相加,就可实现全波整流,电路如图8.4.6(a)所示。
分析由 A 2 A_2 A2 所组成的反相求和运算电路可知,输出电压 u O = − u O 1 − u I u_{\scriptscriptstyle O}=-u_{\scriptscriptstyle O1}-u_{\scriptscriptstyle I} uO=−uO1−uI当 u I > 0 u_{I}>0 uI>0 时, u O 1 = − 2 u I u_{\scriptscriptstyle O1}=-2u_{\scriptscriptstyle I} uO1=−2uI, u O = 2 u I − u I = u I u_{\scriptscriptstyle O}=2u_{\scriptscriptstyle I}-u_{\scriptscriptstyle I}=u_{\scriptscriptstyle I} uO=2uI−uI=uI;当 u I < 0 u_{\scriptscriptstyle I}<0 uI<0 时, u O 1 = 0 u_{\scriptscriptstyle O1}=0 uO1=0, u O = − u I u_{\scriptscriptstyle O}=-u_{\scriptscriptstyle I} uO=−uI;所以 u O = ∣ u I ∣ ( 8.4.5 ) u_{\scriptscriptstyle O}=|u_{\scriptscriptstyle I}|\kern 40pt(8.4.5) uO=∣uI∣(8.4.5)故图8.4.6(a)所示电路也称为绝对值电路。当输入电压为正弦波和三角波时,电路输出波形分别如图(b)和(c)所示。

【例8.4.1】分析图8.4.7所示电路输出电压与输入电压间的关系,并说明电路功能。已知 R 1 = R 2 R_1=R_2 R1=R2。
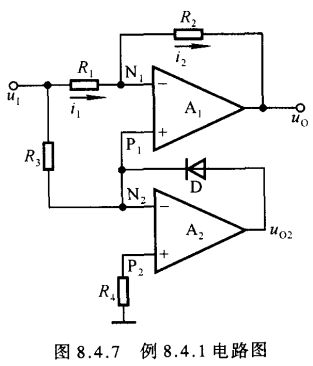
解: 当 u I > 0 u_{\scriptscriptstyle I}>0 uI>0 时, u O 2 < 0 u_{\scriptscriptstyle O2}<0 uO2<0,二极管 D D D 截止,故 u P 1 = u N 2 = u I u_{\scriptscriptstyle P1}=u_{\scriptscriptstyle N2}=u_{\scriptscriptstyle I} uP1=uN2=uI,使 i 1 = i 2 = 0 i_1=i_2=0 i1=i2=0,因而 u O = u I u_{\scriptscriptstyle O}=u_{\scriptscriptstyle I} uO=uI。
当 u I < 0 u_{\scriptscriptstyle I}<0 uI<0 时, u O 2 > 0 u_{\scriptscriptstyle O2}>0 uO2>0, D D D 导通, u P 1 = u N 2 = u P 2 = 0 u_{\scriptscriptstyle P1}=u_{\scriptscriptstyle N2}=u_{\scriptscriptstyle P2}=0 uP1=uN2=uP2=0,为虚地,故 u O = − R 2 R 1 ⋅ u I = − u I u_{\scriptscriptstyle O}=-\frac{R_2}{R_1}\cdot u_{\scriptscriptstyle I}=-u_{\scriptscriptstyle I} uO=−R1R2⋅uI=−uI因此 u O = ∣ u I ∣ u_{\scriptscriptstyle O}=|u_{\scriptscriptstyle I}| uO=∣uI∣电路的功能是实现精密全波整流,或者说构成绝对值电路。
通过精密整流电路的分析可知,当分析含有二极管(或三极管、场效应管)的电路时,一般应首先判断管子的工作状态,然后求解输出与输入信号间的函数关系。而管子的工作状态通常决定于输入电压(如整流电路)或输出电压(如压控振荡电路)的极性。
三、电压 - 频率转换电路
电压 - 频率转换电路(VFC:Voltage Frequency Converter)的功能是将输入直流电压转换成频率与其数值成正比的输出电压,故也称为电压控制振荡电路(VCO:Voltage Controlled Oscillator),简称压控振荡电路。通常,它的输出是矩形波。任何物理量通过传感器转换成电信号后,经预处理变换为合适的电压信号,然后去控制压控振荡电路,再用压控振荡电路的输出驱动计数器,使之在一定时间间隔内记录矩形波个数,并用数码显示,那么就可以得到该物理量的数字式测试仪表,如图8.4.8所示。因此,可以认为电压 - 频率转换电路是一种模拟量到数字量的转换电路,即模/数转换电路。电压 - 频率转换电路广泛应用于模拟/数字信号的转换、调频、遥控遥测等各种设备之中。
1、由集成运放构成的电压 - 频率转换电路
(1)电荷平衡式电路
电荷平衡式电压 - 频率转换电路由积分器和滞回比较器组成,它的一般原理框图如图8.4.9所示。图中 S \textrm S S 为电子开关,受输出电压 u O u_{\scriptscriptstyle O} uO 的控制。
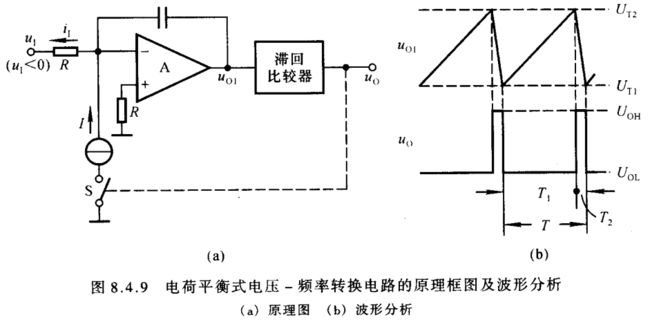
设 u I < 0 u_{\scriptscriptstyle I}<0 uI<0, ∣ I ∣ > > ∣ i I ∣ |I|>>|i_{\scriptscriptstyle I}| ∣I∣>>∣iI∣; u O u_{\scriptscriptstyle O} uO 的高电平为 U O H U_{OH} UOH, u O u_{\scriptscriptstyle O} uO 的低电平为 U O L U_{OL} UOL;当 u O = U O H u_{\scriptscriptstyle O}=U_{OH} uO=UOH 时 S \textrm S S 闭合,当 u O = U O L u_{\scriptscriptstyle O}=U_{OL} uO=UOL 时 S \textrm S S 断开。若初态 u O = U O L u_{\scriptscriptstyle O}=U_{OL} uO=UOL, S \textrm S S 断开,积分器对输入电流 i I i_{\scriptscriptstyle I} iI 积分,且 i I = u I / R i_{\scriptscriptstyle I}=u_{\scriptscriptstyle I}/R iI=uI/R, u O 1 u_{\scriptscriptstyle O1} uO1 随时间逐渐上升;当增大到一定数值时, u O u_{\scriptscriptstyle O} uO 从 U O L U_{OL} UOL 跃变为 U O H U_{OH} UOH,使 S \textrm S S 闭合,积分器对恒流源电流 I I I 与 i I i_{\scriptscriptstyle I} iI 的差值积分,且 I I I 与 i I i_{\scriptscriptstyle I} iI 的差值近似为 I I I, u O 1 u_{\scriptscriptstyle O1} uO1 随时间下降;因为 ∣ I ∣ > > ∣ i I ∣ |I|>>|i_{\scriptscriptstyle I}| ∣I∣>>∣iI∣,所以 u O 1 u_{\scriptscriptstyle O1} uO1 下降速度远大于其上升速度;当 u O 1 u_{\scriptscriptstyle O1} uO1 减小到一定数值时, u O u_{\scriptscriptstyle O} uO 从 U O H U_{OH} UOH 跃变为 U O L U_{OL} UOL,回到初态,电路重复上述过程,产生自激振荡,波形如图(b)所示。由于 T 1 > > T 2 T_1>>T_2 T1>>T2,可以认为振荡周期 T ≈ T 1 T\approx T_1 T≈T1。而且, u I u_{\scriptscriptstyle I} uI 的数值愈大, T 1 T_1 T1 愈小,振荡频率 f f f 愈高,因此实现了电压 - 频率转换,或者说实现了压控振荡。由于电流源 I I I 对电容 C C C 在很短时间内放电(或称反向充电)的电荷量等于 i I i_{\scriptscriptstyle I} iI 在较长时间内充电(或称正向充电)的电荷量,故称这类电路为电荷平衡式电路。
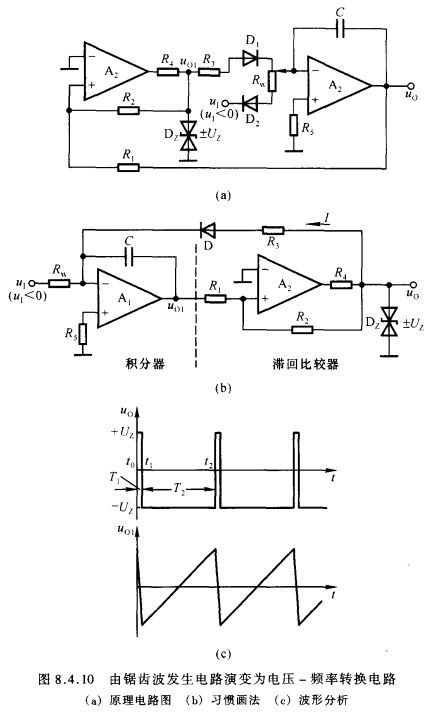
图8.3.10(a)所示锯齿波发生电路中,若将电位器滑动端置于最上端,且积分电路正向积分决定于输入电压,则构成压控振荡电路,如图8.4.10(a)所示,这是电荷平衡式电压 - 频率转换电路的一种。在实际电路中,将图(a)中的 D 2 D_2 D2 省略,将 R w R_w Rw 换为固定电阻,并习惯画成为图(b)所示电路,两个集成运放输出电压的波形如图(c)所示。对锯齿波发生电路进行定量分析可得,图(b)所示电路中滞回比较器的阈值电压为 ± U T = ± R 1 R 2 ⋅ U Z ±U_T=±\frac{R_1}{R_2}\cdot U_Z ±UT=±R2R1⋅UZ在图(c)波形中的 T 2 T_2 T2 时间段, u O 1 u_{\scriptscriptstyle O1} uO1 是对 u I u_{\scriptscriptstyle I} uI 的线性积分,其起始值为 − U T -U_T −UT,终了值为 + U T +U_{T} +UT,因而 T 2 T_2 T2 应满足 U T = − 1 R w C ⋅ u I T 2 − U T U_T=-\frac{1}{R_wC}\cdot u_{\scriptscriptstyle I}T_2-U_T UT=−RwC1⋅uIT2−UT解得 T 2 = 2 R 1 R w C R 2 ⋅ U Z ∣ u I ∣ T_2=\frac{2R_1R_wC}{R_2}\cdot\frac{U_Z}{|u_{\scriptscriptstyle I}|} T2=R22R1RwC⋅∣uI∣UZ当 R w > > R 3 R_w>>R_3 Rw>>R3 时,振荡周期 T ≈ T 2 T\approx T_2 T≈T2,故振荡频率 f ≈ 1 T 2 = R 2 2 R 1 R w C U Z ⋅ ∣ u I ∣ ( 8.4.6 ) f\approx\frac{1}{T_2}=\frac{R_2}{2R_1R_wCU_Z}\cdot|u_{\scriptscriptstyle I}|\kern 20pt(8.4.6) f≈T21=2R1RwCUZR2⋅∣uI∣(8.4.6)振荡频率受控于输入电压。
(2)复位式电路
复位式电压 - 频率转换电路的原理框图如图8.4.11所示,电路由积分器和单限比较器组成, S \textrm S S 为模拟电子开关,可由晶体管或场效应管组成。设输出电压 u O u_{\scriptscriptstyle O} uO 为高电平 U O H U_{OH} UOH 时 S \textrm S S 断开, u O u_{\scriptscriptstyle O} uO 为低电平 U O L U_{OL} UOL 时 S \textrm S S 闭合。当电源接通后,由于电容 C C C 上电压为零,即 u O 1 = 0 u_{\scriptscriptstyle O1}=0 uO1=0,使 u O = U O H u_{\scriptscriptstyle O}=U_{OH} uO=UOH, S \textrm S S 断开,积分器对 u I u_{\scriptscriptstyle I} uI 积分, u O 1 u_{\scriptscriptstyle O1} uO1 逐渐减小;一旦 u O 1 u_{\scriptscriptstyle O1} uO1 过基准电压 − U R E F -U_{REF} −UREF, u O u_{\scriptscriptstyle O} uO 将从 U O H U_{OH} UOH 跃变为 U O L U_{OL} UOL,导致 S \textrm S S 闭合,使 C C C 迅速放电至零,即 u O 1 = 0 u_{\scriptscriptstyle O1}=0 uO1=0,从而 u O u_{\scriptscriptstyle O} uO 从 U O L U_{OL} UOL 跃变为 U O H U_{OH} UOH; S \textrm S S 又断开,重复上述过程,电路产生自激振荡,波形如图(b)所示。 u I u_{\scriptscriptstyle I} uI 愈大, u O 1 u_{\scriptscriptstyle O1} uO1 从零变化到 U R E F U_{REF} UREF 所需时间愈短,振荡频率也就愈高。
注: 由于使用的是单限电压比较器, u O 1 u_{\scriptscriptstyle O1} uO1 从 − U R E F -U_{REF} −UREF 到 0 的时间与 u O u_{\scriptscriptstyle O} uO 从低电平跳变到高电平的时间并不相同,但是它们的时间都比较短,所以可以认为其时间为 T 2 T_2 T2, T 2 < < T 1 T_2<
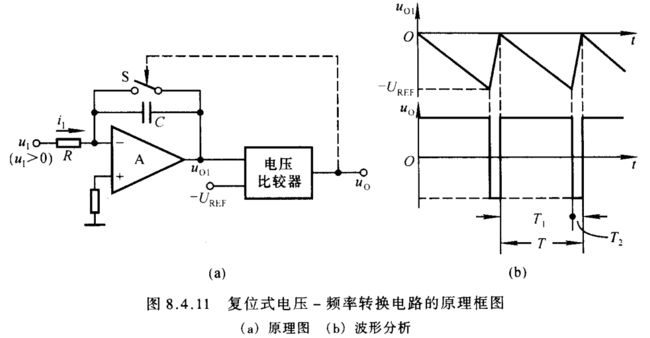
图8.4.12所示为复位式电压 - 频率转换电路,其振荡周期 T T T 和频率 f f f 为 T ≈ R 1 C ⋅ U R E F u I ( 8.4.7 ) T\approx R_1C\cdot\frac{U_{REF}}{u_{\scriptscriptstyle I}}\kern 30pt(8.4.7) T≈R1C⋅uIUREF(8.4.7) f ≈ u I R 1 C U R E F ( 8.4.8 ) f\approx\frac{u_{\scriptscriptstyle I}}{R_1CU_{REF}}\kern 30pt(8.4.8) f≈R1CUREFuI(8.4.8)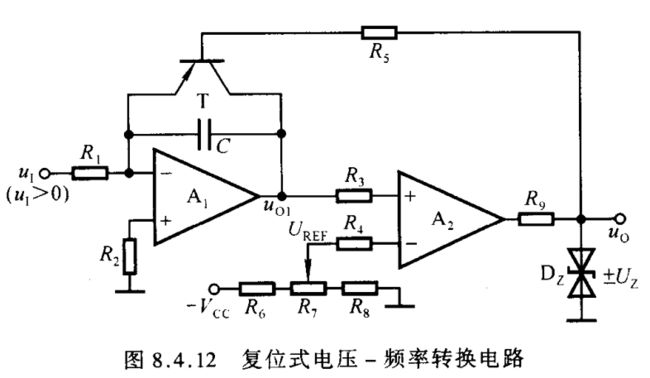
2、集成电压 - 频率转换电路
集成电压 - 频率转换电路分为电荷平衡式(如 AD650、VFC101)和多谐振荡器式(如 AD654)两类,它们的性能比较见表8.4.1。
表 8.4.1 集成电压 − 频率转换电路的主要性能指标 表8.4.1\,\, 集成电压 - 频率转换电路的主要性能指标 表8.4.1集成电压−频率转换电路的主要性能指标
| 指标参数 | 单位 | AD650 | AD654 |
|---|---|---|---|
| 满刻度频率 | MHz | 1 | 0.5 |
| 非线性 | % | 0.005 | 0.06 |
| 电压输入范围 | V | -10 ~ 0 | 0 ~ ( V S − 4 V_S-4 VS−4)(单电源供电) − V S \\-V_S −VS~( V S − 4 V_S-4 VS−4)(双电源供电) |
| 输入阻抗 | kΩ | 250 | 250 × 1 0 3 250×10^3 250×103 |
| 电源电压范围 | V | ±9 ~ ±18 | 单电源供电:4.5 ~ 3.6 \\\, 双电源供电:±5 ~ ±18 |
| 电源电流最大值 | mA | 8 | 3 |
表中参数表明,电荷平衡式电路的满刻度输出频率高,线性误差小,但其输入阻抗低,必须正、负双电源供电,且功耗大。多谐振荡器式电路功耗低,输入阻抗高,而且内部电路结构简单,输出为方波,价格便宜,但不如前者精度高。
很多集成电压 - 频率转换电路均可方便地实现频率 - 电压转换,如型号为 AD650 和 AD654 的集成电路。