【使用回溯法求解八皇后问题（92个解）】

在每一个横列、竖列、斜列都只有一个皇后
解决的冲突

包括行、列和两条对角线

规定每一行放置一个皇后，不会造成行上的冲突
当第col列被某个皇后占领之后，则同一列上的所有空格都不能再放置皇后，并且要把flag[col]置为被占领状态
对角线有两个方向，当第n行第col列皇后占领之后，要同时把以上下对角线标记置为被占领状态

---

程序的结构

初始化（清除棋盘）
循环八次
	1 放置一个皇后
	2 检查是否满足条件，如果满足，登记皇后的位置
	3 如果不满足，则退回，增加一步后再放置皇后
直到放到最后一个皇后

---

函数的定义

generate函数：找到n个皇后适合的位置
（找到第n-1个皇后合适的位置）、（找到第n个皇后合适的位置）
递归的终止条件是：找到最后一个皇后的位置

---

执行的过程

1、将数据进行初始化
2、从col列开始摆放第n个皇后（因为这样可以符合每一竖列一个皇后的要求），挨个去测试列是否可行，先测试当前位置（n，col）是否安全：
	如果是安全的，那么就去摆放第n个皇后，并且宣布占领（记得要横行竖列斜列一起来）
	如果没有测试完所有的行
		递归测试下一行generate（n+1）
		当n等于7（0-7）的时候，打印结果
	如果当n>=7时，发现此时已经无法摆放或者摆放完毕的时候，就要进行回溯了
3、输出结果

---

数据结构

place：int数组[0..7];
	第n行皇后所占据的列号
	主要用于输出结果
flag：bool数组[0..7];
	表示col列上是否可以放置皇后
d1：bool数组[0..14];
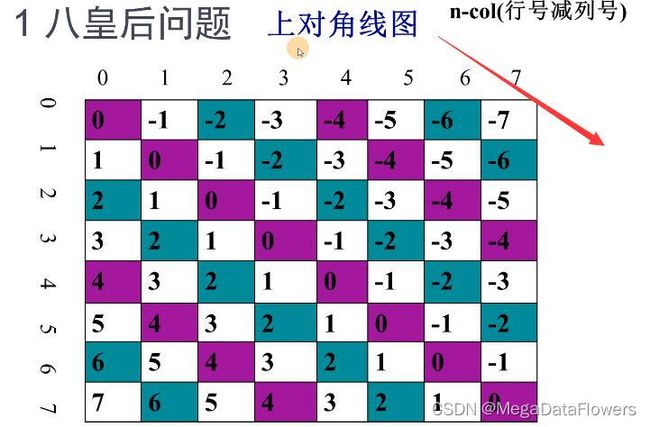
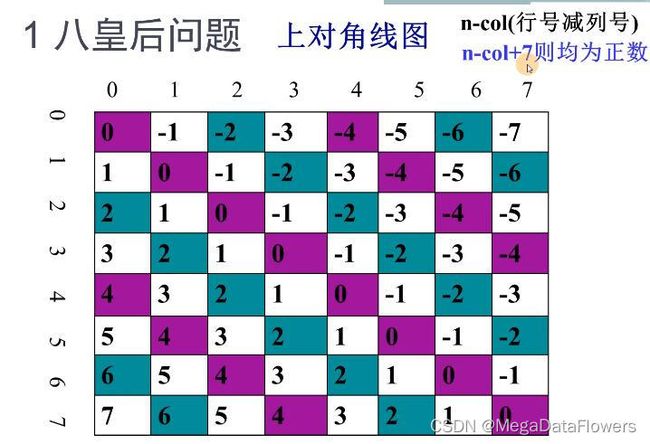
	(n,col)所在上对角线上是否可以放置皇后
d2：bool数组[0..14];
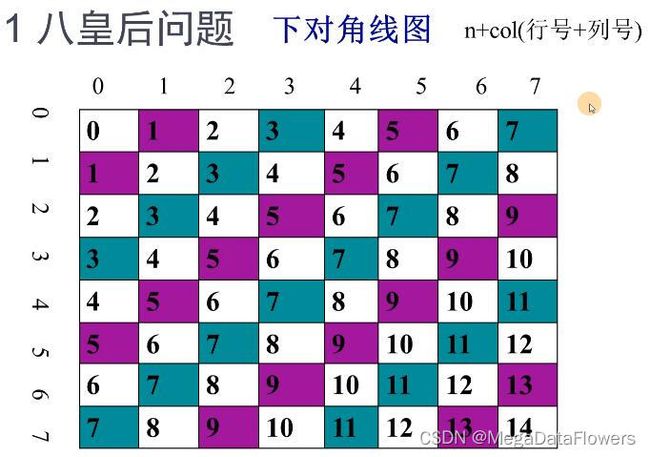
	(n,col)所在下对角线上是否可以放置皇后

---

上对角线

行号减去列号

处理上对角线

行号减去列号加上7来处理（处理为正数）

---

下对角线

行号加上列号

---

编程思路

1、是否可以放置皇后
2、放置皇后
3、删除皇后（回溯）

# include 
# include 

int place[8] = { 0 };	// 保存皇后的位置，下标为行，储存的数据为列。

bool flag[8] = { 1, 1, 1, 1, 1, 1, 1, 1 };	// 用来保存哪一列已经存在皇后 

bool d1[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };	
// 从左上到右下的对角线为上对角线，每条上对角线上的行和列的差是一样的。
bool d2[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };	
// 从左下到右下的对角线为下对角线，每条下对角线上的行和列的和是一样的。

int key = 0;					// 统计解的数量

// 函数声明
void QueenVIII(int);			// 八皇后问题
void output(void);				// 输出

// 主函数
int main(void)
{
	QueenVIII(0);
	return 1;
}

// 八皇后问题
void QueenVIII(int n)
{
	for (int i = 0; i < 8; ++i)	// 计算第n行皇后的位置
	{
		if (flag[i] && d1[n-i+7] && d2[n+i])	// 判断第n行第i列的位置是否危险
		{
			//宣布占领状态
			place[n] = i;		// 记录皇后的位置 
			flag[i] = 0;		// 记录第i列已经有皇后了 
			d1[n - i + 7] = 0;	// 记录这条上对角线是危险的 
			d2[n + i] = 0;		// 记录这条下对角线是危险的

			if (n < 7)			// 判断八个皇后放完了没有 
			{
				QueenVIII(n + 1);
			}
			else
			{
				output();		//输出
			}
			// 回溯
			flag[i]= 1;
			d1[n - i + 7] = 1;
			d2[n + i] = 1;
		}
	}
}

// 输出
void output(void)
{
	printf("第%d种解法：\n", ++key);
	for (int i = 0; i < 8; ++i)
	{
		for (int l = 0; l < 8; ++l)
		{
			if (place[i] == l)
			{
				printf("1 ");
			}
			else
			{
				printf("0 ");
			}
		}
		printf("\n");
	}
	printf("\n");
}