混合粒子群的混沌蝴蝶优化算法

一、理论基础

1、基本蝴蝶优化算法(BOA)

请参考这里。

2、基本粒子群优化算法(PSO)

请参考这里。

3、混合粒子群的混沌蝴蝶优化算法(HPSOBOA)

在这一部分中，提出了一种新的混合算法，引入了Cubic映射对BOA进行初始化，并采用了非线性参数控制策略。此外，将粒子群优化算法与BOA算法相结合，改进了基本的BOA算法，使其能够很好地进行全局优化。

（1）Cubic映射

混沌是非线性系统中比较常见的现象。基本Cubic映射可计算如下：$$z_{n+1}=\alpha z_n^3-\beta z_n\text{\hspace{1em}(1)}$$其中，$\alpha$和$\beta$表示混沌因子，当$\beta \in (2.3,3)$时，Cubic映射是混沌的。当$\alpha =1$时，Cubic映射序列值在$(-2,2)$之间； 当$\alpha =2$时，序列值在$(-1,1)$之间。Cubic映射也可表示为：$$z_{n+1}=\rho z_n(1-z_n^2)\text{\hspace{1em}(2)}$$其中，$\rho$为控制参数。在式(2)中，Cubic映射序列值在$(0,1)$之间，并且当$\rho =2.595$时生成的混沌变量具有更好的遍历性。图1显示了1000次迭代下的Cubic映射序列分布情况。

（a）混沌分岔

（b）混沌映射 图1 Cubic映射序列值分布

在图1中可以看出，混沌映射可以在搜索阶段将蝴蝶种群分布到$(0,1)$内的随机值。
为了保证初始值在$(0,1)$内，该算法将Cubic映射的$z(0)$设置为0.315。

（2）非线性参数控制策略

在基本BOA中，$a=0.1$无法有效平衡算法全局和局部搜索能力。因此，提出了一种非线性参数控制策略：$$a(t)=a_{first}-(a_{first}-a_{final})\cdot \sin (\frac{\pi }{\mu }(\frac{t}{T_{\max }}{)}^2)\text{\hspace{1em}(3)}$$其中，$a_{first}$和$a_{final}$分别表示参数$a$的初始值和最终值，$\mu$为调谐参数，$T_{\max }$表示最大迭代次数。在本文中，$\mu =2$，$T_{\max }=500$，$a_{first}=0.1$，$a_{final}=0.3$。
从图2可以看出，对于参数$a$，本文提出的基于正弦函数的非线性控制策略在早期阶段具有较大的斜率，这可以加快算法的全局探索能力；中期斜率减小，倾向于局部开发；后期坡度较缓，允许算法搜索最优解。因此，它可以有效地平衡算法的全局搜索和局部搜索能力。

图2 两种控制参数策略对比

（3）混合PSO的BOA算法(HPSOBOA)

为了结合这两种算法的优点，我们利用这两种算法的功能，而不是孤立地使用这两种算法。换句话说，由于生成两种算法的最终结果所涉及的方法不同，因此它是异构的。混合算法的数学模型如下：$$V_i^{t+1}=w\cdot V_i^t+C_1\cdot r_1\times (p_{best}-X_i^t)+C_2\cdot r_2\times (g_{best}-X_i^t)\text{\hspace{1em}(4)}$$$$w=w^{\max }-\frac{(w^{\max }-w^{\min })\cdot T_i}{T_{\max }}\text{\hspace{1em}(5)}$$其中，$C_1=C_2=0.5$，$w^{\max }=0.9$，$w^{\min }=0.2$，$r_1$和$r_2$为$(0,1)$的随机数。$$X_i^{t+1}=X_i^t+V_i^{t+1}\text{\hspace{1em}(6)}$$HPSOBOA的全局搜索阶段可表述如下：$$X_i^{t+1}=w\cdot X_i^t+(r^2\times g_{best}-w\cdot X_i^t)\times f_i\text{\hspace{1em}(7)}$$HPSOBOA的局部搜索阶段可表述如下：$$X_i^{t+1}=w\cdot X_i^t+(r^2\times X_k^t-w\cdot X_j^t)\times f_i\text{\hspace{1em}(8)}$$其中，$X_k^t$和$X_j^t$分别是从蝴蝶种群中随机选择的第$k$个和第$j$个个体。

（4）HPSOBOA算法伪代码

为了结合本文提出的三种改进策略的优点，本节提出了一种HPSOBOA算法，它是初始种群的Cubic映射、幂指数$a$的非线性参数控制策略、PSO算法和BOA的组合。HPSOBOA的伪代码如下图所示。

图3 HPSOBOA算法伪代码

二、仿真实验与结果分析

为了验证HPSOBOA的性能，将其与BOA、GWO、MPA和PSOBOA进行对比，设置种群规模为30，最大迭代次数为500，变量维数为100，每种算法独立运行30次，以文献[1]中F1、F3、F11、F19、F23、F25为例，结果显示如下：

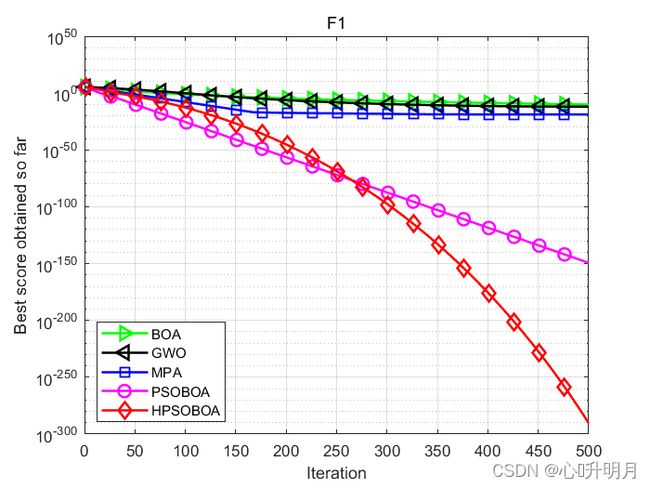
函数：F1
BOA：最差值: 1.0478e-10, 最优值: 6.827e-11, 平均值: 8.5373e-11, 标准差: 9.1295e-12, 秩和检验: 3.0199e-11
GWO：最差值: 2.7543e-12, 最优值: 1.9774e-13, 平均值: 1.1477e-12, 标准差: 7.1768e-13, 秩和检验: 3.0199e-11
MPA：最差值: 7.9029e-19, 最优值: 2.4073e-21, 平均值: 1.5296e-19, 标准差: 1.6315e-19, 秩和检验: 3.0199e-11
PSOBOA：最差值: 6.9971e-150, 最优值: 1.5725e-150, 平均值: 4.1598e-150, 标准差: 1.5452e-150, 秩和检验: 3.0199e-11
HPSOBOA：最差值: 5.0657e-291, 最优值: 1.3586e-291, 平均值: 3.4665e-291, 标准差: 0, 秩和检验: 1
函数：F3
BOA：最差值: 8.5762e-11, 最优值: 5.071e-11, 平均值: 7.0891e-11, 标准差: 7.5767e-12, 秩和检验: 3.0199e-11
GWO：最差值: 5327.5486, 最优值: 16.674, 平均值: 831.3783, 标准差: 1123.4146, 秩和检验: 3.0199e-11
MPA：最差值: 62.0811, 最优值: 0.008634, 平均值: 7.4039, 标准差: 11.7316, 秩和检验: 3.0199e-11
PSOBOA：最差值: 3.291e-148, 最优值: 1.6576e-149, 平均值: 1.3776e-148, 标准差: 9.3966e-149, 秩和检验: 3.0199e-11
HPSOBOA：最差值: 9.0269e-291, 最优值: 2.9765e-293, 平均值: 2.3786e-291, 标准差: 0, 秩和检验: 1
函数：F11
BOA：最差值: 9.2633e-11, 最优值: 6.3128e-11, 平均值: 7.7696e-11, 标准差: 7.4387e-12, 秩和检验: 3.0199e-11
GWO：最差值: 6.1597e-12, 最优值: 3.2253e-13, 平均值: 2.0634e-12, 标准差: 1.3049e-12, 秩和检验: 3.0199e-11
MPA：最差值: 4.7577e-19, 最优值: 1.243e-20, 平均值: 1.0014e-19, 标准差: 1.0248e-19, 秩和检验: 3.0199e-11
PSOBOA：最差值: 3.1816e-148, 最优值: 6.8402e-150, 平均值: 8.0738e-149, 标准差: 6e-149, 秩和检验: 3.0199e-11
HPSOBOA：最差值: 1.726e-290, 最优值: 6.0496e-294, 平均值: 4.5759e-291, 标准差: 0, 秩和检验: 1
函数：F19
BOA：最差值: 6.0445e-09, 最优值: 2.7618e-10, 平均值: 1.7392e-09, 标准差: 1.4347e-09, 秩和检验: 3.0199e-11
GWO：最差值: 0.0094119, 最优值: 0.00054518, 平均值: 0.004253, 标准差: 0.0020408, 秩和检验: 3.0199e-11
MPA：最差值: 1.3555e-11, 最优值: 3.0428e-14, 平均值: 3.2039e-12, 标准差: 2.9902e-12, 秩和检验: 3.0199e-11
PSOBOA：最差值: 6.6447e-75, 最优值: 9.9565e-76, 平均值: 3.8125e-75, 标准差: 1.4796e-75, 秩和检验: 3.0199e-11
HPSOBOA：最差值: 7.93e-146, 最优值: 7.6783e-148, 平均值: 2.2684e-146, 标准差: 1.7789e-146, 秩和检验: 1
函数：F23
BOA：最差值: 74.2999, 最优值: 56.9055, 平均值: 66.0232, 标准差: 3.8495, 秩和检验: 3.0199e-11
GWO：最差值: 40.4395, 最优值: 21.3662, 平均值: 28.3439, 标准差: 4.3098, 秩和检验: 3.0199e-11
MPA：最差值: 14.9872, 最优值: 4.2534, 平均值: 9.679, 标准差: 2.6916, 秩和检验: 2.8716e-10
PSOBOA：最差值: 89.6292, 最优值: 59.0824, 平均值: 80.8961, 标准差: 6.8158, 秩和检验: 3.0199e-11
HPSOBOA：最差值: 11.3602, 最优值: 0.11664, 平均值: 2.0446, 标准差: 2.1448, 秩和检验: 1
函数：F25
BOA：最差值: 0.89556, 最优值: 0.39798, 平均值: 0.41637, 标准差: 0.090528, 秩和检验: 3.0199e-11
GWO：最差值: 1.5919, 最优值: 0.39798, 平均值: 0.89878, 标准差: 0.29035, 秩和检验: 3.0199e-11
MPA：最差值: 0.39798, 最优值: 0.099496, 平均值: 0.23879, 标准差: 0.15146, 秩和检验: 1.9724e-06
PSOBOA：最差值: 0.10062, 最优值: 5.5341e-140, 平均值: 0.049859, 标准差: 0.050711, 秩和检验: 0.00039881
HPSOBOA：最差值: 0.10306, 最优值: 4.4157e-291, 平均值: 0.0268, 标准差: 0.045206, 秩和检验: 1

实验结果表明：HPSOBOA算法可有效提升基本BOA的收敛速度和寻优精度。

三、参考文献

[1] Zhang, M., Long, D., Qin, T., et al. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems[J]. Symmetry, 2020, 12(11): 1800.