机器学习十大经典算法
机器学习算法是计算机科学和人工智能领域的关键组成部分,它们用于从数据中学习模式并作出预测或做出决策。本文将为大家介绍十大经典机器学习算法,其中包括了线性回归、逻辑回归、支持向量机、朴素贝叶斯、决策树等算法,每种算法都在特定的领域发挥着巨大的价值。
1 线性回归
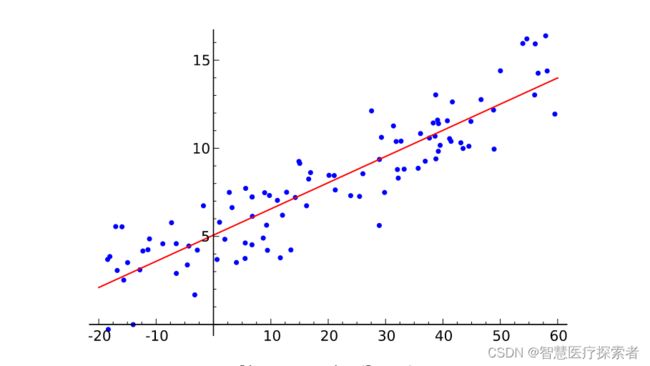
线性回归算得上是最流行的机器学习算法之一,它是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,目前线性回归的运用十分广泛。线性回归就是要找一条直线,并且让这条直线尽可能地拟合散点图中的数据点。它试图通过将直线方程与该数据拟合来表示自变量(x 值)和数值结果(y 值)。然后就可以用这条线来预测未来的值!这种算法最常用的技术是最小二乘法。这个方法计算出最佳拟合线,以使得与直线上每个数据点的垂直距离最小。总距离是所有数据点的垂直距离(绿线)的平方和。其思想是通过最小化这个平方误差或距离来拟合模型。
算法详细讲解:机器学习之线性回归模型
2 逻辑回归
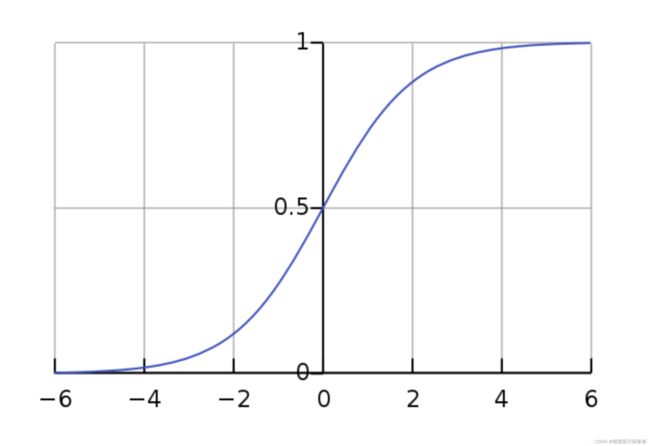
逻辑回归(Logistic regression)与线性回归类似,但它是用于输出为二进制的情况(即,当结果只能有两个可能的值)。对最终输出的预测是一个非线性的 S 型函数,称为 logistic function, g()。
这个逻辑函数将中间结果值映射到结果变量 Y,其值范围从 0 到 1。然后,这些值可以解释为 Y 出现的概率。S 型逻辑函数的性质使得逻辑回归更适合用于分类任务。
算法详细讲解:机器学习之逻辑回归
3 K近邻算法
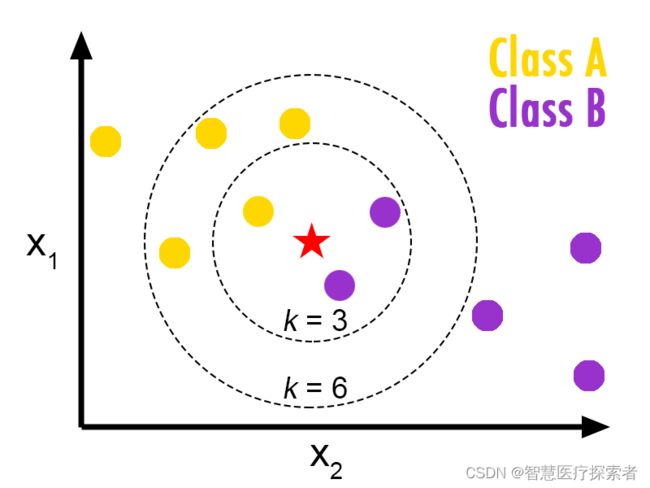
K- 最近邻算法(K-Nearest Neighbors,KNN)非常简单。KNN 通过在整个训练集中搜索 K 个最相似的实例,即 K 个邻居,并为所有这些 K 个实例分配一个公共输出变量,来对对象进行分类。
K 的选择很关键:较小的值可能会得到大量的噪声和不准确的结果,而较大的值是不可行的。它最常用于分类,但也适用于回归问题。
用于评估实例之间相似性的距离可以是欧几里得距离(Euclidean distance)、曼哈顿距离(Manhattan distance)或明氏距离(Minkowski distance)。欧几里得距离是两点之间的普通直线距离。它实际上是点坐标之差平方和的平方根。
算法详细讲解:机器学习之K紧邻算法
4 K-均值算法
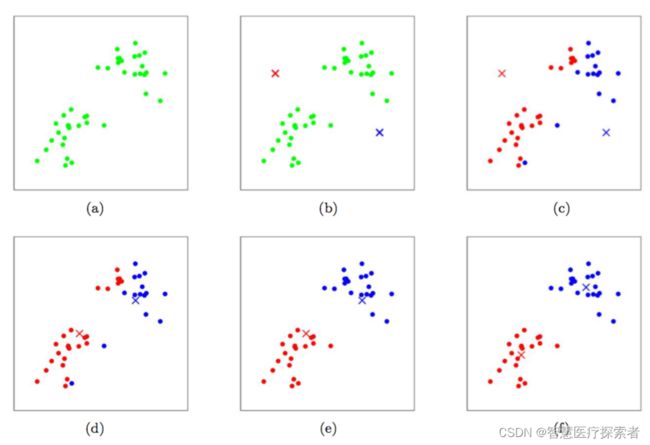
K- 均值(K-means)是通过对数据集进行分类来聚类的。例如,这个算法可用于根据购买历史将用户分组。它在数据集中找到 K 个聚类。K- 均值用于无监督学习,因此,我们只需使用训练数据 X,以及我们想要识别的聚类数量 K。
该算法根据每个数据点的特征,将每个数据点迭代地分配给 K 个组中的一个组。它为每个 K- 聚类(称为质心)选择 K 个点。基于相似度,将新的数据点添加到具有最近质心的聚类中。这个过程一直持续到质心停止变化为止。
算法详细讲解:机器学习之K-均值算法
5 支持向量机
支持向量机(support vector machine,SVM)是有监督学习中最有影响力的机器学习算法之一,该算法的诞生可追溯至上世纪 60 年代, 前苏联学者 Vapnik 在解决模式识别问题时提出这种算法模型,此后经过几十年的发展直至 1995 年, SVM 算法才真正的完善起来,其典型应用是解决手写字符识别问题。
SVM 是一种非常优雅的算法,有着非常完善的数学理论基础,其预测效果,在众多机器学习模型中“出类拔萃”。在深度学习没有普及之前,“支持向量机”可以称的上是传统机器学习中的“霸主”。
支持向量机是一种二分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。支持向量机的学习算法是求解凸二次规划的最优化算法。
算法详细讲解:机器学习之支持向量机
6 朴素贝叶斯
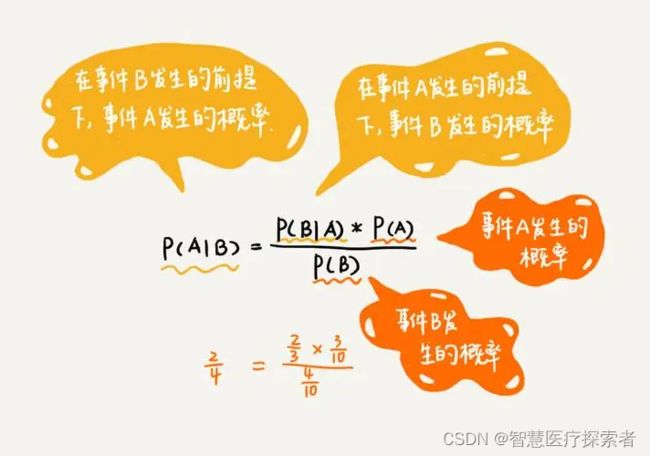
朴素贝叶斯是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率,是应用最为广泛的分类算法之一。
朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
朴素贝叶斯对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
算法详细讲解:机器学习之朴素贝叶斯
7 决策树
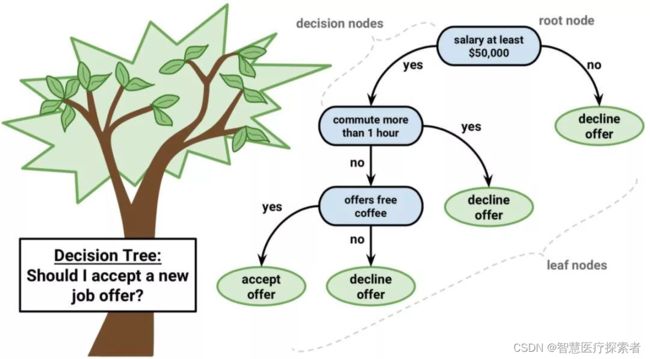
决策树(Decision Tree,又称为判定树)算法是机器学习中常见的一类算法,是一种以树结构形式表达的预测分析模型。决策树属于监督学习(Supervised learning),根据处理数据类型的不同,决策树又为分类决策树与回归决策树。最早的的决策树算法是由Hunt等人于1966年提出,Hunt算法是许多决策树算法的基础,包括ID3、C4.5和CART等。
决策树可用于回归和分类任务。在这一算法中,训练模型通过学习树表示(Tree representation)的决策规则来学习预测目标变量的值。树是由具有相应属性的节点组成的。在每个节点上,我们根据可用的特征询问有关数据的问题。左右分支代表可能的答案。最终节点(即叶节点)对应于一个预测值。每个特征的重要性是通过自顶向下方法确定的。节点越高,其属性就越重要。
算法详细讲解:机器学习之决策树
8 随机森林
随机森林(Random Forest)是一种非常流行的集成机器学习算法。这个算法的基本思想是,许多人的意见要比个人的意见更准确。在随机森林中,我们使用决策树集成。为了对新对象进行分类,我们从每个决策树中进行投票,并结合结果,然后根据多数投票做出最终决定。
随机森林算法由于其良好的性能和可解释性,适用于许多不同的应用场景。在分类问题、回归问题、特征选择、异常检测等多种场景中发挥重要作用。
算法详细讲解:机器学习之随机森林
9 主成分分析
主成分分析(Principal Component Analysis)简称PCA,是一个非监督学习的机器学习算法,主要用于数据的降维,对于高维数据,通过降维,可以发现更便于人类理解的特征。
PCA是实现数据降维的一种算法。正如其名,假设有一份数据集,每条数据的维度是D,PCA通过分析这D个维度的前K个主要特征(这K个维度在原有D维特征的基础上重新构造出来,且是全新的正交特征),将D维的数据映射到这K个主要维度上进而实现对高维数据的降维处理。 PCA算法所要达到的目标是,降维后的数据所损失的信息量应该尽可能的少,即这K个维度的选取应该尽可能的符合原始D维数据的特征。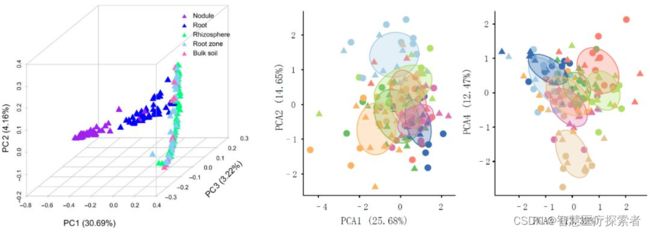
算法详细讲解:机器学习之主成分分析
10 Boosting和AdaBoost
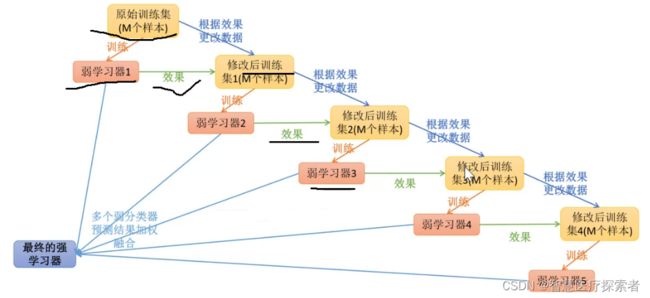
Boosting 是一种试图利用大量弱分类器创建一个强分类器的集成技术。要实现 Boosting 方法,首先你需要利用训练数据构建一个模型,然后创建第二个模型(它企图修正第一个模型的误差)。直到最后模型能够对训练集进行完美地预测或加入的模型数量已达上限,我们才停止加入新的模型。
AdaBoost 是第一个为二分类问题开发的真正成功的 Boosting 算法。它是人们入门理解 Boosting 的最佳起点。当下的 Boosting 方法建立在 AdaBoost 基础之上,最著名的就是随机梯度提升机。
算法详细讲解:机器学习之Boosting和AdaBoos