ResNet（残差网络）详解

      ResNet在《Deep Residual Learning for Image Recognition》论文中提出，是在CVPR 2016发表的一种影响深远的网络模型，由何凯明大神团队提出来，在ImageNet的分类比赛上将网络深度直接提高到了152层，前一年夺冠的VGG只有19层。ImageNet的目标检测以碾压的优势成功夺得了当年识别和目标检测的冠军，COCO数据集的目标检测和图像分割比赛上同样碾压夺冠，可以说ResNet的出现对深度神经网络来说具有重大的历史意义。论文下载地址：地址，有兴趣的小伙伴可以阅读原文。

一、没有出现ResNet之前

      神经网络越深的卷积层理论上可以提取更多的图像特征，但是事实结果并不是，如下图：

                                                        该图是作则在CIFAR-10上做的测试数据；左侧是训练接结果，右侧是测试集结果

       

        从图中可以看出错误率在20层时候是最低的，添加到了56层反而更高了。可能会有小伙伴说是不是过拟合了？其实可以看出来，如果是过你过拟合的话，左侧的训练接在56层时候的错误率依然上升，所以并不是过拟合产生的该情况，是由于神经网络在反向传播过程中通过链式法则不断地反向传播更新梯度，而当网络层数加深时，梯度在传播过程中会逐渐消失也就说我们所说的梯度弥散。这将导致无法对前面网络层的权重进行有效的调整，网络层数越深，训练误差越高，导致训练和测试效果变差，这一现象称为退化。那么，理论上本应该层次更深、效果更好的神经网络，实验结果反而不好，该怎么解决这个问题呢？很多学者都为此感到头疼，幸好RestNet姗姗赶来。

二、ResNet网络解析

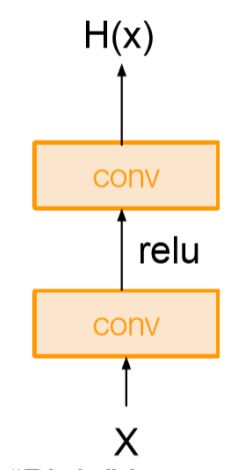
       传统的平原网络如下图所示，这是一个普通的、两层的卷积+激活。

                                                                    

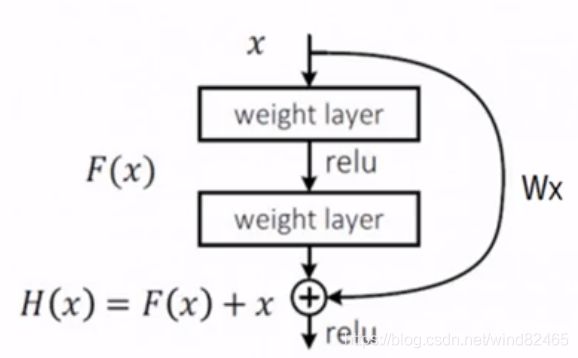
        经过两层卷积+一个激活，我们假定它输出为H(x)。与传统的网络结构相比，ResNet增加了“短路”连接(shortcut connection)或称为跳跃连接(skip connection) ，如下图所示：

                          

        它添加了一个短路连接到第二层激活函数之前。那么激活函数的输入就由原来的输出H(x)=F(x)变为了H(x)=F(x)+x。在RestNet中，这种输出=输入的操作成为恒等映射。那么，上图中的identity其实功能也是恒等映射。

        那么这么做的好处是什么呢？在深度神经网络中，随着训练过程中反向传播权重参数的更新，网络中某些卷积层已经达到最优解了，其实此时这些层的输入输出都是一样的，已经没有训练的必要。但实际训练过程中，我们是很难将权重参数训练为绝对0误差的，但是这种情况已经是最优解了，其实对这些层的训练过程是可以抛弃的，即此时可以设F(x)=0，那么这时的输出为H(x)=x就是最优输出。

        在传统平原网络中，即未加入identity之前，如果网络训练已经达到最优解了，那么随着网络继续训练、权重参数的更新，有可能将已经达到最优解的权重参数继续更新为误差更多的值。但随着identity的加入，在达到最优解的时候直接通过F(x)=x,那么权重参数可以达到至少不会比之前训练效果差的目的，并且可以加快网络收敛。

       在解决梯度弥散的问题上，其实可以通过如下的公式分析：

                                                            

        上面的公式中，现有网络的某个深层的卷积层，表示某个残差的输入层，可以看出在残差网络中，下面的层次残差的块的输出都可以由上面的某一层确定。

在反向传播中，残差网络的梯度公式求带后如下所示：

                                                   

      可以看出，反向传播的梯度由2项组成，对x的直接映射，梯度为1；为多层普通神经网络映射上的结果。

即使新增的多层神经网络的梯度为0时残差网络的梯度更新多了一个“1”！就是我们之前定义的identity这条路径，正是由于多了这条捷径，来自深层的梯度能直接畅通无阻地通过，去到上一层，使得浅层的网络层参数等到有效的训练，避免了梯度消失问题。

 那么，现在我们可以展示一下残差网络整体模型结构。将平原网络修改为残差网络后的网络结构如下所示：

                                                                                      

        从上图中可以看到每两个卷积层就添加了一个“短路”连接。实现就是我们的直连identity shortcuts。但是有些网络中，F(x)和x的维度不一致，此时我们需要做一下为杜转换，上图的虚线就是我们带有维度操作的残差块，如下所示就是带有卷积操作的残差块。

                                                       

       这种情况下，我们原有残差公式由H(x)=F(x)+x，变为H(x)=F(x)+*x。

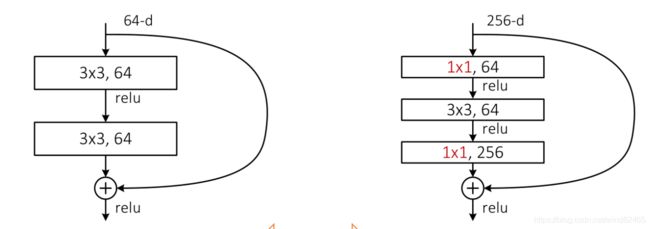
       以上就是残差网络的详细解释。对于50层以上的深度网络模型，何凯明团队还设计了多用1×1的卷积层，减少了网络参数，如下图所示：

       

       上图可以看出，针对层次较多的网络，将原有的两个3×3卷积变为了1×1、3×3和1×1的卷积。 在ResNet50、ResNet101和ResNet152中都是用了该结构设计。

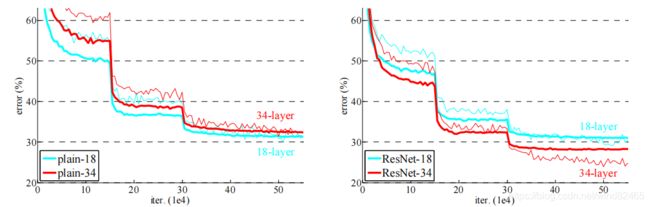
       最后附上论文中残差网络的实验结果。

    

      可以看出右面34层的的检测效果明显更好。