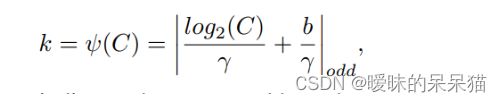注意力模块

 目前主流的注意力机制可以分为以下三种：通道注意力、空间注意力以及自注意力（Self-attention）

• 通道域旨在显示的建模出不同通道之间的相关性，通过网络学习的方式来自动获取到每个特征通道的重要程度，最后再为每个通道赋予不同的权重系数，从而来强化重要的特征抑制非重要的特征。
• 空间域旨在提升关键区域的特征表达，本质上是将原始图片中的空间信息通过空间转换模块，变换到另一个空间中并保留关键信息，为每个位置生成权重掩膜（mask）并加权输出，从而增强感兴趣的特定目标区域同时弱化不相关的背景区域。（以CBAM代表）
• 混合域主要是共同结合了通道域、空间域等注意力的形式来形成一种更加综合的特征注意力方法。

一、ECA 注意力模块
ECA 注意力模块，它是一种通道注意力模块；常常被应用与视觉模型中。支持即插即用，即：它能对输入特征图进行通道特征加强，而且最终ECA模块输出，不改变输入特征图的大小。

背景：ECA-Net认为：SENet中采用的降维操作会对通道注意力的预测产生负面影响；同时获取所有通道的依赖关系是低效的，而且不必要的；
设计：ECA在SE模块的基础上，把SE中使用全连接层FC学习通道注意信息，改为1*1卷积学习通道注意信息；通过 一维卷积 layers.Conv1D 来完成跨通道间的信息交互，卷积核的大小通过一个函数来自适应变化，使得通道数较大的层可以更多地进行跨通道交互。
作用：使用1*1卷积捕获不同通道之间的信息，避免在学习通道注意力信息时，通道维度减缩；降低参数量；（FC具有较大参数量；1*1卷积只有较小的参数量）
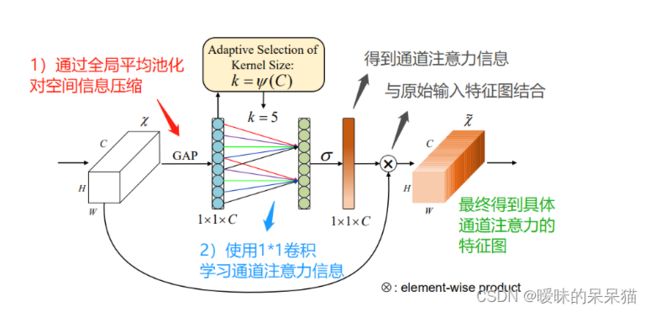
模块的结构：

 ECA模型的流程思路如下:

• 首先输入特征图，它的维度是H*W*C；
• 对输入特征图进行空间特征压缩；实现：在空间维度，使用全局平均池化GAP，得到1*1*C的特征图；
• 对压缩后的特征图，进行通道特征学习；实现：通过1*1卷积，学习不同通道之间的重要性，此时输出的维度还是1*1*C；
• 最后是通道注意力结合，将通道注意力的特征图1*1*C、原始输入特征图H*W*C，进行逐通道乘，最终输出具有通道注意力的特征图。

FC全连接层时，对输入的通道特征图处理，是进行全局学习的；

如果使用1*1卷积，只能学习到局部的通道之间的信息；

在做卷积操作时，它的卷积核大小，会影响到感受野；为解决不同输入特征图，提取不同范围的特征时，ECA使用了动态的卷积核，来做1*1卷积，学习不同通道之间的重要性。

• 动态卷积核是指：卷积核的大小通过一个函数来自适应变化；
• 在通道数较大的层，使用较大的卷积核，做1*1卷积，使得更多地进行跨通道交互；
• 在通道数较小的层，使用较小的卷积核，做1*1卷积，使得较少地进行跨通道交互；
   

 卷积和自适应函数，定义如下：

  其中k表示卷积核大小；C表示通道数；| |odd表示k只能取奇数；和b表示在论文中设置为2和1,用于改变通道数C和卷积核大小和之间的比例。

# --------------------------------------------------------- #
#（2）ECANet 通道注意力机制
# 使用1D卷积代替SE注意力机制中的全连接层
# --------------------------------------------------------- #
 
import torch
from torch import nn
import math
from torchstat import stat  # 查看网络参数
 
# 定义ECANet的类
class eca_block(nn.Module):
    # 初始化, in_channel代表特征图的输入通道数, b和gama代表公式中的两个系数
    def __init__(self, in_channel, b=1, gama=2):
        # 继承父类初始化
        super(eca_block, self).__init__()
        
        # 根据输入通道数自适应调整卷积核大小
        kernel_size = int(abs((math.log(in_channel, 2)+b)/gama))
        # 如果卷积核大小是奇数，就使用它
        if kernel_size % 2:
            kernel_size = kernel_size
        # 如果卷积核大小是偶数，就把它变成奇数
        else:
            kernel_size = kernel_size
        
        # 卷积时，为例保证卷积前后的size不变，需要0填充的数量
        padding = kernel_size // 2
        
        # 全局平均池化，输出的特征图的宽高=1
        self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
        # 1D卷积，输入和输出通道数都=1，卷积核大小是自适应的
        self.conv = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=kernel_size,
                              bias=False, padding=padding)
        # sigmoid激活函数，权值归一化
        self.sigmoid = nn.Sigmoid()
    
    # 前向传播
    def forward(self, inputs):
        # 获得输入图像的shape
        b, c, h, w = inputs.shape
        
        # 全局平均池化 [b,c,h,w]==>[b,c,1,1]
        x = self.avg_pool(inputs)
        # 维度调整，变成序列形式 [b,c,1,1]==>[b,1,c]
        x = x.view([b,1,c])
        # 1D卷积 [b,1,c]==>[b,1,c]
        x = self.conv(x)
        # 权值归一化
        x = self.sigmoid(x)
        # 维度调整 [b,1,c]==>[b,c,1,1]
        x = x.view([b,c,1,1])
        
        # 将输入特征图和通道权重相乘[b,c,h,w]*[b,c,1,1]==>[b,c,h,w]
        outputs = x * inputs
        return outputs

二 、SENet
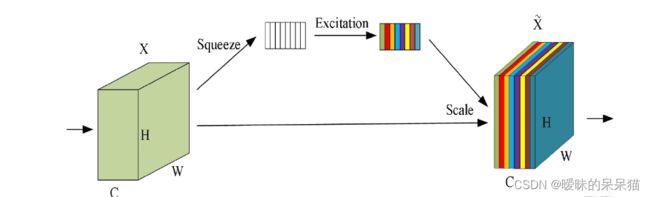
SE注意力机制（Squeeze-and-Excitation Networks）在通道维度增加注意力机制，关键操作是squeeze和excitation。

通过自动学习的方式，使用另外一个新的神经网络，获取到特征图的每个通道的重要程度，然后用这个重要程度去给每个特征赋予一个权重值，从而让神经网络重点关注某些特征通道。提升对当前任务有用的特征图的通道，并抑制对当前任务用处不大的特征通道。

如下图所示，在输入SE注意力机制之前（左侧图C），特征图的每个通道的重要程度都是一样的，通过SENet之后（右侧彩图C），不同颜色代表不同的权重，使每个特征通道的重要性变得不一样了，使神经网络重点关注某些权重值大的通道。

SE注意力机制的实现步骤如下：

• （1）Squeeze：通过全局平均池化，将每个通道的二维特征（H*W）压缩为1个实数，将特征图从 [h, w, c] ==> [1,1,c]
• （2）excitation：给每个特征通道生成一个权重值，论文中通过两个全连接层构建通道间的相关性，输出的权重值数目和输入特征图的通道数相同。[1,1,c] ==> [1,1,c]
• （3）Scale：将前面得到的归一化权重加权到每个通道的特征上。论文中使用的是乘法，逐通道乘以权重系数。[h,w,c]*[1,1,c] ==> [h,w,c]

 总结：

1. SENet的核心思想是通过全连接网络根据loss损失来自动学习特征权重，而不是直接根据特征通道的数值分配来判断，使有效的特征通道的权重大。当然SE注意力机制不可避免的增加了一些参数和计算量，但性价比还是挺高的。
2. 论文认为excitation操作中使用两个全连接层相比直接使用一个全连接层，它的好处在于，具有更多的非线性，可以更好地拟合通道间的复杂关联。

# -------------------------------------------- #
#（1）SE 通道注意力机制
# -------------------------------------------- #
import torch
from torch import nn
from torchstat import stat  # 查看网络参数
 
# 定义SE注意力机制的类
class se_block(nn.Module):
    # 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接下降通道的倍数
    def __init__(self, in_channel, ratio=4):
        # 继承父类初始化方法
        super(se_block, self).__init__()
        
        # 属性分配
        # 全局平均池化，输出的特征图的宽高=1
        self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
        # 第一个全连接层将特征图的通道数下降4倍
        self.fc1 = nn.Linear(in_features=in_channel, out_features=in_channel//ratio, bias=False)
        # relu激活
        self.relu = nn.ReLU()
        # 第二个全连接层恢复通道数
        self.fc2 = nn.Linear(in_features=in_channel//ratio, out_features=in_channel, bias=False)
        # sigmoid激活函数，将权值归一化到0-1
        self.sigmoid = nn.Sigmoid()
        
    # 前向传播
    def forward(self, inputs):  # inputs 代表输入特征图
    
        # 获取输入特征图的shape
        b, c, h, w = inputs.shape
        # 全局平均池化 [b,c,h,w]==>[b,c,1,1]
        x = self.avg_pool(inputs)
        # 维度调整 [b,c,1,1]==>[b,c]
        x = x.view([b,c])
        
        # 第一个全连接下降通道 [b,c]==>[b,c//4]
        x = self.fc1(x)
        x = self.relu(x)
        # 第二个全连接上升通道 [b,c//4]==>[b,c]
        x = self.fc2(x)
        # 对通道权重归一化处理
        x = self.sigmoid(x)
        
        # 调整维度 [b,c]==>[b,c,1,1]
        x = x.view([b,c,1,1])
        
        # 将输入特征图和通道权重相乘
        outputs = x * inputs
        return outputs

 构造输入层，查看一次前向传播的输出结果，打印网络结构

# 构造输入层shape==[4,32,16,16]   #4维tensor，各参数含义：[width, height, channels, kernel_nums]
inputs = torch.rand(4,32,16,16)
# 获取输入通道数
in_channel = inputs.shape[1]
# 模型实例化
model = se_block(in_channel=in_channel)
 
# 前向传播查看输出结果
outputs = model(inputs)
print(outputs.shape)  # [4,32,16,16])
 
print(model) # 查看模型结构
stat(model, input_size=[32,16,16])  # 查看参数，不需要指定batch维度

三.空洞卷积

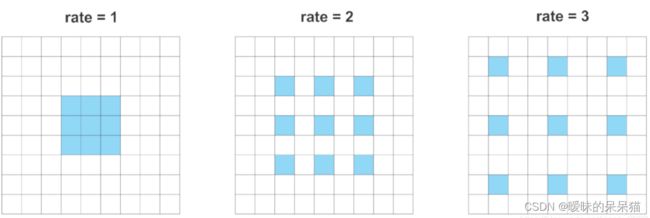
 普通的卷积：

 空洞卷积：

 空洞卷积（Atrous Convolution）是 DeepLab 模型的关键之一，它可以在不改变特征图大小的同时控制感受野，这有利于提取多尺度信息。空洞卷积如下图所示，其中rate（r）控制着感受野的大小，r 越大感受野越大。通常的 CNN 分类网络的 output_stride=32，若希望 DilatedFCN 的 output_stride=16，只需要将最后一个下采样层的 stride 设置为1，并且后面所有卷积层的 r 设置为 2，这样保证感受野没有发生变化。对于 output_stride=8，需要将最后的两个下采样层的 stride 改为 1，并且后面对应的卷积层的 rate 分别设为 2 和 4。另外一点，DeepLabv3 中提到了采用 multi-grid 方法，针对 ResNet 网络，最后的 3 个级联 block 采用不同 rate，若 output_stride=16 且 multi_grid = (1, 2, 4), 那么最后的 3 个 block 的 rate= 2 · (1, 2, 4) = (2, 4, 8)。这比直接采用 (1, 1, 1) 要更有效一些，不过结果相差不是太大。