第六章代码题（二）

4.三叉链表存储的结构的二叉树，结点的数据域和孩子域已经填好内容，编写算法给双亲域填上指向其双亲的指针。

三叉链表就是比二叉链表的结构多了一个双亲域

 结构体：

//三叉链表的存储结构
typedef struct TNode {
	ElemType data;
	struct TNode* Lchild;
	struct TNode* Rchild;
	struct TNode* Parent;
}TiTnode,*TiTree;

 该题思路其实很简单，方法参数为两个结点类型的指针，ttree用来进行遍历当前结点，pre总是为前一个访问的结点。 注意根节点肯定没有双亲结点，所以可以将pre初始化为空。每次调用该方法如果当前结点不为空，让当前结点的双亲域等于前一个访问的结点即可。

答案：

//第四题 三叉链表存储结构找双亲指针
void SearchParent(TiTree ttree,TiTnode *pre) {

	//结点为空，直接进行返回
	if (ttree==NULL)
	{
		return ;
	}
	ttree->Parent = pre;

	SearchParent(ttree->Lchild, ttree);
	SearchParent(ttree->Rchild, ttree);
}

验证：

因为创建了新的结构类型，所以在之前的验证的二叉树遍历函数的参数结构类型和给二叉树添加结点函数的参数结构类型改成新结构体的类型。除此之外为了更直观的展示函数结果，写一个专门输出每个结点的双亲域的值的函数。代码如下：

//展示每个三叉链表存储的二叉树的双亲域的值
int showParent(TiTree ttree) {
	if (ttree==NULL)
	{
		return 0;
	}
	if (ttree->Parent!=NULL)
	{
		printf("\n%d的双亲结点是%d", ttree->data, ttree->Parent->data);
	}
	
	showParent(ttree->Lchild);
	showParent(ttree->Rchild);
}

 主函数：

int main() {
	TiTree ttree = NULL;
	TiTnode* pre = NULL;
	for (int i = 0; i < MaxSize; i++)
	{
		ttree = AddNode_T(ttree, rand() % 100 + 1);
	}
	printf("\n中序遍历\n");
	MiddleTraversal(ttree);
	printf("\n前序遍历\n");
	BeforeTraversal(ttree);
	SearchParent(ttree,pre);
	showParent(ttree);
	
	return 0;
}

执行结果：

画出该二叉树：

 

 5.不使用递归和栈的先序遍历线索二叉树

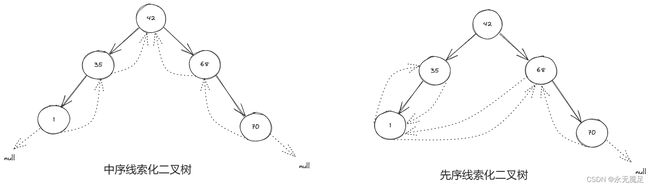
首先要了解线索化二叉树，简单来说就是在原有的二叉树的结构上面增加一个左标识域和一个右标识域。如图：

代码结构：

/*线索二叉树的定义*/
typedef struct CLTNode {
	ElemType data;
	//标识域，为0时指向各自对应的孩子，为1时指向各自对应的遍历前驱和后继
	int ltag, rtag;			
	struct CLTNode* lchild, * rchild;
} CLTNode, * CLTree;

为了后续验证方便，先做一个中序遍历线索二叉树。如果能写出来中序，那么先序也就很好写了。

线索化的函数里面包括两个参数，一个就是二叉树类型的变量p,另外一个就是指向指针的指针变量pre，p指的是遍历的当前结点，pre指的是遍历前一个访问的结点。

由前面可以知道线索化的二叉树，左标识域为1时，左孩子域存的是遍历的前驱，同样地，右孩子域在右标识域为1时，存的就是遍历的后继。

所以判定条件有两个，当前结点没有左孩子时，就要存前驱，它的前驱就是遍历前一个访问的结点；另外一个就是当pre不为空且其右孩子为空时，就要存后继，它的后继就是当前结点。

两个递归就根据不同遍历来确定位置，比如中序遍历就应该先找到最左下的结点，先序遍历则是先直接进行判定。

这里要注意的是，pre初始应该赋值为空，原因很简单，中序遍历最左下的结点的左孩子一定为空，但是它是中序遍历的第一个结点，那么它的前驱应该为空。其次在判定pre时，必须要判定pre是否为空，否则会报空指针错误。

还有就是pre的类型，和第三题一样，它应该是指向前驱结点指针的指针。有关二叉树的函数最大的特点就是递归，也就是在函数里面调用函数本身，所以如果只是传递一个前驱结点的指针，在递归调用时，传递进去的只是这个指针的副本而不是本身，这样在回溯的过程中pre实际的地址并不会发生改变，导致无法正确的建立线索化的关系。简单来说就是值传递和引用传递。

//第五题  二叉树线索化(中序)
void Inthread(CLTree p,CLTNode **pre) {
	//如果当前结点存在
	if (p) {
		Inthread(p->lchild,pre);//递归当前结点的左子树，进行线索化
		//如果当前结点没有左孩子，左标志位设为1，左指针域指向上一结点 pre
		if (p->lchild==NULL) {
			p->ltag = 1;
			p->lchild = *pre;
		}
		//如果 pre 没有右孩子，右标志位设为 1，右指针域指向当前结点。
		if (*pre!=NULL && (*pre)->rchild==NULL) {
			(*pre)->rtag = 1;
			(*pre)->rchild = p;
		}
		*pre = p;//线索化完左子树后，让pre指针指向当前结点
		Inthread(p->rchild,pre);//递归右子树进行线索化
	}
}

 进行遍历：

//中序遍历线索二叉树
void InOrderThraverse_Thr(CLTree cltree)
{
    while (cltree)
    {
        //一直找左孩子，最左下边的结点就是中序遍历的第一个结点

        while (cltree->ltag == 0) {
            cltree = cltree->lchild;
        }

        printf("%d ", cltree->data);  

        //当结点右标志位为1时，直接找到其后继结点
        while (cltree->rtag == 1 && cltree->rchild != NULL) {
            cltree = cltree->rchild;
            printf("%d ", cltree->data);
        }

        //否则，按照中序遍历的规律，找其右子树中最左下的结点，也就是继续循环遍历
        cltree = cltree->rchild;
    }
}

接下来完成这道题，先序线索化二叉树就是把中序线索化二叉树里面的代码顺序换一下：

这里要注意先序递归时比中序多了判定条件，不加判定条件就会陷入无限循环当中最终导致报错栈溢出。因为前面先进行了线索化，原本为空的孩子域就会指向遍历的前驱或后继。如果不判定直接进行递归，便会陷入无限循环。

代码：

//二叉树先序线索化
void BeforeInthread(CLTree p, CLTNode** pre) {
	//如果当前结点存在
	if (p) {

		//如果当前结点没有左孩子，左标志位设为1，左指针域指向上一结点 pre
		if (p->lchild == NULL) {
			p->ltag = 1;
			p->lchild = *pre;
		}
		//如果 pre 没有右孩子，右标志位设为 1，右指针域指向当前结点。
		if (*pre != NULL && (*pre)->rchild == NULL) {
			(*pre)->rtag = 1;
			(*pre)->rchild = p;
		}
		*pre = p;//线索化该结点后，让pre指针指向当前结点
		if (p->ltag==0)
		{
			BeforeInthread(p->lchild, pre);//递归当前结点的左子树，进行线索化
		}
		if (p->rtag==0)
		{
			BeforeInthread(p->rchild, pre);//递归右子树进行线索化
		}
	
	}
}

遍历：

//先序遍历线索二叉树
void InOrderThraverse_Before(CLTree cltree)
{
	//根据先序遍历直接进行输出
	printf("%d ", cltree->data);  
	while (cltree)
	{
		if (cltree->ltag==0&&cltree->lchild!=NULL)
		{
			cltree = cltree->lchild;
		}
		printf("%d ", cltree->data);
		while ( cltree->rtag==1 && cltree->rchild!=NULL)
		{
			cltree = cltree->rchild;
			printf("%d ", cltree->data);
		}
		cltree = cltree->rchild;
	}
}

验证：

验证的时候要注意，不同的遍历对应的线索二叉树也不同，中序遍历的应该是中序线索化的二叉树，先序遍历的应该是先序线索化的二叉树。 分别进行一次线索化和遍历。

中序：

int main() {
CLTree cltree = NULL;
	CLTNode* p = NULL;

	for (int  i = 0; i < MaxSize; i++)
	{
		cltree = AddNode_CL(cltree, rand()%100 + 1);
	}
	Inthread(cltree, &p);
	printf("遍历中序线索二叉树");
	InOrderThraverse_Thr(cltree);

	return 0;
}

 执行结果：

先序：

int main() {
CLTree cltree = NULL;

	for (int  i = 0; i < MaxSize; i++)
	{
		cltree = AddNode_CL(cltree, rand()%100 + 1);
	}
	CLTNode* q = NULL;
	BeforeInthread(cltree, &q);
	printf("遍历先序线索二叉树");
	InOrderThraverse_Before(cltree);

	return 0;
}

执行结果：

 二叉树的先序线索化和中序线索化如图：