GAMES101-现代计算机图形学入门
GAMES101-现代计算机图形学入门
Lecture 01 : Overview of Computer Graphics
主要内容:
1.什么是计算机图形学
2.计算机图形学的应用
3.课程主要内容:光栅化,曲线和曲面,光线追踪,动画和模拟
• What is Computer Graphics?
计算机图形学是一种使用数学算法将二维或三维图形转化为计算机显示器的栅格形式的科学。简单地说,计算机图形学的主要研究内容就是研究如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法。
Applications
1.Video Games
2.Movies
3.Animations
4.Design
5.Visualization
6.Virtual Reality
7.Augmented Reality
8.Digital Illustration
9.Simulation
10.Graphical User Interfaces
11.Typography
• Course Topics
Rasterization
Project geometry primitives (3D triangles / polygons) onto the screen
什么是光栅化?
光栅化是将几何数据经过一系列变换后最终转换为像素,从而呈现在显示设备上的过程。光栅化的本质是坐标变换、几何离散化。
Curves and Meshes
How to represent geometry in Computer Graphics
Ray Tracing
Shoot rays from the camera though each pixel
Calculate intersection and shading
Continue to bounce the rays till they hit light sources
Animation / Simulation
Lecture 2:Review of Linear Algebra
主要内容:
1.线性代数基本内容:向量和矩阵的运算
Vectors
什么是向量:既有大小又有方向的量
Vector Normalization
单位向量:模(长度)是1的向量,用于表示一个方向。向量单位化用向量除以向量的模。
Vector Addition
Geometrically: Parallelogram law & Triangle law
Algebraically: Simply add coordinates
向量怎么相加:几何中,用三角形法则,平行四边形法则。代数中直接两个坐标相加。
Cartesian Coordinates
平面直角坐标系中的向量表示
A=3 * X+4 * Y
方便计算。
Vector Multiplication
Dot product
几何中: a * b = | a | * | b | * cos
在平面直角坐标系中 a * b= xa * bx + ya * yb
结果是一个数字
满足交换律,结合律,分配律。
可以通过点乘求两个向量的夹角
可以求出一个向量在另一个向量上的投影
可以判断两个向量有多么接近,相同方向,相反方向,垂直。
Cross product
Cross product is orthogonal to two initial vectors
Direction determined by right-hand rule
Useful in constructing coordinate systems (later)
叉积结果是一个向量,方向用右手螺旋定则判断
a x b = - b x a
| a x b | = | a | * | b | sin
不满足交换律
a x a = 0向量
可以用叉积构建三维中的坐标系
叉积可以判断向量是在左还是在右,在里还是在外,若 a x b > 0 则b在a的左侧, a x b < 0 则在右侧
判断一个点是否在三角形内,判断点是否同时在三条边的左边或右边即可,在边上时自己说了算。
Matrices
什么是矩阵:纵横排列的二维数据表格。
Matrix-Matrix Multiplication
矩阵加法。
矩阵乘法:
( M x N ) ( N x P) = ( M x P )
相乘的结果中,第i行第j列的元素等于第一个矩阵的第i行的行向量与第二个矩阵的第j列的列向量点乘的结果。
不满足交换律
转置矩阵
( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
单位矩阵,矩阵的逆
( A B ) − 1 = B − 1 A − 1 (AB)^-1=B^-1A^-1 (AB)−1=B−1A−1
向量的点乘和叉乘都可以转换成矩阵乘法
Lecture 3:Transformation
主要内容:
1.2D变换:旋转,缩放,切变
2.齐次坐标
3.组合变换
Today
Why study transformation
Modeling
Viewing
模型变换,视图变换
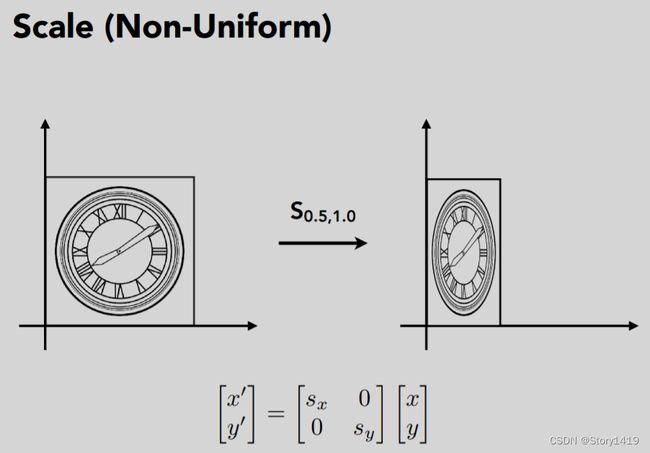
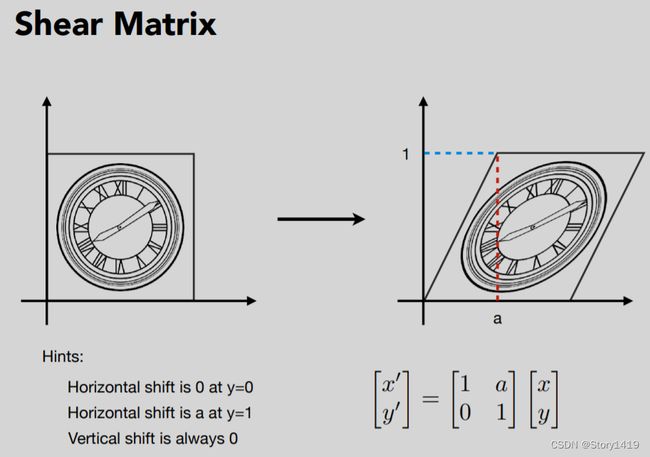
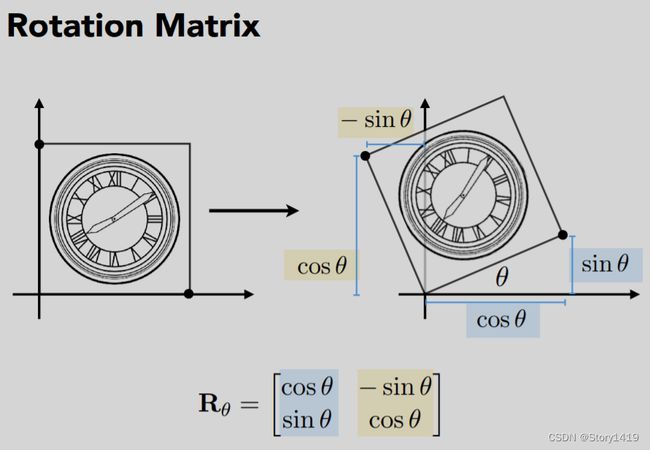
2D transformations: rotation, scale, shear
Representing transformations using matrices
Homogeneous coordinates
为什么要引入齐次坐标:因为平移的矩阵表示不属于矩阵的线性变换,希望能有一种统一的变换方式。




乘上逆矩阵等于做一个逆变换。
Composing transforms
任意操作的变换都可以由几个简单的变换组合而成,且变换的顺序不同,结果也不同,因为矩阵乘法不满足交换律,最终结果也不同。
变换的顺序从右往左,即要把先执行的变换放到式子的右边。
因为矩阵乘法满足结合律,所以可以把变换的左边都先乘起来,得到一个3x3的矩阵,该矩阵包含了很多次操作。
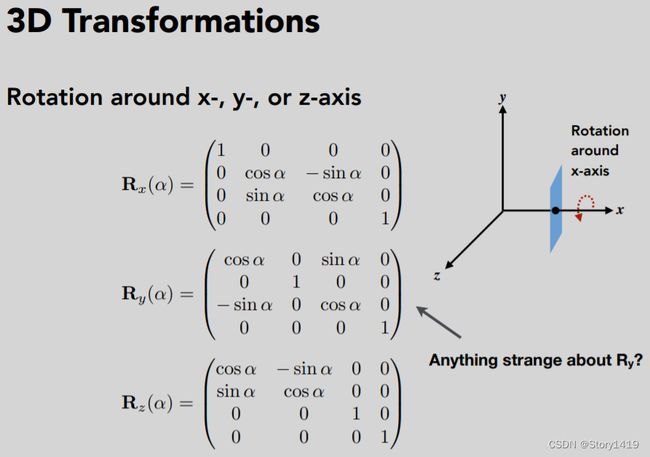
3D Transforms
Lecture 4:Transformation Cont.
主要内容:
1.3D变换
2.MVP变换:模型变换,视图变换,投影变换。
3.投影变换:正交投影,透视投影
Viewing (观测) transformation
View (视图) / Camera transformation
视图变换
What is view transformation?
Think about how to take a photo
Find a good place and arrange people (model transformation)
Find a good “angle” to put the camera (view transformation)
Cheese! (projection transformation)
简称MVP变换
How to perform view transformation?
Define the camera first.
Position e,Look-at / gaze direction g,Up direction t (assuming perp. to look-at)
相机总是在原点,看向e方向,向上的方向是t,把相机归位时让其他物体也跟着一起变换,看到的图是一样的
Projection (投影) transformation
投影变换
Orthographic (正交) projection
一种简单的理解方式:相机在原点,看向-z,上面为y轴,然后扔掉z轴,然后缩放到[-1,1]x[-1,1]
In general
We want to map a cuboid [l, r] x [b, t] x [f, n] to the “canonical (正则、规范、标准)” cube [-1, 1]^3
因为相机始终面向-z,所以约近(n)的z值就越大,越远(f)的z值就越小。在左手系中不一样。
Perspective (透视) projection
First “squish” the frustum into a cuboid (n -> n, f -> f) (Mpersp->ortho)
Do orthographic projection (Mortho, already known!)
先压缩成一个标准长方形,再做一次正交投影
Lecture 5:Rasterization 1 (Triangles)
主要内容:
1.透视投影中视锥的定义
2.像素定义
3.光栅化
4.一些光栅设备
5.采样,走样
Rasterization
Different raster displays
Rasterizing a triangle
透视投影中,定义屏幕的长宽比和垂直角度,就可以表示一个视锥。
MVP变换之后,就把结果画在屏幕上
What is a screen?
An array of pixels
Size of the array: resolution
A typical kind of raster display
Raster == screen in German
Rasterize == drawing onto the screen
Pixel (FYI, short for “picture element”)
For now: A pixel is a little square with uniform color
Color is a mixture of (red, green, blue)
屏幕上由很多密集的像素,假设每个像素都只有一个颜色。
像素在二维数组的坐标都是整数,(0, 0) 到(width - 1, height - 1),每个像素的中心都是x+0.5,y+0.5,屏幕的范围则是(0, 0) 到(width, height)
Triangles - Fundamental Shape Primitives
Why triangles?
Most basic polygon
Break up other polygons
Unique properties
Guaranteed to be planar
Well-defined interior
Well-defined method for interpolating values at vertices over triangle (barycentric interpolation)
多边形都可以拆成很多个三角形,三角形的内外划分明确,方便定义插值,是最基础的多边形。
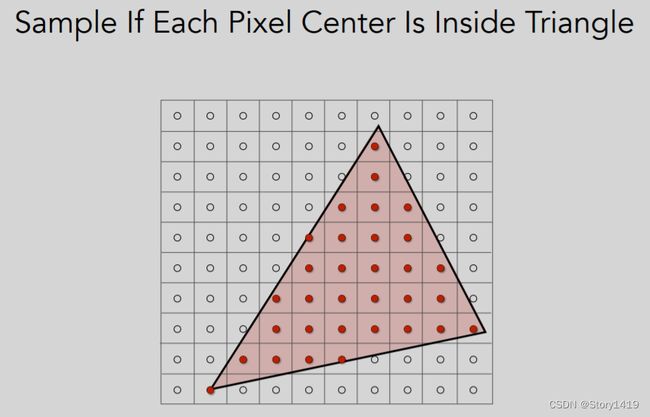
A Simple Approach: Sampling
光栅化的一个简单方法:采样
当像素中心在三角形上时,由自己规定可在里面或外面。
会出现走样(锯齿)的问题。Aliasing (Jaggies)
Lecture 6:Rasterization 2 (Antialiasing and Z-Buffering)
主要内容:
1.采样,走样,反走样
Antialiasing
Sampling theory
Antialiasing in practice
Artifacts due to sampling - “Aliasing”
Jaggies – sampling in space
Moire – undersampling images
Wagon wheel effect – sampling in time
[Many more] …
走样:用同一种采样方式采样不同频率的函数,得到的结果无法区分,这就叫走样。在频率的角度上来说,就是频谱在复制粘贴情况下,发生了混合
锯齿,摩尔纹,车轮效应等走样现象。
Behind the Aliasing Artifacts
Signals are changing too fast (high frequency), but sampled too slowly
信号变化太快,而采样太慢跟不上造成的。
先模糊再采样可以做到反走样
Convolution Theorem
Convolution in the spatial domain is equal to multiplication in the frequency domain, and vice versa
Option1:
Filter by convolution in the spatial domain
Option2:
Transform to frequency domain (Fourier transform)
Multiply by Fourier transform of convolution kernel
Transform back to spatial domain (inverse Fourier)
卷积定理。在时域中卷积等于在频域中乘积
Option 1: Increase sampling rate
Essentially increasing the distance between replicas in the Fourier domain
Higher resolution displays, sensors, framebuffers…
But: costly & may need very high resolution
Option 2: Antialiasing
Making Fourier contents “narrower” before repeating
i.e. Filtering out high frequencies before sampling
如何减少走样?
方法1:增加采样率
方法2:采样前过滤高频率
那么如何模糊呢:MSAA,每个像素内部分成四个小像素,分别判断是否在三角形里,以此来估计该像素颜色的比例。不是通过增加采样率。实际中用不规则的分布。
Lecture 7:Shading 1 (Illumination, Shading and Graphics Pipeline)
主要内容:
1.深度缓存
2.着色
Visibility / occlusion
Z-buffering
Shading
Illumination & Shading
Graphics Pipeline
Painter’s Algorithm:Paint from back to front, overwrite in the framebuffer
画家算法:先画最远的图像,再画最近的图像,近的图像会挡住远的图像
当涉及到三个面互相遮挡时不适用。由此引出深度缓冲
Z-Buffer
Idea:
Store current min. z-value for each sample (pixel)
Needs an additional buffer for depth values
frame buffer stores color values
depth buffer (z-buffer) stores depth
IMPORTANT: For simplicity we suppose z is always positive (smaller z -> closer, larger z -> further)
每个三角形光栅化成像素之后,每个像素点都只记录离屏幕最近的信息,最后再显示出来。
简单起见,我们认为z都是正数,且越近的z越小,越远的z越大
Z-Buffer Algorithm
Initialize depth buffer to ∞
During rasterization:
for(each triangle T)
for(each sample(x,y,z) in T)
if (z < zbuffer[x,y]) // closest sample so far
framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z; // update depth
else
; // do nothing, this sample is occluded
先把所有像素都初始化成无穷大,即无穷远
对于每一个三角形,考虑其中的每一个像素,记录最近的像素的信息。
时间复杂度O(n)
Shading:The process of applying a material to an object
着色,给物体用材质的过程
一个简单的着色模型:Blinn-Phong Reflectance Model
分为高光,漫反射,环境光
漫反射公式:Ld = kd (I/r^2)*max(0, n · l)
Lecture 8:Shading 2 (Shading, Pipeline and Texture Mapping)
主要内容:
1.Blinn-Phong reflectance model 的镜面反射和环境光
2.图像渲染管线
3.纹理映射
Shading 2
Blinn-Phong reflectance model
Specular and ambient terms
Shading frequencies
Graphics pipeline
Intensity depends on view direction
Bright near mirror reflection direction
光的强度取决于反射的方向,观测的方向越接近镜面反射的方向越能看到高光
半程向量 h = bisector(v, l) 光和视线的向量相加后归一,就是半程向量,它与法线越接近,越高光
Ls = ks (I/r^2) max(0, n · h)^p
当角度移动很小时,希望高光变化剧烈,所以加上指数p用于控制。p越大高光的范围越小。
环境光:La = ka*Ia
环境光从任何地方看都一样,与法线和光线方向无关,这里认为环境光是一个常量。
Blinn-Phong 着色模型
L = La + Ld + Ls = ka Ia + kd (I/r2) max(0, n · l) + ks (I/r2) max(0, n · h) p
着色频率:
Flat shading:用每个三角面的法向量着色
Gouraud shading:用三角面的三个顶点的法向量着色
Phong shading:利用三角面的三个顶点的法向量,插值出三角面离的所有像素的法向量,来着色。
顶点的法向量怎么求?
一个简单的方法:用共用这个点的三角面的法向量求平均,就是或者顶点的法向量。
Graphics (Real-time Rendering) Pipeline
如何从一个场景到一张图,中间经历了什么样的过程,这个过程就叫管线。
Texture Mapping
纹理映射:可以直接认为,一张2d的纹理上记录了3d物体中的坐标,相当于把它贴上去。
在着色的时候希望一个面上的着色能有不同的颜色等属性,可以用纹理去规定相关的属性,改变颜色就是改变公式前面的k
Lecture 9:Shading 3 (Texture Mapping cont.)
主要内容:
1.重心坐标–用于插值
2.纹理放大问题
Shading 3
Barycentric coordinates
Texture queries
Applications of textures
Interpolation Across Triangles: Barycentric Coordinates
(x, y) = aA + bB+cC
a+b+c=1
重心坐标:平面中的任何一个点都可以用三角形三个顶点的坐标的线性组合表示,且系数a+b+c=1,当三个系数都>=0时点在三角形内。
Texture Magnification
纹理放大
一张小纹理贴到很大的屏幕上时,纹理会被拉大,纹理里的一个像素变大,则屏幕的很多个小的像素会映射到纹理的同一个像素上,形成锯齿。
Bilinear Interpolation
用双线性插值可以让结果变好
纹理变小
纹理过大时,纹理被压缩变小,屏幕上一个像素对应纹理里很多变化细节,无法很好表示出来,也会出现锯齿。一个像素内,它的频率很高,就会出现走样。
增加采样率就可以解决,但是开销大。
可以不采样,立刻知道这片区域的平均值就好了
范围查询问题
Mipmap
Allowing (fast, approx., square) range queries
可以范围查询,很快,近似,只能是正方形。
在计算机视觉中也叫图像金字塔
只是多了1/3的存储量。
由于Mipmap每层之间是离散的,为了让变化更平滑,查询中间连续的层,一次再插值一次
Trilinear Interpolation
三线性插值
但是还是有问题,因为只能查询正方形的平均值,所以远处的会出现Overblur的现象。
对于一个长条,任然用正方形取近似,就会出错。
Anisotropic Filtering
各向异性过滤
只能用矩形查询,但斜着的仍没有解决
EWA filtering
一个大的图拆成很多个小的图去查询,多次查询。
Lecture 10:Geometry 1 (Introduction)
主要内容:
1.纹理的应用
2.几何的表示:隐式–距离函数。显示。
Applications of textures
Introduction to geometry (2nd part of this course!)
Examples of geometry
Various representations of geometry
纹理可以表示环境光,用一个球记录环境光,极点会有扭曲的情况,可以用一个立方体,记录六个面,但不利于查询
凹凸贴图(法线贴图)
纹理可以定义凹凸或者说法线,这样就可以影响着色的效果。
可以在不加入更多三角形的情况下增加更多表面细节
Displacement mapping
位移贴图:与法线贴图相比,它真的改变了三角形的顶点的位置,更加逼真。
缺点:要求三角形得足够细致
纹理也可以是三维的。
纹理可以存储各种信息,等到要用的时候直接乘上使用,比如阴影和颜色,之后看在着色器里如何解释它。
几何
集合有很多种不同的表示方式
Implicit
algebraic surface
level sets
distance functions
…
Explicit
point cloud
polygon mesh
subdivision, NURBS
隐式几何:
点满足特定的关系,则认为点在某个平面上,比如x2+y2+z2 = 1,推广,f(x,y,z) = 0
判断面上有哪些点很难,图像很难想象,但很方便判断一个点是否在面上,面内或面外,
任何复杂的几何都可以用简单的几何通过布尔运算表达出来
距离函数:空间中任何一个点到物体表面的最小距离,两个物体的距离函数融合在一起再恢复,可以做出水滴的效果
在表面之外,距离函数为正,在表面之内,距离函数为负。
距离函数可以表示光滑过度的几何形体,表示能力很强
Fractals
分形:自相似
显示几何
所有点直接给出,或者使用参数映射的方式给出,一个平面的点映射到三维空间的一个点
但是判断点是否在面上,面内,面外很难。
Lecture 11:Geometry 2 (Curves and Surfaces)
主要内容:
1.曲线:贝塞尔曲线
2.曲面
Explicit Representations
Curves
Bezier curves
De Casteljau’s algorithm
B-splines, etc.
Surfaces
Bezier surfaces
Triangles & quads
Subdivision, simplification, regularization
几何的显示表示有很多种:
1.point clouds,点云:把物体用很密集的点表示出来。最简单的表示方法,很容易表示任何远远大于一个点的几何,通常转换成多边形面
2.Polygon Mesh,多边形面:用三角面或四边形面表示,容易处理,模拟,但需要更复杂的数据结构,是目前最广泛的应用
Curves
曲线
Bézier Curves (⻉塞尔曲线):是由一系列**控制点(Control Point)**所定义的一条平滑曲线
de Casteljau Algorithm
可以直接用一个公式计算
n+1个点算出最终n阶的点,就是以伯恩斯坦多项式作为系数,对各个点加权的结果。
⻉塞尔曲线的性质:t等于0和1时一定在两个端点上,与端点段相切,仿射变换前后的曲线相通,但投影之后不一定
符合凸包性质:形成的曲线一定在控制点形成的凸包内
Piecewise Bézier Curves
逐段的⻉塞尔曲线
控制点多的时候结果不直观。
目前应用最多的是用四个控制点画一段曲线,就像ps里的钢笔工具一样。
连续性:
只要第一个曲线的重点是第二个曲线的起点,就是C0连续
共点的两个切线斜率相同且长度相同,就是C1连续
其他曲线:Spline,样条
B-splines
Surfaces
曲面
贝塞尔曲面